The diagram below shows part of the graph where
.
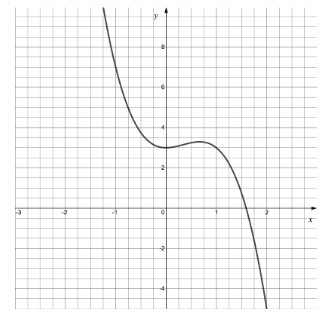
(i) Find
(ii) Find
Write down an interval, in the form , such that
, explain clearly your choice of values for a and b.
Did this page help you?
Exam code: H240
The diagram below shows part of the graph where
.

(i) Find
(ii) Find
How did you do?
Write down an interval, in the form , such that
, explain clearly your choice of values for a and b.
How did you do?
Did this page help you?
A solution to the equation is
, correct to two significant figures.
(i) Write down the lower bound, l, and the upper bound, u, of 3.1.
(ii) Assuming is continuous in the interval
, what can you say about the values of
and
?
How did you do?
Did this page help you?
Show that the equation can be rewritten as
How did you do?
Starting with , use the iterative formula
to find values for and
, giving each to four decimal places where appropriate.
How did you do?
Did this page help you?
The functionis defined as
Use the sign change rule to show there is a root, , of
in the interval
.
How did you do?
(i) Find
(ii) Show that, in this instance, the Newton-Raphson method would be given by the iteration
How did you do?
(i) Use the Newton-Raphson method with to find values of
and
, giving each to five decimal places.
(ii) Use your answers to part (i) to estimate to the highest degree of accuracy possible.
How did you do?
Did this page help you?
The diagram below shows part of the graph with equation .
The trapezium rule is to be used to estimate the shaded area of the graph which is given by the integral
(i) Given that 4 strips are to be used, calculate the width of each strip, h.
(ii) Complete the table of values below, giving each entry correct to three significant figures.
x | 1 | 1.25 | 1.5 | 1.75 | 2 |
y | 3.90 |
|
| 4.48 |
|
(iii) Use the trapezium rule with the values from the table in part (ii) to find an estimate of the shaded area.
How did you do?
Did this page help you?
The graph of where
is shown below. θ is measured in radians and -

Given that .
(i) Find and
.
(ii) Explain how, in this case, the change of sign rule fails to locate a root of in the interval (1.5 , 1.6).
How did you do?
Did this page help you?
A student is trying to find a solution to the equation using an iterative formula.
The student rearranges into the form
.
The diagram below shows a sketch of the graphs of and
.

The student is trying to find the root , starting with an initial estimate
. Show on the diagram, how the iterative formula will converge and find the root
. Mark the
-axis with the positions of
and
.
How did you do?
Did this page help you?
The diagram below shows part of the graph with equation .

The trapezium rule is to be used to estimate the shaded area of the graph which is given by the integral
(i) All of the values in the table below will be used in the trapezium rule. Write down the number of ordinates that will be used, the number of strips and the width of each strip. x 4 5 6 7 8 9 10 y 1.59 2.08 2.52 2.92 3.30 3.70 4.00
(ii) Apply the trapezium rule, using the values above, to find an estimate of the shaded area.
(iii) State, with a reason, whether your answer to part (ii) is an over-estimate or an under-estimate.
How did you do?
Did this page help you?
The diagram below shows part of the graph where

(i) Find and
, giving your answers to three significant figures.
(ii) Briefly explain the significance of your results from part (i).
How did you do?
One of the solutions to the equation is
, correct to three significant figures.
(i) Write down the upper and lower bound of 2.55.
(ii) Hence, use the sign change rule to confirm that this is a solution (to three significant figures) to the equation .
How did you do?
Did this page help you?
Show that the equation can be rewritten as
How did you do?
Starting with , use the iterative formula
to find a root of the equation , correct to two decimal places.
How did you do?
Did this page help you?
The function is defined as
Use the sign change rule to show there is a root to the equation in the interval
.
How did you do?
Find .
How did you do?
Use the Newton-Raphson method with to find the root in the interval
correct to three decimal places.
How did you do?
Did this page help you?
The diagram below shows part of the graph with equation .

The trapezium rule is to be used to estimate the shaded area of the graph which is given by the integral.
Given that 4 strips are to be used, calculate h, the width of each strip.
How did you do?
Complete the table of values below, giving each entry correct to three significant figures.
x | 5 | 6.25 | 7.5 | 8.75 | 10 |
y | 3.05 |
| 4.04 |
|
|
How did you do?
Find an estimate of the shaded area using the values from the table in part (b).
How did you do?
State whether your answer to part (c) is an overestimate or an underestimate.
How did you do?
Did this page help you?
Part of the graph of is shown below, where
is measured in radians.
Explain why the change of sign rule would fail if attempting to locate a root of the function using the values of θ = 1.55 and θ = 1.65.
How did you do?
Did this page help you?
The diagram below shows the graphs of and
.

The iterative formula
is to be used to find an estimate for a root, , of the function
.
Write down an expression for .
How did you do?
Using an initial estimate, , show, by adding to the diagram above, which of the two points (S or T) the sequence of estimates
will converge to.
Hence deduce whether is the
-coordinate of point S or point T.
How did you do?
Find the estimates and
, giving each to three decimal places.
How did you do?
Confirm that α = 4.146 correct to three decimal places.
How did you do?
Did this page help you?
The diagram below shows the graph of ,
, where α and β are roots of the function
.

The Newton-Raphson method is to be used to estimate the values of α and β.
Draw a line on the diagram to indicate a starting value () that would lead the Newton-Raphson method to fail in finding either root. (It is not required that you state the value of
.)
How did you do?
Show that
How did you do?
Use the Newton-Raphson method with to find β correct to five significant figures.
How did you do?
Did this page help you?
The diagram below shows the graph with equation .

The area shaded is to be estimated using the trapezium rule where .
(i) Write down the number of strips to be used.
(ii) Write down the number of ordinates to be used.
How did you do?
Apply the trapezium rule as described above to estimate the shaded area, giving your answer to three significant figures.
How did you do?
Describe a way in which the estimate calculated in part (b) could be improved.
How did you do?
Did this page help you?
The diagram below shows part of the function where
.

Correct to three significant figures, and
.
Explain why using the sign change rule with these values would not necessarily be helpful in finding the root close to .
How did you do?
Using suitable values of x, show that there is a root close to .
How did you do?
Show that the root close to is 0.982, correct to three significant figures.
How did you do?
Did this page help you?
The diagram below shows a sketch of the graphs , and
.

An iterative formula is used to find roots to the equation .
On the diagram above show that the iterative formula
would converge to the root close to when using a starting value of
.
How did you do?
(i) Use in the iterative formula from part (a) to find three further approximations to the root close to
. Give each approximation correct to three significant figures.
(ii) Comment on your approximations and what they suggest about convergence to the root close to .
How did you do?
Confirm that the root close to is 3.49 correct to three significant figures.
How did you do?
Did this page help you?
The function is defined as
, where
is in radians.
Find .
How did you do?
Use the Newton-Raphson method with to find a root, α, of the equation
, correct to four decimal places.
How did you do?
The graph of has a local maximum point at
. Briefly explain why the Newton-Raphson method would fail if the exact value of β was used for
.
How did you do?
Did this page help you?
The diagram below shows part of the graph with equation

Use the trapezium rule with 5 strips to find an estimate for the shaded area, giving your answer to three significant figures.
How did you do?
Did this page help you?
The diagrams below show the graphs of four different functions.


Match each graph above with the correct statement below.
The sign change rule with values of and
would indicate a root but has failed due to the discontinuity (asymptote) at
.
The sign change rule with values of and
would indicate no root but has failed because there are two roots in the interval (1 , 5).
The sign change rule with values of and
would indicate no root but fail as there are two roots in the interval (3 , 5).
The sign change rule with values of and
would indicate no root but has failed to find the root as the graph has a turning point at
.
How did you do?
Did this page help you?
The diagram below shows the graphs of and
.

Show on the diagram, using the value of indicated, how an iterative process will lead to a sequence of estimates that converge to the x-coordinate of the point P. Mark the estimates
and
on your diagram.
How did you do?
By finding a suitable iterative formula, use to estimate a root to the equation
correct to two significant figures.
How did you do?
Confirm that your answer to part (b) is correct to two significant figures.
How did you do?
Did this page help you?
The diagram below shows part of the graph of where
.

Write down the x-coordiante of the point marked M on the graph.
How did you do?
The first two positive roots of the function , α and β, are marked on the graph above. The Newton-Raphson method is to be used to find a sequence of estimates for the root β.
Indicate on the graph above a value of in the interval (α , β) that would lead to the Newton-Raphson method converging to the root (i) α and (ii) β.
How did you do?
Using the Newton-Raphson method with , find four more estimates for the root β.
Verify that your final estimate gives the value of β correct to five significant figures.
How did you do?
Did this page help you?
Use two separate diagrams to show how the trapezium rule can lead to an underestimate or an overestimate when used to estimate the area under a curve.
How did you do?
Use the trapezium rule with to find an estimate for the area bounded by the curve with equation
, the lines with equations
and
and the x-axis.
Give your answer to three significant figures.
How did you do?
The integral
can be evaluated exactly by applying the method of integration by parts (twice). Suggest a reason why it may be preferrable to use a numerical method, such as trapezium rule, to estimate the integral rather than use integration by parts to find its exact value.
How did you do?
Did this page help you?
The diagram below shows the graph of where the function
is defined by

The function has a root close to
.
Using the iterative formula
with , find an estimate of the root near
to six decimal places
How did you do?
Given that, use the Newton-Raphson method with
to find an estimate of the root near
to six decimal places.
How did you do?
Justify which of the methods in this case was more efficient at finding the root close to to six decimal places.
How did you do?
Did this page help you?
Use the two diagrams below to show how rectangles can be used to give an upper and lower bound when estimating the area under a curve using the trapezium rule.


How did you do?
Did this page help you?
The diagram below shows part of the graph with equation .

A student searches for a root of the equation .
They find that and that
.
The student concludes that there is a root in the interval .
Explain why the student’s conclusion is incorrect.
How did you do?
Verify that is a solution to the equation
How did you do?
Explain why the sign change rule would fail if searching for the root of the equation
.
How did you do?
Did this page help you?
The function, is defined by
Show that the equation can be written in the form
How did you do?
On the same diagram sketch the graphs of and
.
How did you do?
The equation has a root, α, close to
.
The iterative formula xn+1=e-xn+1 with x0=2 is to be used to find correct to three significant figures.
Show, using a diagram and your answer to part (b), that this formula and initial x value will converge to the root α.
How did you do?
(i) Find the values ofand
, giving each correct to three significant figures.
(ii) How many iterations are required before and
agree to two decimal places?
How did you do?
The root lies in the interval .
Write down the values of p and q such that can be deduced accurate to two decimal places from the interval.
How did you do?
Did this page help you?
The function f(x) is defined as
Show that
How did you do?
Use the Newton-Raphson method with to find a root of the equation
correct to five significant figures.
How did you do?
Write down the exact value of a root to the equation .
How did you do?
Did this page help you?
The trapezium rule is to be used to find an estimate for the integral
The table below shows values for x and f(x), rounded to three significant figures where appropriate.
x | 4 | 4.5 | 5 | 5.5 | 6 | 6.5 | 7 | 7.5 | 8 |
f(x) | 3.16 | 3.39 | 3.61 | 3.81 | 4 | 4.18 | 4.36 | 4.53 | 4.69 |
Using the values in the table find
(i) an estimate for the integral using 2 strips,
(ii) an estimate for the integral using 4 strips,
(iii) an estimate for the integral using 8 strips.
How did you do?
Justify which of the estimates from part (a) will be the most accurate estimate for the integral.
How did you do?
Did this page help you?
Sketch three separate graphs with values of and
, to show how the sign change rule would fail to find a root α in the interval (p , q) for the following reasons:.
(i) Sign change rule indicates a root but there isn’t one due to a discontinuity in the graph.
(ii) Sign change rule indicates no root but there is a root at a turning point.
(iii) Sign change rule indicates no root but there are in fact two roots in the interval p , q.
On each diagram, clearly labelled p, q and the root α.
How did you do?
Did this page help you?
Sketch two separate diagrams to show how an iterative formula of the form can diverge in two different ways when being used to find an estimate for a root to the equation
.
How did you do?
Did this page help you?
Draw a diagram to show how the Newton-Raphson method produces a series of estimates that converge to a root, α. On your diagram you should indicate the values α, x0, x1 and x2.
How did you do?
Use the Newton-Raphson method with to find a solution to equation
correct to four significant figures.
How did you do?
Verify that there is another solution in the interval (0.605 , 0.615) and state the value of the root to the highest degree of accuracy possible.
How did you do?
Did this page help you?
The diagram below shows the graph of

Use the trapezium rule with h = 0.2 to find an estimate of the integral
to three significant figures.
How did you do?
Using the integration feature on your calculator, find the value of
Give your answer to three significant figures.
How did you do?
Assuming your calculator provides the exact answer to the integral, find the percentage error of your estimate from part (a).
How did you do?
Did this page help you?
The diagram below shows the graph of where the function
is defined by

The function f(x) has a root close to .
Estimates for this root could be found using iteration or the Newton-Raphson method.
(i) Suggest a suitable starting value for both methods.
(ii) Rearrange f(x) into the form
(iii) Find an expression for f '(x)
How did you do?
Using your answers to part (a) use an iterative method to find the root of close to
to four decimal places.
How did you do?
Using your answers to part (a) use the Newton-Raphson method to find the root of close to
to four decimal places.
How did you do?
Comment on the efficiency of the two methods in finding the root close to to four decimal places.
How did you do?
Did this page help you?
The diagram below shows a sketch of the graph of

The graph has a local maximum point at (2 , 32) as indicated on the diagram.
Use the trapezium rule with 5 ordinate values to estimate the area shaded.
How did you do?
Using the appropriate working values from part (a), find an upper and lower bound for the area shaded.
How did you do?
Suggest a reason why using the trapezium rule in this case is not appropriate.
How did you do?
Did this page help you?