Small Angle Approximations (OCR A Level Maths A) : Revision Note
Did this video help you?
Small Angle Approximations
Small angle approximations
When an angle measured in radians is very small, you can approximate the value using small angle approximations
These only apply when angles are measured in radians
They can be applied to positive and negative small angles
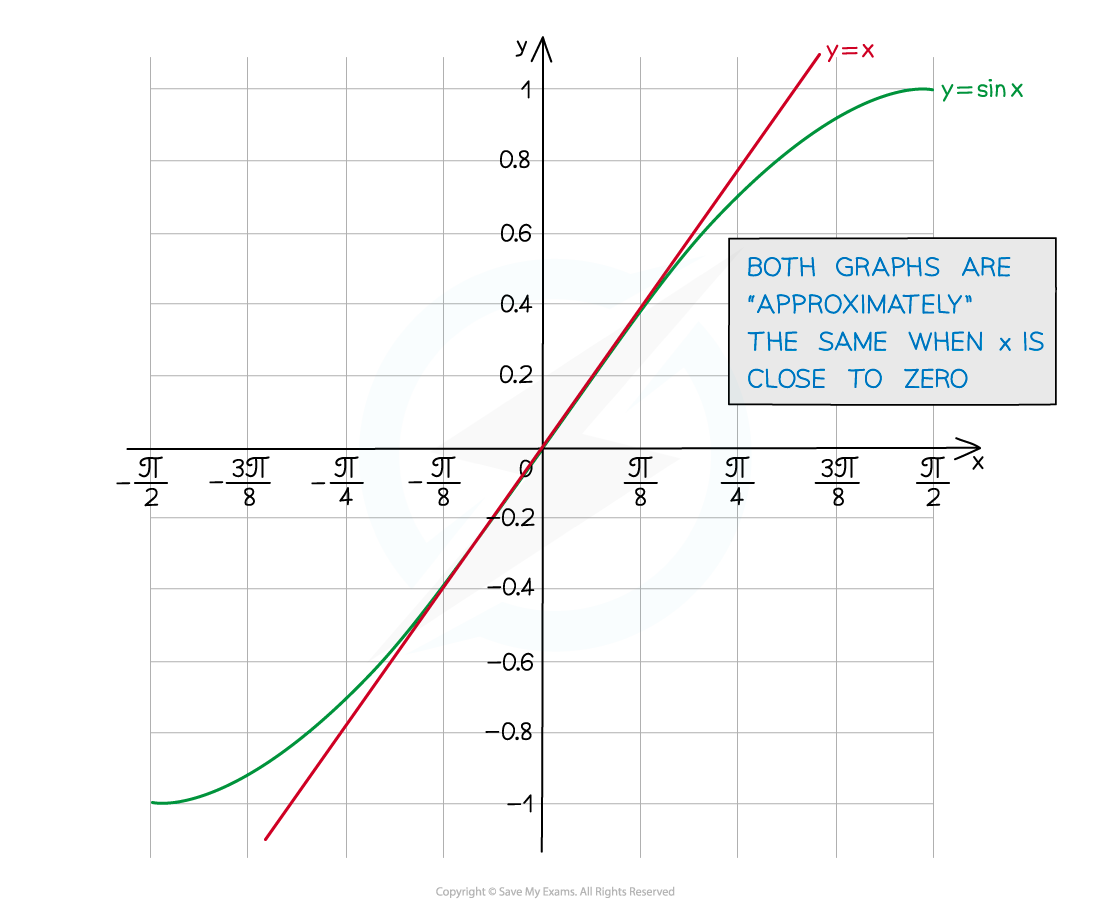
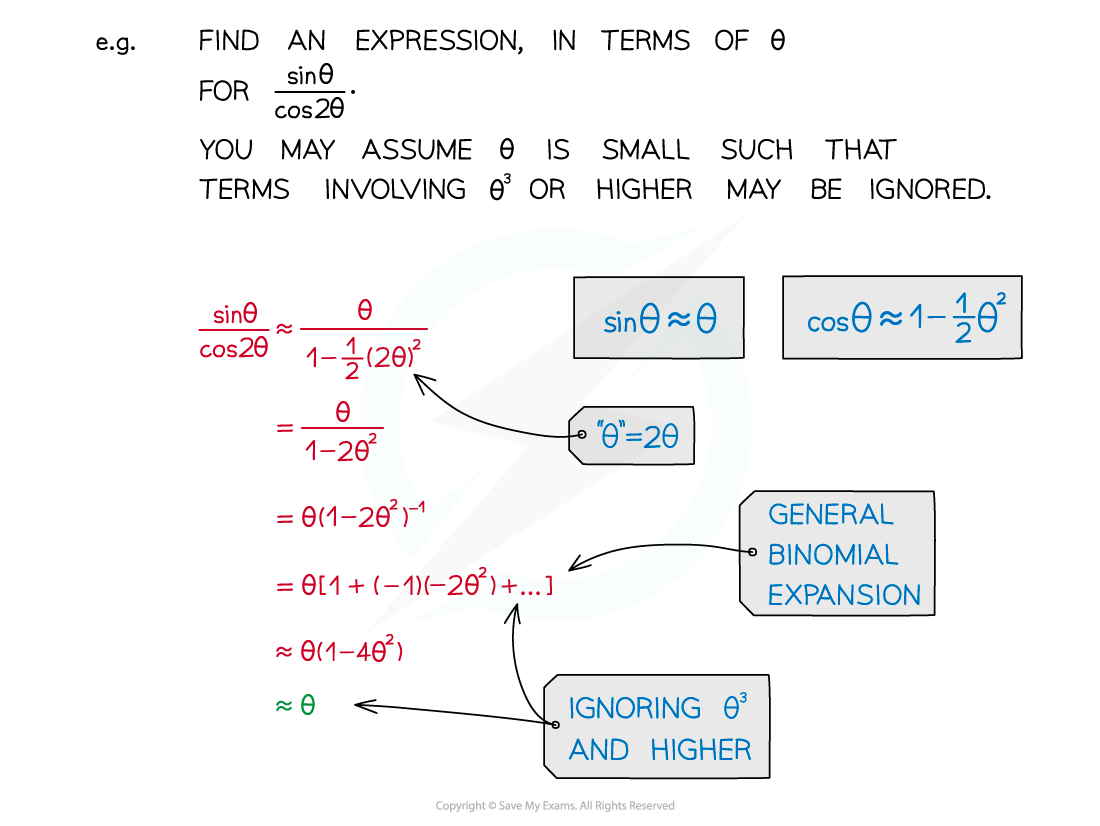
What's the small-angle approximation of sin θ?
sin θ ≈ θ
What's the small-angle approximation of cos θ?
cos θ ≈ 1 - θ2
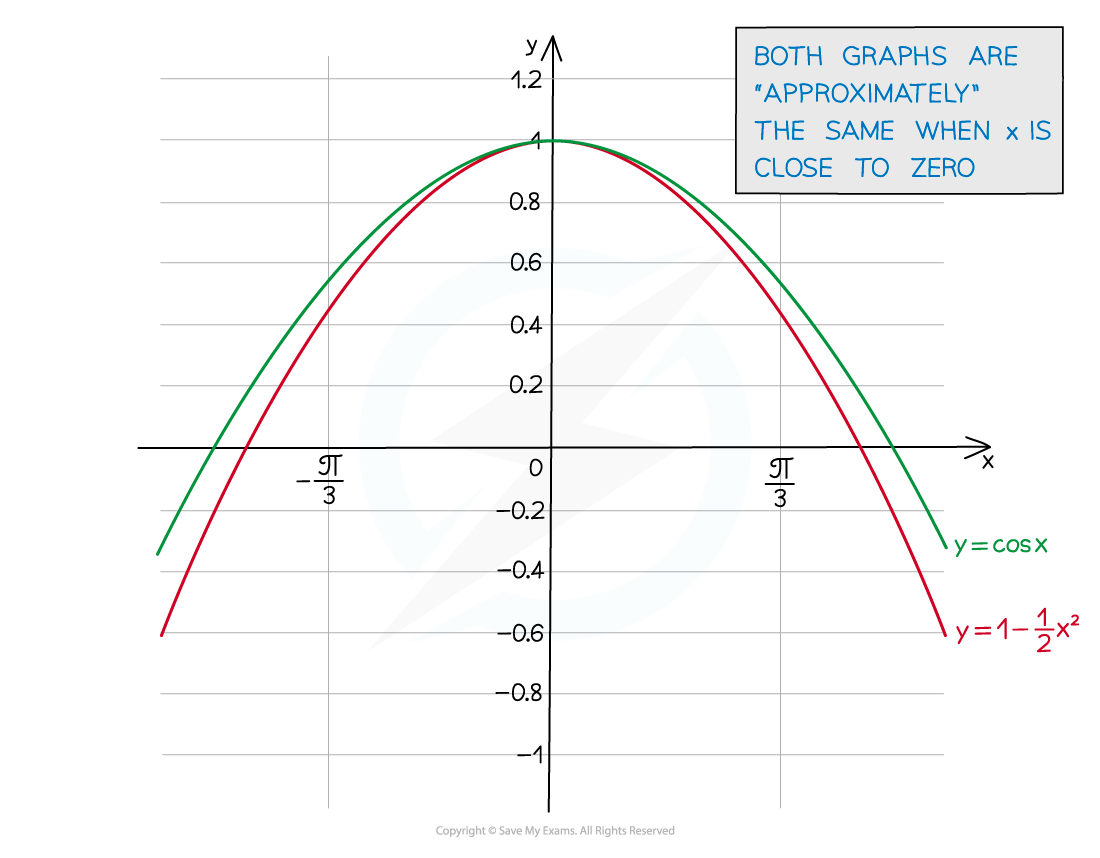
y = cos θ (near zero) is similar to a “negative quadratic” (parabola)
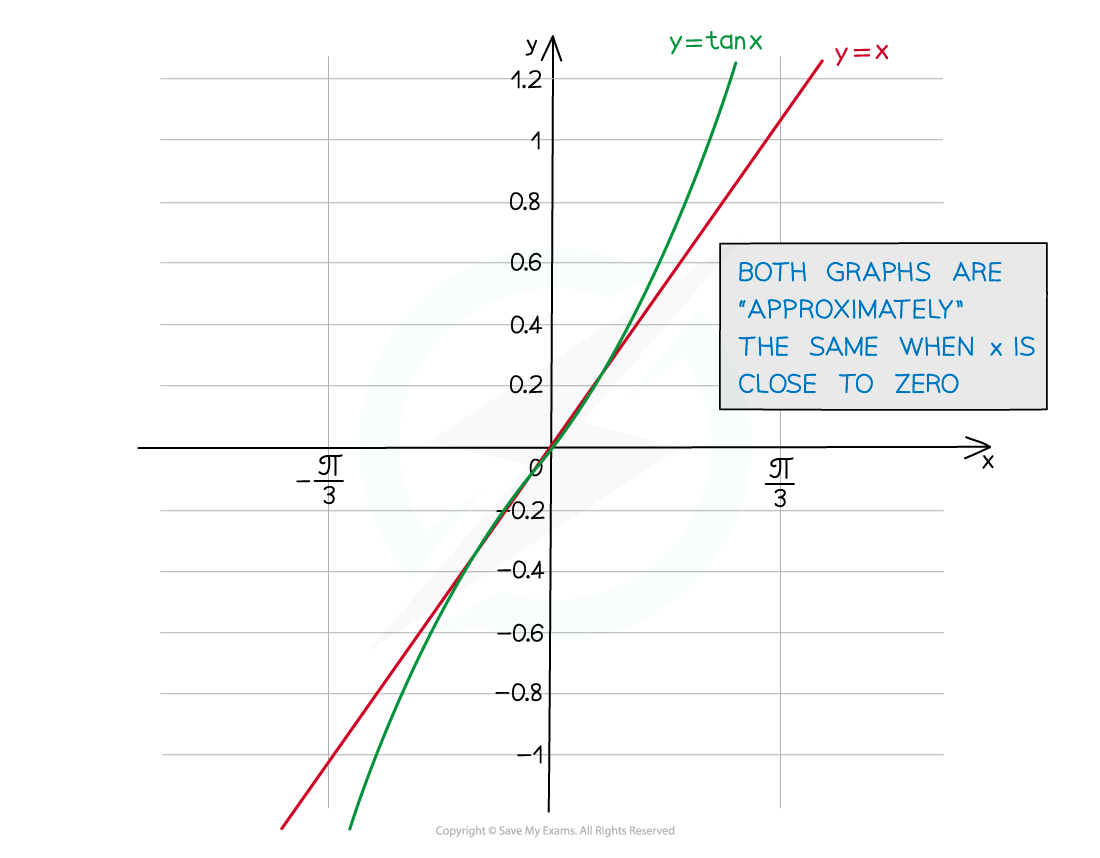
What's the small-angle approximation of tan θ?
tan θ ≈ θ
How do I use small angle approximations in solving problems?
Replace sin θ, cos θ or tan θ with the appropriate approximation
Given angles are often 2θ, 3θ, …
Replace “θ” in the approximation by 2θ, 3θ, …
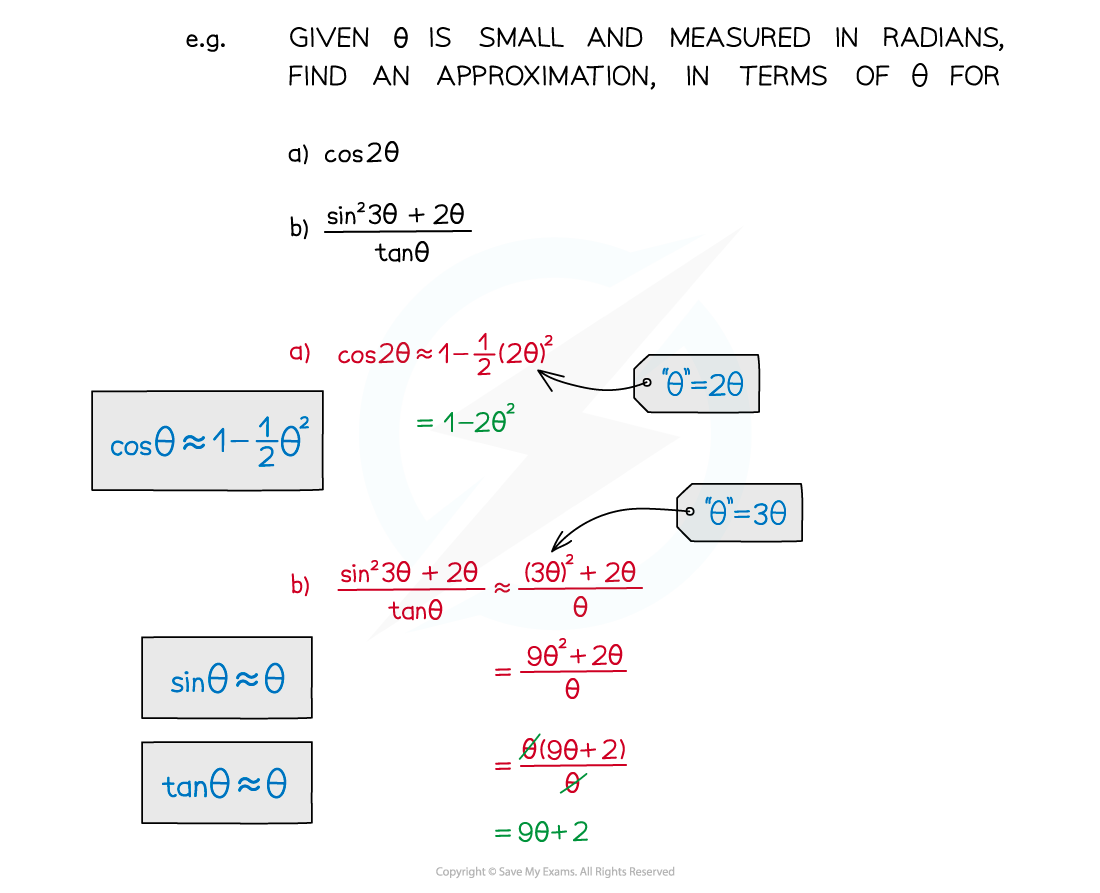
Binomial expansion (see GBE) may be involved in more awkward expressions
Examiner Tips and Tricks
Small angle approximations are given in the formula booklet.
They can be used in proofs – particularly differentiation from first principles (see First Principles Differentiation - Trigonometry).
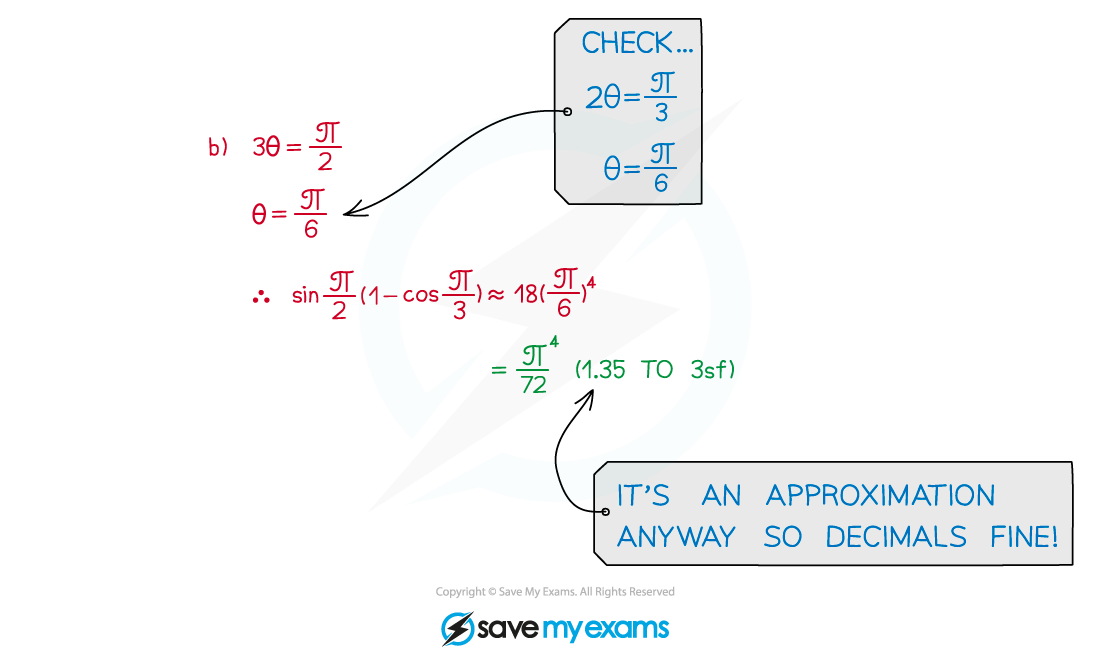
Worked Example


You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
