Solving Equations with Modulus Functions (OCR A Level Maths A) : Revision Note
Did this video help you?
Modulus Functions - Solving Equations
Modulus graphs and equations
Two non-parallel straight-line graphs would intersect once
If modulus involved there could be more than one intersection
Deducing where these intersections are is crucial to solving equations

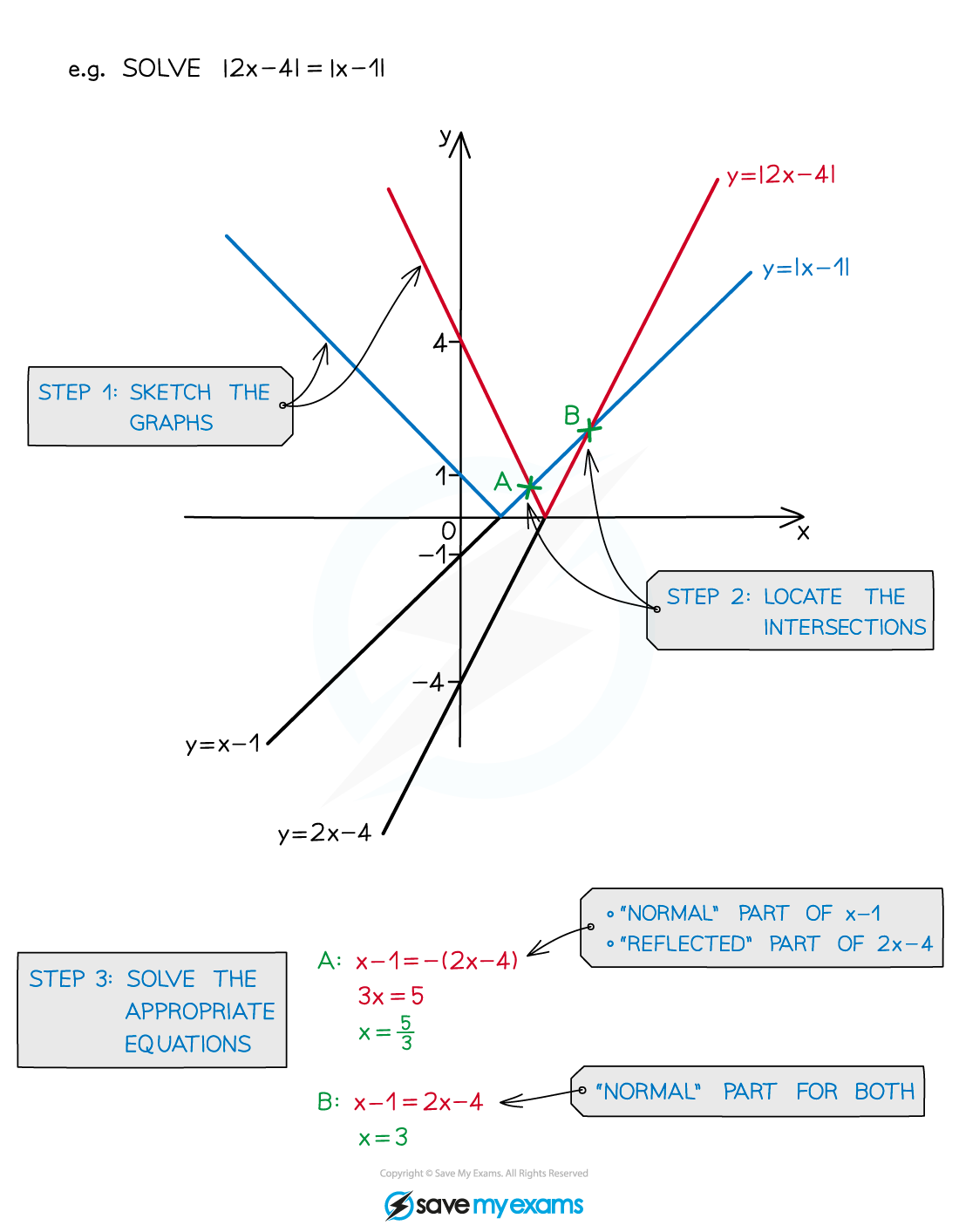
How do I solve modulus equations?
STEP 1 Sketch the graphs including any modulus (reflected) parts
(see Modulus Functions – Sketching Graphs)
STEP 2 Locate the graph intersections
STEP 3 Solve the appropriate equation(s) or inequality
For
the two possible equations are
and
Examiner Tips and Tricks
Sketching the graphs is important as solving algebraically can lead to invalid solutions.
For example, x = 1 is a solution to
but it is not a solution to
(substitute x = 1 into both sides and see why it does not work).
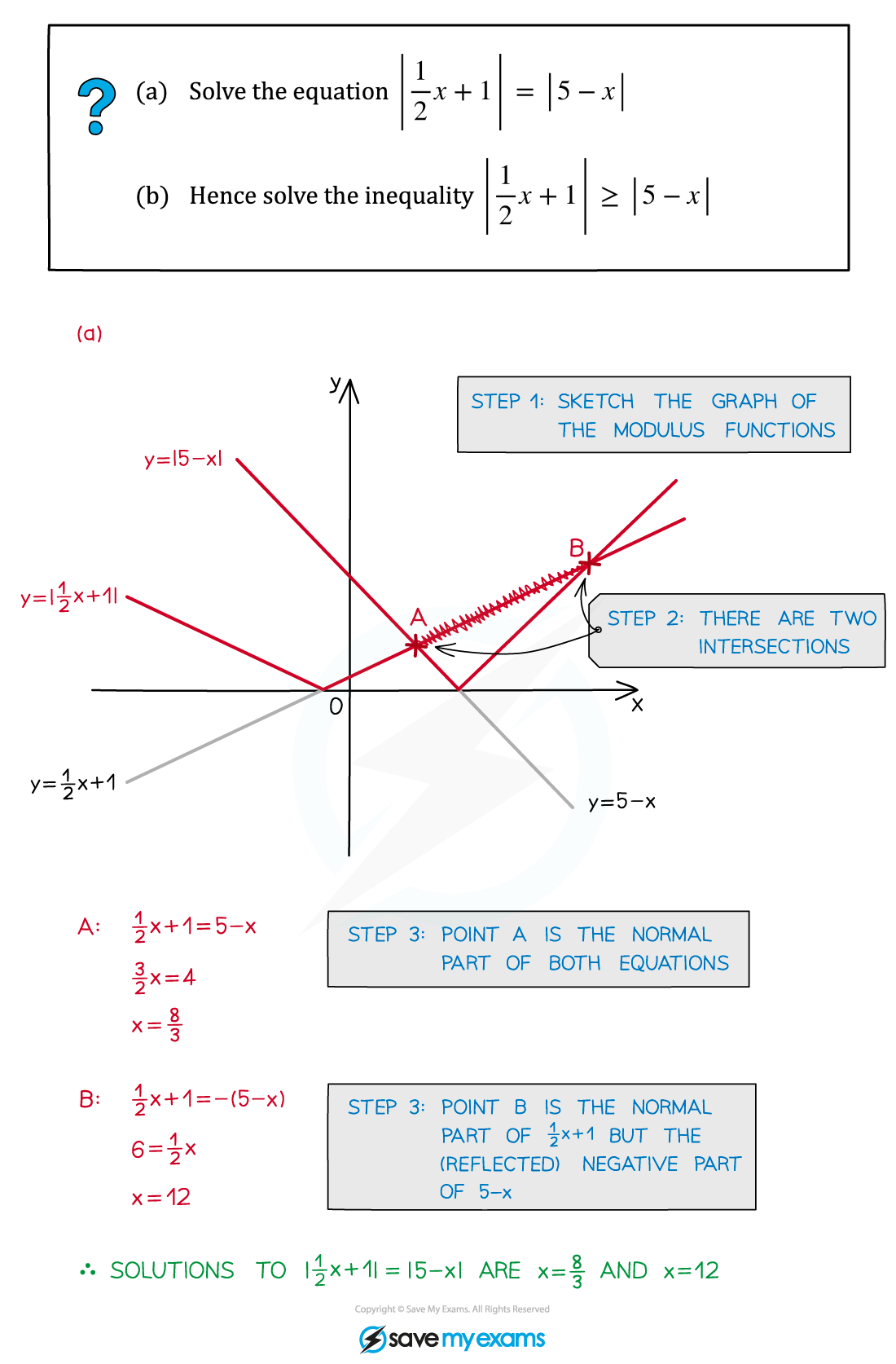
Worked Example


You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
