Revision NotesExam QuestionsPast PapersMock Exams
A LevelMathsEdexcelPureExam QuestionsIntegrationIntegration

Integration (Edexcel A Level Maths: Pure): Exam Questions

5 hours53 questions
Easy
Medium
Hard
Very Hard
1
Sme Calculator3 marks

Find

(i) integral 2 x space straight d x

(ii) integral 6 x squared space straight d x

(iii) integral 1 half x to the power of 1 half end exponent space straight d x

How did you do?

Did this page help you?

2
Sme Calculator4 marks

Find the value of

(i) integral subscript 1 superscript 2 4 x space straight d x

(ii) integral subscript 0 superscript 3 open parentheses 9 x squared plus 4 x close parentheses space straight d x

How did you do?

Did this page help you?

3
Sme Calculator2 marks

Find

space space integral open parentheses 3 x squared plus 5 x plus 3 close parentheses space straight d x

writing each term in simplest form.

How did you do?

Did this page help you?

4
Sme Calculator2 marks

Find

integral open parentheses 3 x to the power of 1 half end exponent plus 2 x to the power of negative 1 half space end exponent close parentheses straight d x

writing your answer in simplest form.

How did you do?

Did this page help you?

5
Sme Calculator2 marks

Find the value of

space integral subscript 1 superscript 5 left parenthesis 4 x plus 6 x squared right parenthesis space straight d x

How did you do?

Did this page help you?

6a
Sme Calculator2 marks

Write

fraction numerator 3 x cubed plus 4 x to the power of 6 over denominator x squared end fraction

in the form  3 x to the power of a plus 4 x to the power of b, where a and b are constants to be found.

How did you do?

6b
Sme Calculator2 marks

Hence find

integral open parentheses fraction numerator 3 x cubed plus 4 x to the power of 6 over denominator x squared end fraction close parentheses space straight d x

writing your answer in simplest form.

How did you do?

Did this page help you?

7a
Sme Calculator2 marks

Find

integral open parentheses 5 x to the power of 4 plus 6 x squared plus 2 x plus 3 close parentheses space straight d x

How did you do?

7b
Sme Calculator2 marks

Given that

  • space straight f apostrophe left parenthesis x right parenthesis equals 5 x to the power of 4 plus 6 x squared plus 2 x plus 3

  • the curve space y equals straight f left parenthesis x right parenthesis passes through the point open parentheses 1 comma space 10 close parentheses

find straight f left parenthesis x right parenthesis, giving your answer in simplest form.

How did you do?

Did this page help you?

8
Sme Calculator4 marks

A curve, C, is defined by the following:

  • fraction numerator straight d y over denominator straight d x end fraction equals 2 x cubed minus x

  • C passes through the point open parentheses 2 comma space minus 2 close parentheses

Show that the equation of C can be written in the form

space 2 y equals x to the power of 4 minus x squared plus k

where k is a constant to be found.

How did you do?

Did this page help you?

9a
Sme Calculator1 mark

The area bounded by the curve with equation space y equals 9 minus x squared, the x-axis and the vertical lines with equations x equals 1 and x equals 2 is shaded below.

Graph of y = 9 - x² with a shaded area between x = 1 and x = 2 and the x axis, bounded by dashed lines.

Write down a definite integral that represents this area.

How did you do?

9b
Sme Calculator2 marks

Use algebraic integration to find the exact area of the shaded region in part (a).

How did you do?

Did this page help you?

10
Sme Calculator4 marks

The diagram below shows the curve with equation y equals 7 x minus x squared minus 6 passing through the points open parentheses 1 comma space 0 close parentheses and open parentheses 6 comma space 0 close parentheses on the x-axis.

q9-8-1-integration-easy-a-level-maths-pure-screenshot

Use algebraic integration to find the exact area of the shaded region bounded by the curve and the x-axis.

How did you do?

Did this page help you?

11
Sme Calculator4 marks

The diagram below shows the curve with equation y equals x squared minus 8 x plus 12 passing through the points open parentheses 2 comma space 0 close parentheses and open parentheses 6 comma space 0 close parentheses on the x-axis.

q10-8-1-integration-easy-a-level-maths-pure-screenshot

Use algebraic integration to find the exact area of the shaded region.

How did you do?

Did this page help you?

12
Sme Calculator4 marks

A curve C has the equation y equals straight f open parentheses x close parentheses

Given that

  • straight f apostrophe open parentheses x close parentheses equals 3 minus 2 x plus 6 x squared

  • the curve passes through the point open parentheses 4 comma space 64 close parentheses

find the equation of the curve, giving your answer in simplest form.

How did you do?

Did this page help you?

13a
Sme Calculator1 mark

Simplify 

space x minus open parentheses x squared minus 8 x plus 18 close parentheses

How did you do?

13b
Sme Calculator4 marks

The diagram below shows the curve with equation y equals x squared minus 8 x plus 18 intersecting the straight line y equals x at the points open parentheses 3 comma space 3 close parentheses and open parentheses 6 comma space 6 close parentheses.

q11-8-1-integration-easy-a-level-maths-pure-screenshot

Use algebraic integration to find the exact area of the shaded region.

How did you do?

Did this page help you?

14
Sme Calculator4 marks

The finite region R, shown in the figure below, is bounded by the curve with equation y equals x squared minus 4 x plus 3 and the x-axis.

Use algebraic integration to find the exact area of R.

q11-8-1-integration-medium-a-level-maths-pure-screenshot

How did you do?

Did this page help you?

15
Sme Calculator4 marks

The figure below shows the finite shaded region, R, bounded by the curve y equals 2 x plus 3 x squared minus 2 x cubed and the x-axis.

q5-8-1-integration-hard-a-level-maths-pure-screenshot

Two x-intercepts of y equals 2 x plus 3 x squared minus 2 x cubed are shown, 0 and 2.

Use algebraic integration to find the exact area of R.

How did you do?

Did this page help you?

16
Sme Calculator3 marks

Find

integral open parentheses 3 minus 2 x close parentheses squared space straight d x

writing each term in simplest form.

How did you do?

Did this page help you?

14 marks

Find

integral open parentheses 8 x cubed minus fraction numerator 3 over denominator 2 square root of x end fraction plus 5 close parentheses space straight d x

giving your answer in simplest form.

How did you do?

Did this page help you?

24 marks

Find

integral fraction numerator x to the power of 1 half end exponent open parentheses 2 x minus 5 close parentheses over denominator 3 end fraction straight d x

writing each term in simplest form.

How did you do?

Did this page help you?

34 marks

Find

integral fraction numerator 3 x to the power of 4 minus 4 over denominator 2 x cubed end fraction straight d x

writing your answer in simplest form.

How did you do?

Did this page help you?

4a
Sme Calculator2 marks

The curve C has equation y equals straight f open parentheses x close parentheses

The curve

  • passes through the point P open parentheses 3 comma space minus 10 close parentheses

  • has a turning point at P

Given that

fraction numerator straight d y over denominator straight d x end fraction equals 2 x cubed minus 9 x squared plus 5 x plus k

where k is a constant,

show that k equals 12.

How did you do?

4b
Sme Calculator3 marks

Hence find the coordinates of the point where C crosses the y-axis.

How did you do?

Did this page help you?

5
Sme Calculator4 marks

Find the value of the constant k, 0 less than k less than 9, such that

integral subscript k superscript 9 fraction numerator 6 over denominator square root of x end fraction straight d x equals 20

How did you do?

Did this page help you?

6
Sme Calculator4 marks

Find the value of the positive constant k such that

integral subscript k superscript 5 space space left parenthesis 2 x minus 1 right parenthesis space straight d x equals 20

How did you do?

Did this page help you?

7a
Sme Calculator3 marks

Find

integral open parentheses x squared plus 5 minus 3 over x squared close parentheses space straight d x

giving your answer in simplest form.

How did you do?

7b
Sme Calculator2 marks

Write down

integral 3 e to the power of 3 x end exponent space d x

How did you do?

Did this page help you?

8
Sme Calculator6 marks

The figure below shows a sketch of the line y equals 2 and the curve with equation y equals x squared minus 4 x plus 5.

q9-8-1-integration-medium-a-level-maths-pure-screenshot

Use algebraic integration to find the exact area of R.

How did you do?

Did this page help you?

9
Sme Calculator6 marks

The curve with equation y equals x squared and the straight line with equation y equals 6 minus x are shown in the figure below.

The finite region bounded by the curve, the line and the x-axis is shaded.

GztGkQjs_q10-8-1-integration-easy-a-level-maths-pure-screenshot

Use algebraic integration to find the exact area of the shaded region.

How did you do?

Did this page help you?

10
Sme Calculator5 marks

Find the exact value of

integral subscript 4 superscript 9 fraction numerator x squared space plus space 1 over denominator square root of x end fraction space straight d x

How did you do?

Did this page help you?

11
Sme Calculator5 marks

The finite region R, shown in the figure below, is bounded by the curve with equationspace y equals 4 minus open parentheses x minus 2 close parentheses squared and the x-axis.

q5-8-1-integration-easy-a-level-maths-pure-screenshot

The x-intercepts of the curve space y equals 4 minus open parentheses x minus 2 close parentheses squared are 0 and 4.

Use algebraic integration to find the exact area of R.

How did you do?

Did this page help you?

12
Sme Calculator3 marks

Find

integral open parentheses 2 square root of x plus 5 x to the power of 1 third end exponent close parentheses space straight d x

giving your answer in simplest form.

How did you do?

Did this page help you?

13
Sme Calculator4 marks

A curve has the equation y equals straight f open parentheses x close parentheses

Given that

  • straight f apostrophe open parentheses x close parentheses equals 3 minus 2 x plus 4 over x squared

  • the curve passes through the point open parentheses negative 2 comma space 3 close parentheses

find the equation of the curve, giving your answer in simplest form.

How did you do?

Did this page help you?

14
Sme Calculator3 marks

Find the integer value of b such that

integral subscript negative 3 end subscript superscript 4 open parentheses 2 k x plus 3 k x squared close parentheses space straight d x equals b k

where k is a constant.

How did you do?

Did this page help you?

15a
Sme Calculator3 marks

A curve has the equation y equals straight f open parentheses x close parentheses

Given that

  • fraction numerator straight d squared y over denominator straight d x squared end fraction space equals 30 x

  • fraction numerator d y over denominator d x end fraction equals 17 when x equals 1

find an expression for fraction numerator d y over denominator d x end fraction

How did you do?

15b
Sme Calculator3 marks

Given that

  • y equals 40 when x equals 2

find the equation of the curve, y equals straight f open parentheses x close parentheses, giving your answer in simplest form.

How did you do?

Did this page help you?

16
Sme Calculator6 marks

The figure below shows a sketch of the curve with equation y equals x left parenthesis x minus 1 right parenthesis left parenthesis x plus 2 right parenthesis.

q7-8-1-integration-hard-a-level-maths-pure-screenshot

Use algebraic integration to find the total area of the shaded regions.

How did you do?

Did this page help you?

17
Sme Calculator4 marks

The curve C has the equation y equals straight f open parentheses x close parentheses

Given that

  • straight f apostrophe open parentheses x close parentheses equals fraction numerator 2 over denominator square root of x end fraction minus x minus 3

  • C passes through the point open parentheses 4 comma negative 8 close parentheses

find the equation of C, giving your answer in simplest form.

How did you do?

Did this page help you?

18a
Sme Calculator4 marks

The curve with equation y equals 4 x minus x cubed is shown in the figure below.

q6-8-1-integration-vh-a-level-maths-pure-screenshot

The region bounded by the curve and the x-axis, where x less or equal than 0 and y less or equal than 0, is shaded.

Using algebraic integration, find the exact area of R.

How did you do?

18b
Sme Calculator1 mark

Write down the value of 

integral subscript negative 2 end subscript superscript 2 space open parentheses 4 x minus x cubed space close parentheses straight d x

How did you do?

Did this page help you?

15 marks

In this question you must show all stages of your working.

Solutions relying on calculator technology are not acceptable.

Graph showing the shaded region R above the curve y=4(x^2)+3, below the horizontal line y=23, and to the right of the y-axis, with labelled x and y axes and origin point O.
Figure 2

The finite region R, shown shaded in Figure 2, is bounded by the curve with equation y equals 4 x squared plus 3, the y-axis and the line with equation y equals 23

Show that the exact area of R is k square root of 5 where k is a rational constant to be found.

How did you do?

Did this page help you?

26 marks

In this question you must show all stages of your working.

Solutions relying on calculator technology are not acceptable.

Graph of a curve on xy-axes for positive values of x, with a shaded region labelled R below the x-axis enclosed by the curve and the x-axis.
Figure 3

Figure 3 shows a sketch of part of a curve with equation

y equals fraction numerator open parentheses x minus 2 close parentheses open parentheses x minus 4 close parentheses over denominator 4 square root of x end fraction space space space space space space space space space space space space space x greater than 0

The region R, shown shaded in Figure 3, is bounded by the curve and the x-axis.

Find the exact area of R, writing your answer in the form a square root of 2 plus b , where a and b are constants to be found.

How did you do?

Did this page help you?

3a5 marks
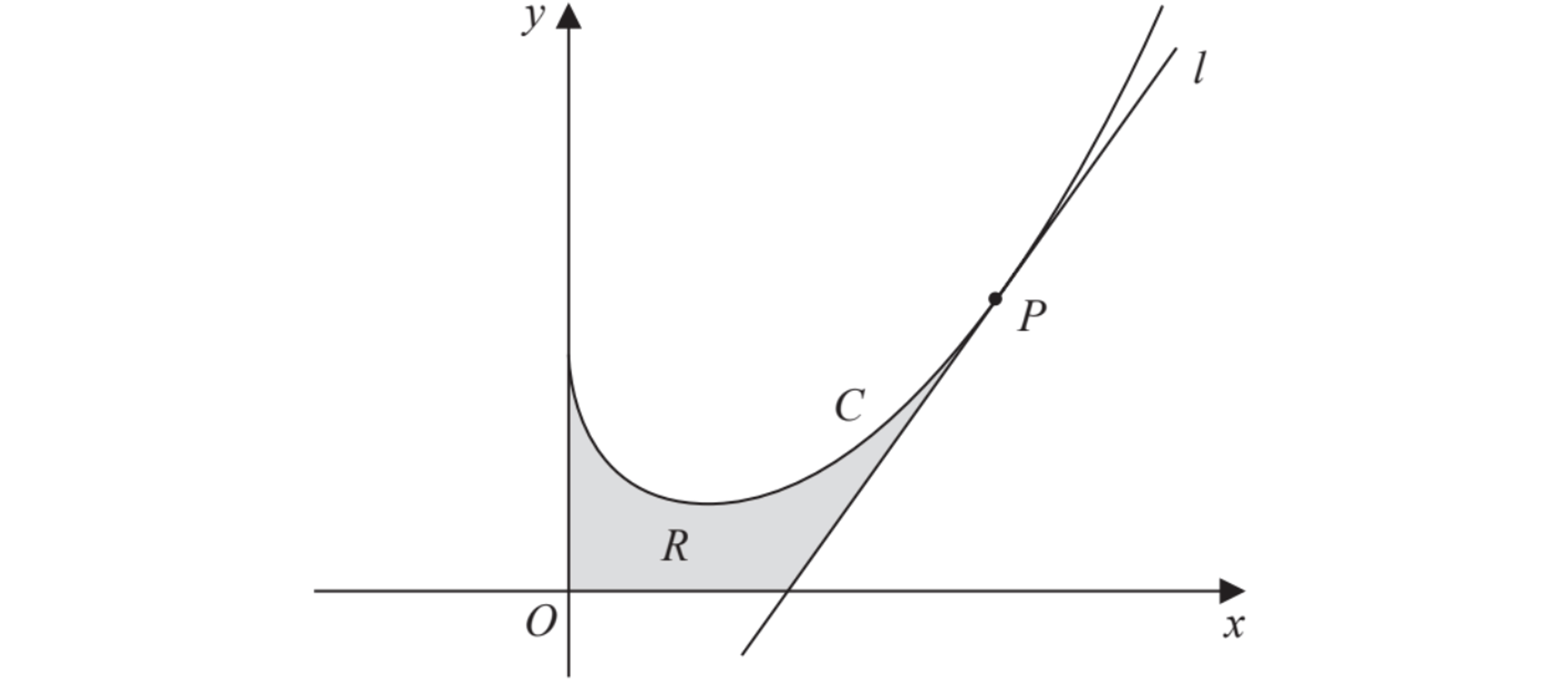
Graph showing a curve C and a tangent line l, that touches the curve at point P. The region bounded by C, l and the coordinate axes is shaded and labelled R.
Figure 2

In this question your must show all stages of your working.

Solutions relying on calculator technology are not acceptable.

Figure 2 shows a sketch of part of the curve C with equation

table row cell y equals 1 third x squared minus 2 square root of x plus 3 end cell blank cell x greater or equal than 0 end cell end table

The point P lies on C and has x coordinate 4

The line l is tangent to C at P.

Show that l has equation

13 x minus 6 y minus 26 equals 0

How did you do?

3b
Sme Calculator5 marks

The region R, shown shaded in Figure 2 is bounded by the y-axis, the curve C, the line l and the x-axis.

Find the exact area of R.

How did you do?

Did this page help you?

4
Sme Calculator5 marks

Find the value of

integral subscript 2 superscript 4 fraction numerator x cubed plus cube root of x over denominator 2 square root of x end fraction space d x

giving your answer correct to 3 significant figures.

How did you do?

Did this page help you?

5
Sme Calculator5 marks

Find

integral open parentheses 2 minus x close parentheses cubed space straight d x

writing each term in simplest form.

How did you do?

Did this page help you?

6
Sme Calculator5 marks

Find the value of the constant p, where p greater than 0, such that

integral subscript 1 superscript p left parenthesis 1 plus 1 over x squared right parenthesis space straight d x equals 15 over 4

How did you do?

Did this page help you?

7
Sme Calculator5 marks

The function straight f open parentheses x close parentheses has the following properties

  • straight f apostrophe apostrophe open parentheses x close parentheses equals 6 left parenthesis x minus 2 right parenthesis

  • straight f apostrophe open parentheses 2 close parentheses equals 8

  • straight f open parentheses 3 close parentheses equals 20

Find straight f open parentheses x close parentheses, giving your answer in simplest form.

How did you do?

Did this page help you?

8
Sme Calculator6 marks

The figure below shows the straight line with equation 5 y equals 14 minus 3 x and the curve with equation 5 y equals 20 minus 2 x minus x squared.

The shaded region R is bounded by the curve and the straight line.

q9-8-1-integration-hard-a-level-maths-pure-screenshot

Use algebraic integration to find the exact area of R.

How did you do?

Did this page help you?

9
Sme Calculator7 marks

The figure below shows the straight line y equals x plus 2 and the curve with equation y equals 10 x minus x squared minus 16.

q10-8-1-integration-hard-a-level-maths-pure-screenshot

Use algebraic integration to find the exact area of the shaded region.

How did you do?

Did this page help you?

10
Sme Calculator8 marks

The curve with equation y equals x cubed minus 2 x squared minus x plus 2 is shown in the figure below.

q8-8-1-integration-vh-a-level-maths-pure-screenshot

Use algebraic integration to find the total area of the shaded regions.

How did you do?

Did this page help you?

11a3 marks

A curve C has equation y equals straight f open parentheses x close parentheses where

straight f left parenthesis x right parenthesis equals – 3 x squared plus 12 x plus 8

Write straight f open parentheses x close parentheses in the form

a open parentheses x plus b close parentheses squared plus c

where a, b and c are constants to be found.

How did you do?

11b2 marks

The curve C has a maximum turning point at M.

Find the coordinates of M.

How did you do?

11c
Sme Calculator5 marks
Graph with an 'n-shaped' parabola labelled C, with a vertex maximum point in the first quadrant labelled M. A horizontal line l is tangent to the parabola at point M. The region in the first quadrant enclosed by the parabola, line l, and the positive y-axis, is shaded and labelled R. The x- and y-axes are shown and labelled.
Figure 3

Figure 3 shows a sketch of the curve C.

The line l passes through M and is parallel to the x-axis.

The region R, shown shaded in Figure 3, is bounded by C, l and the y-axis.

Using algebraic integration, find the area of R.

How did you do?

Did this page help you?

1
Sme Calculator6 marks

A curve has equation y equals straight f open parentheses x close parentheses, space x greater or equal than 0

Given that

  • straight f to the power of apostrophe open parentheses x close parentheses equals 4 x plus a square root of x plus b, where a and b are constants

  • the curve has a stationary point at open parentheses 4 comma space 3 close parentheses

  • the curve meets the y-axis at negative 5

find straight f open parentheses x close parentheses, giving your answer in simplest form.

How did you do?

Did this page help you?

2a4 marks
Graph with a positive cubic curve. The intersects the x-axis at 3 points, once on the negative x-axis, at (0, 0) and once on the positive x-axis. The region below the curve and above the x-axis between the first two points of intersection is shaded and labelled R1. The region above the curve and below the x-axis between the second point of intersection and the point b on the positive x-axis is shaded and labelled R2.
Figure 2

Figure 2 shows a sketch of part of the curve with equation y equals x open parentheses x plus 2 close parentheses open parentheses x minus 4 close parentheses.

The region R subscript 1 shown shaded in Figure 2 is bounded by the curve and the negative x-axis.

Show that the exact area of R subscript 1 is 20 over 3

How did you do?

2b4 marks

The region R subscript 2 also shown shaded in Figure 2 is bounded by the curve, the positive x-axis and the line with equation x equals b, where b is a positive constant and 0 less than b less than 4

Given that the area of R subscript 1 is equal to the area of R subscript 2 verify that b satisfies the equation

open parentheses b plus 2 close parentheses squared open parentheses 3 b squared minus 20 b plus 20 close parentheses equals 0

How did you do?

2c2 marks

The roots of the equation 3 b squared minus 20 b plus 20 equals 0 are 1.225 and 5.442 to 3 decimal places.

The value of b is therefore 1.225 to 3 decimal places.

Explain, with the aid of a diagram, the significance of the root 5.442

How did you do?

Did this page help you?

3a4 marks

In this question you should show all stages of your working.

Solutions relying entirely on calculator technology are not acceptable.

Graph with curve C and line l intersecting at point P(5, -13). Shaded region R is beneath the curve and above the line, with axes labelled x and y.

Figure 2 shows a sketch of part of the curve C with equation

y equals x cubed minus 10 x squared plus 27 x minus 23

The point P open parentheses 5 comma space minus 13 close parentheses lies on C

The line l is tangent to C at P

Use differentiation to find the equation of l, giving your answer in the form y equals m x plus c where m and c are integers to be found.

How did you do?

3b
Sme Calculator1 mark

Hence verify that l meets C again on the y-axis.

How did you do?

3c4 marks

The finite region R, shown shaded in Figure 2, is bounded by the curve C and the line l.

Use algebraic integration to find the exact area of R.

How did you do?

Did this page help you?

4
Sme Calculator6 marks

Given that

integral open parentheses 2 open parentheses 3 minus 1 half x close parentheses close parentheses to the power of p space straight d x equals negative 1 fourth x to the power of 4 plus...

where p is a positive integer and negative 1 fourth x to the power of 4 is the term with the highest power of x, find fully

integral open parentheses 2 open parentheses 3 minus 1 half x close parentheses close parentheses to the power of p space straight d x

writing each term in simplest form.

How did you do?

Did this page help you?

5
Sme Calculator5 marks

Find the value of the constant q such that

integral subscript q superscript 4 q end superscript 5 x square root of x space straight d x equals 15 space 066

How did you do?

Did this page help you?

6
Sme Calculator6 marks

A function, straight f left parenthesis x right parenthesis

  • has a factor of open parentheses 2 x minus 1 close parentheses

  • has a factor of open parentheses 3 x plus 2 close parentheses

  • has a second derivative of straight f apostrophe apostrophe open parentheses x close parentheses equals 2 open parentheses 18 x minus 5 close parentheses

Find straight f left parenthesis x right parenthesis

How did you do?

Did this page help you?

7
Sme Calculator8 marks

The straight line with equation 4 y equals 4 x plus 17 and the curve with equation y equals 3 x squared minus 8 x minus 16 are shown in the figure below.

The region bounded by the straight line, the curve and the x-axis is shaded.

q6-8-1-integration-vhard-a-level-maths-pure-screenshot

Use algebraic integration to find the exact area of the shaded region.

How did you do?

Did this page help you?

8
Sme Calculator9 marks

The figure below shows a sketch of the line y equals 16 minus 2 x and the curve y equals x cubed minus 15 x squared plus 66 x minus 80.

Use algebraic integration to find the exact total area of the shaded regions.

q7-8-1-integration-vhard-a-level-maths-pure-screenshot

How did you do?

Did this page help you?