Separation of Variables (Edexcel A Level Maths) : Revision Note
Did this video help you?
Separation of Variables
What does separation of variables mean?

Many differential equations used in modelling either …
… have two variables involved (ie x and y), or,
... involve a function of the dependent variable (ie y) only
This is particularly true where proportionality is involved
eg population change is dependent on both time and the size of the population

This type of question is covered in more detail in Modelling with Differential Equations
How do I know if I need to separate the variable in a question?
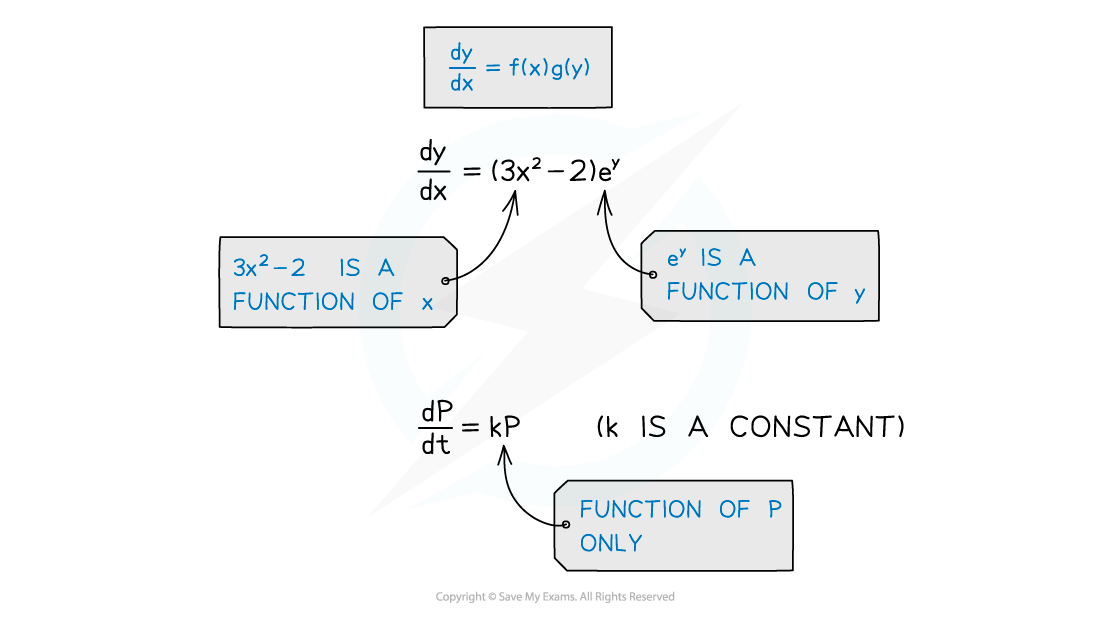
There is a product of functions in different variables
ie dy/dx = f(x) × g(y)
It will not be possible to integrate directly from an equation in the form dy/dx= g(y)
How do I solve a separating variables question?
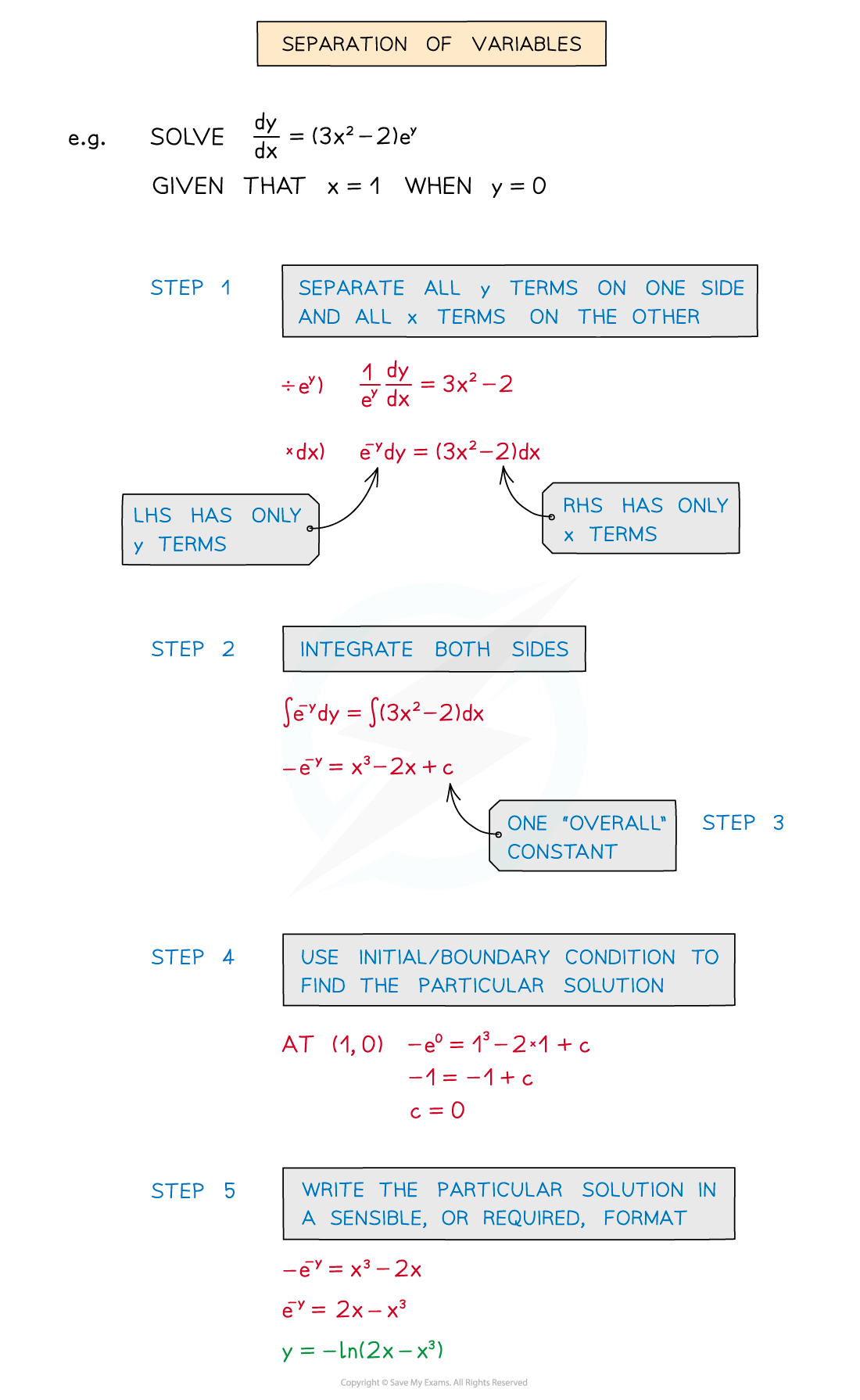
STEP 1: Separate all y terms on one side and all x terms on the other side
STEP 2: Integrate both sides
STEP 3: Include one “overall” constant of integration
STEP 4: Use the initial or boundary condition to find the particular solution
STEP 5: Write the particular solution in sensible, or required, format
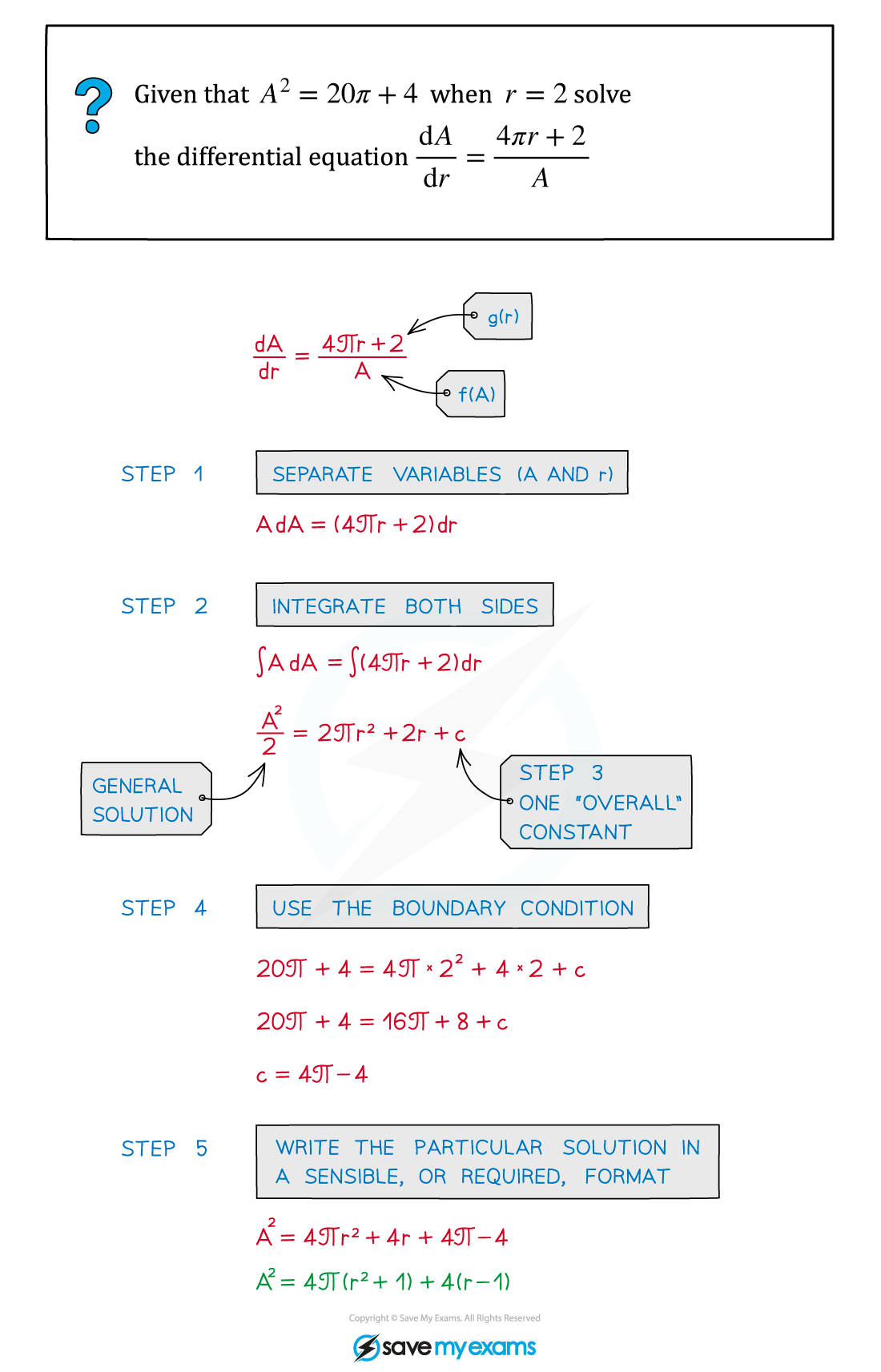
Worked Example

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?
