Basics of Parametric Equations (Edexcel A Level Maths): Revision Note
Exam code: 9MA0
Did this video help you?
Basics of parametric equations
What are parametric equations?
Graphs are usually described by a Cartesian equation
The equation involves x and y only
Equations like this can sometimes be rearranged into the form, y = f(x)
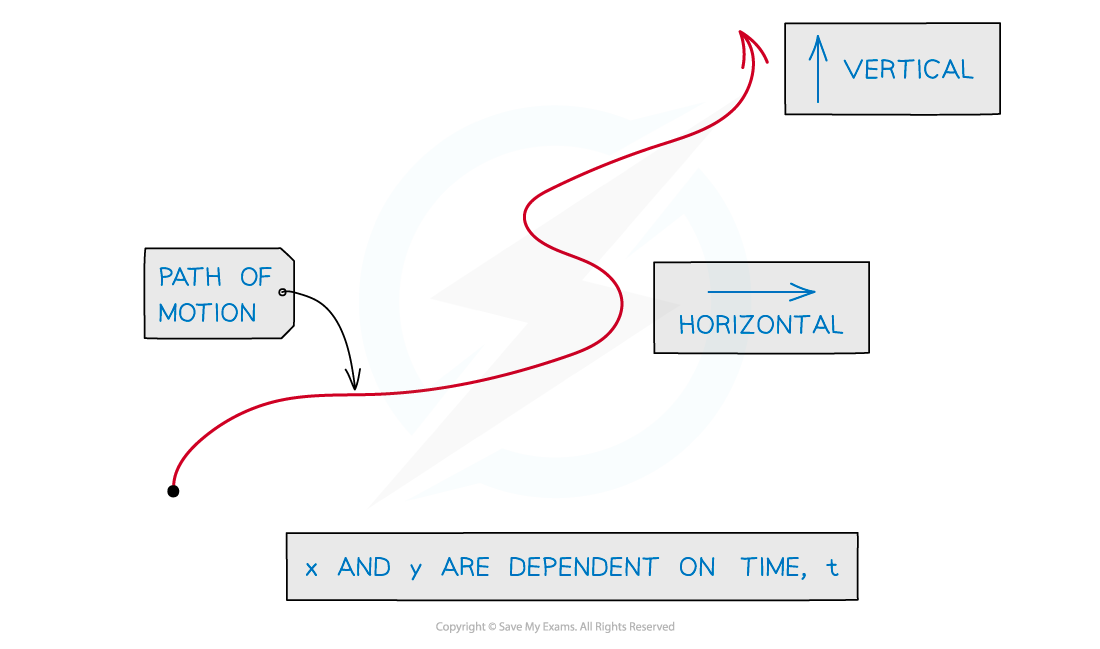
In parametric equations both x and y are dependent on a third variable
This is called a parameter
t and θ are often used as parameters
A common example …
x is the horizontal position of an object
y is the vertical position of an object
and the position of the object is dependent on time t
x is a function of t, y is a function of t
x = f(t)
y = g(t)
How do I plot parametric equations?
It is still possible to plot a graph of y against x from their parametric equations
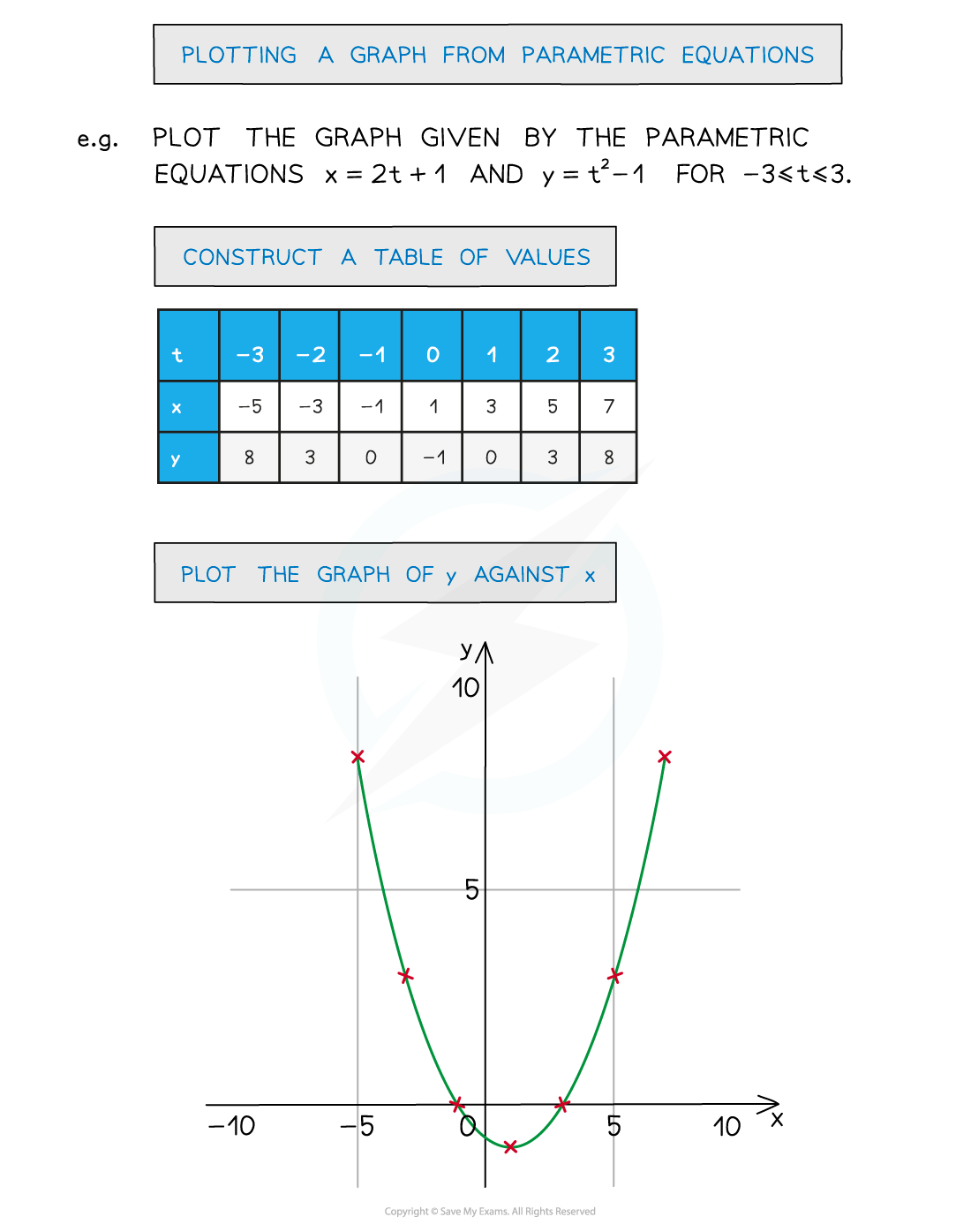
Also see Parametric Equations – Sketching Graphs
What are the parametric equations of a circle?
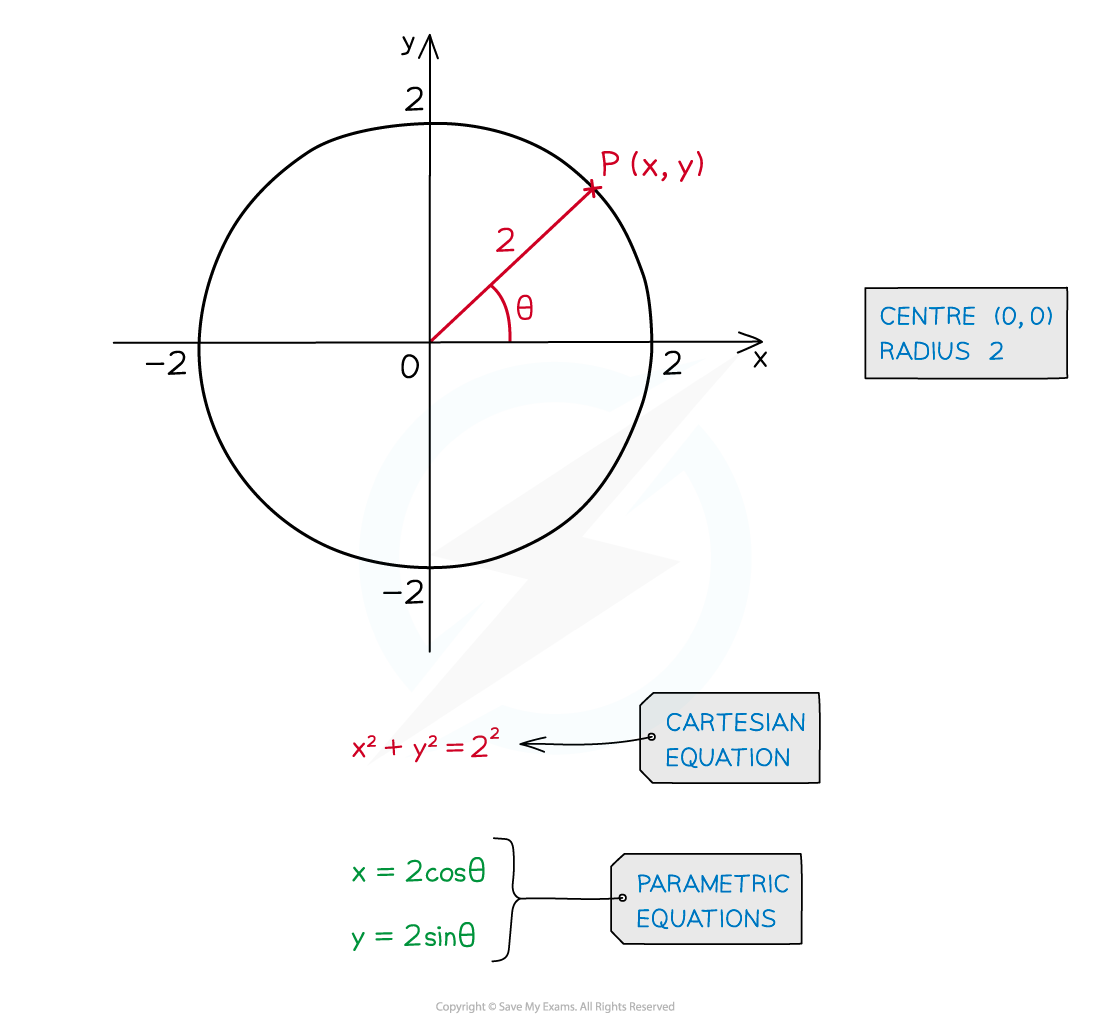
For a circle, centre (0, 0) and radius r
x = rcos θ
y = rsin θ
(Note that r is constant, this is not two parameters)
For a circle, centre (a, b) and radius r
x = rcos θ + a
y = rsin θ + b
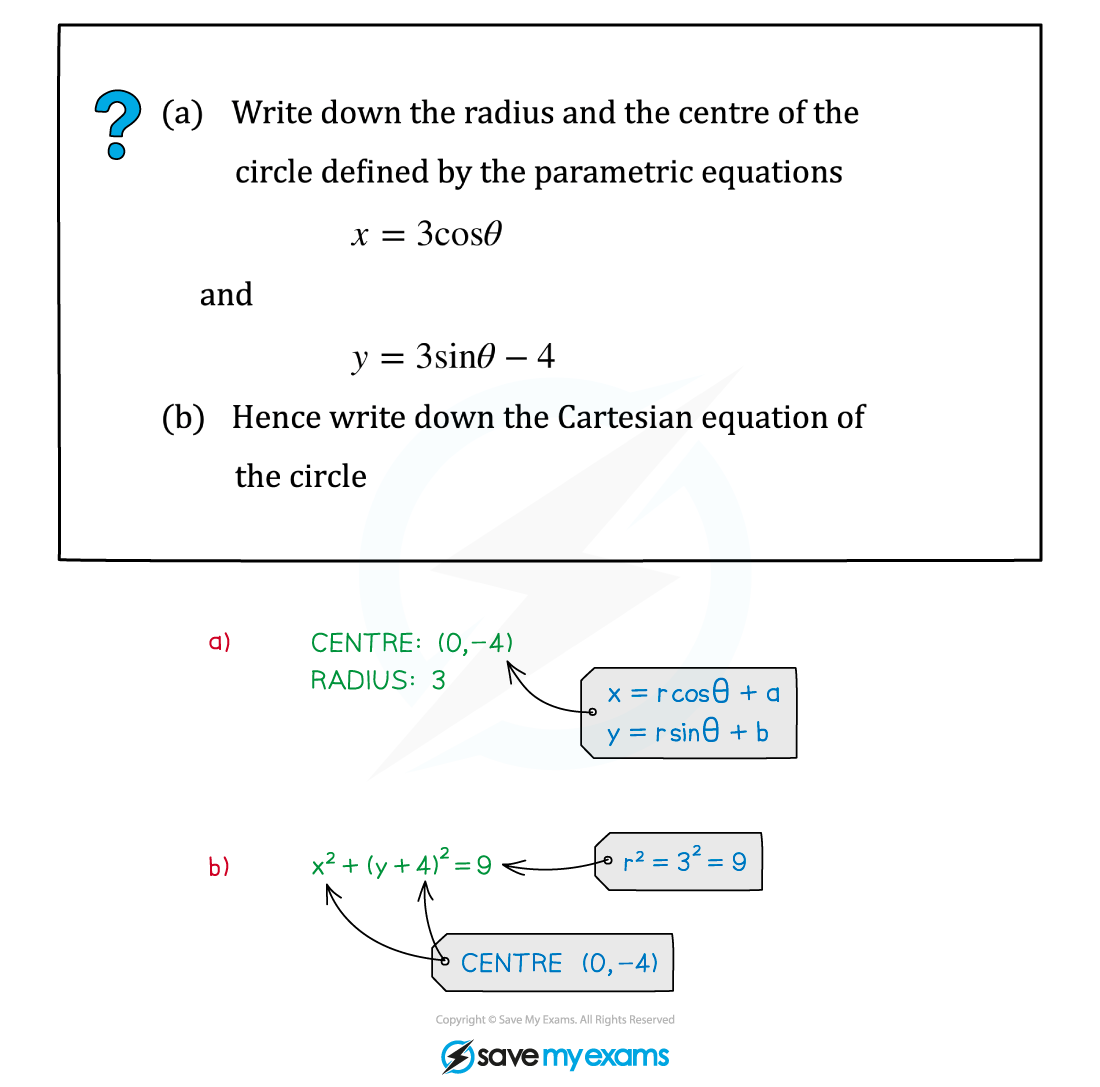
Worked Example

Unlock more, it's free!
Did this page help you?