Area Under a Curve (Edexcel A Level Maths) : Revision Note
Did this video help you?
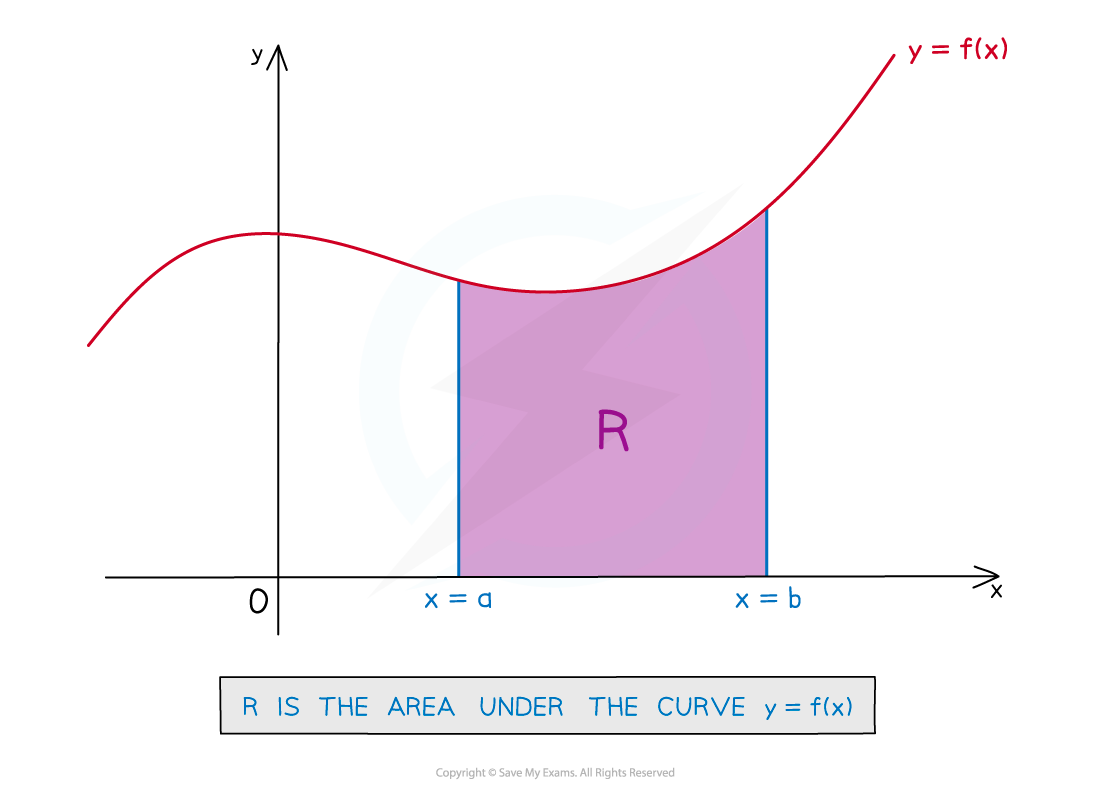
Area Under a Curve
What does area under a curve mean?
The phrase “area under a curve” refers to the area bounded by …
... the x-axis
… the graph of y = f(x)
… the vertical line x = a
… the vertical line x = b
How do I find the area under a curve?
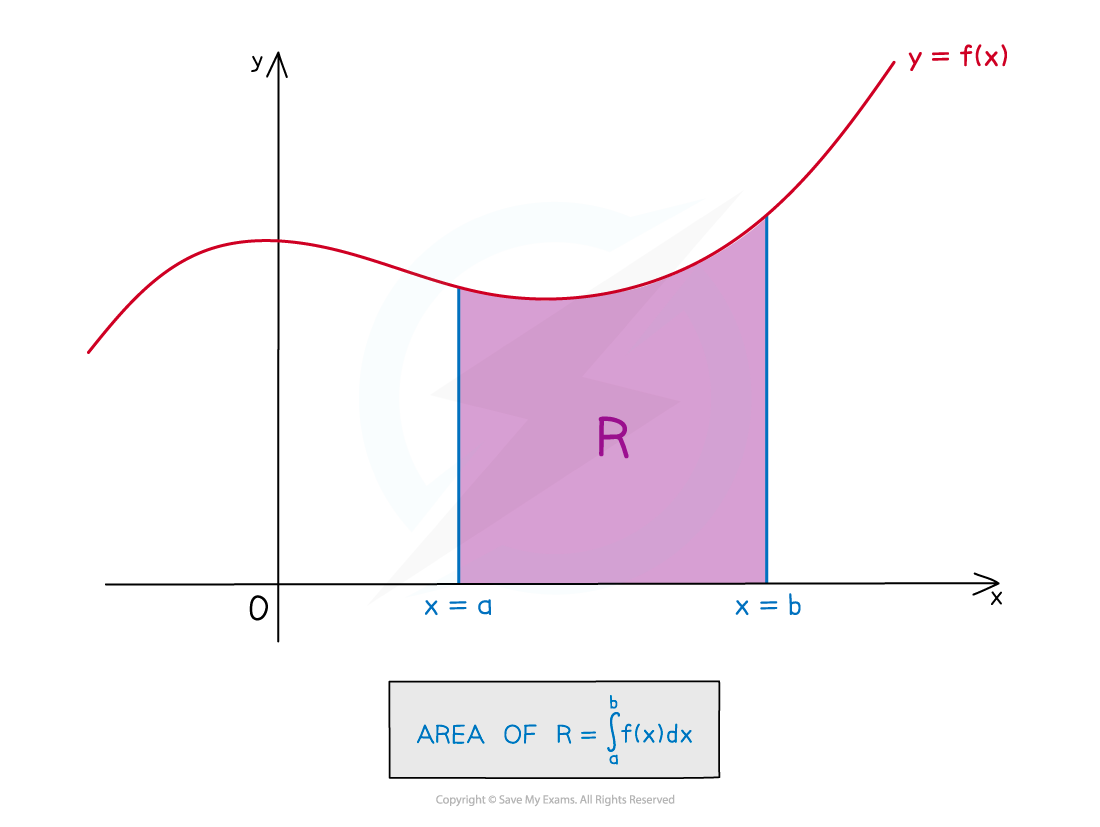
The value from definite integration is equal to the “area under a curve”
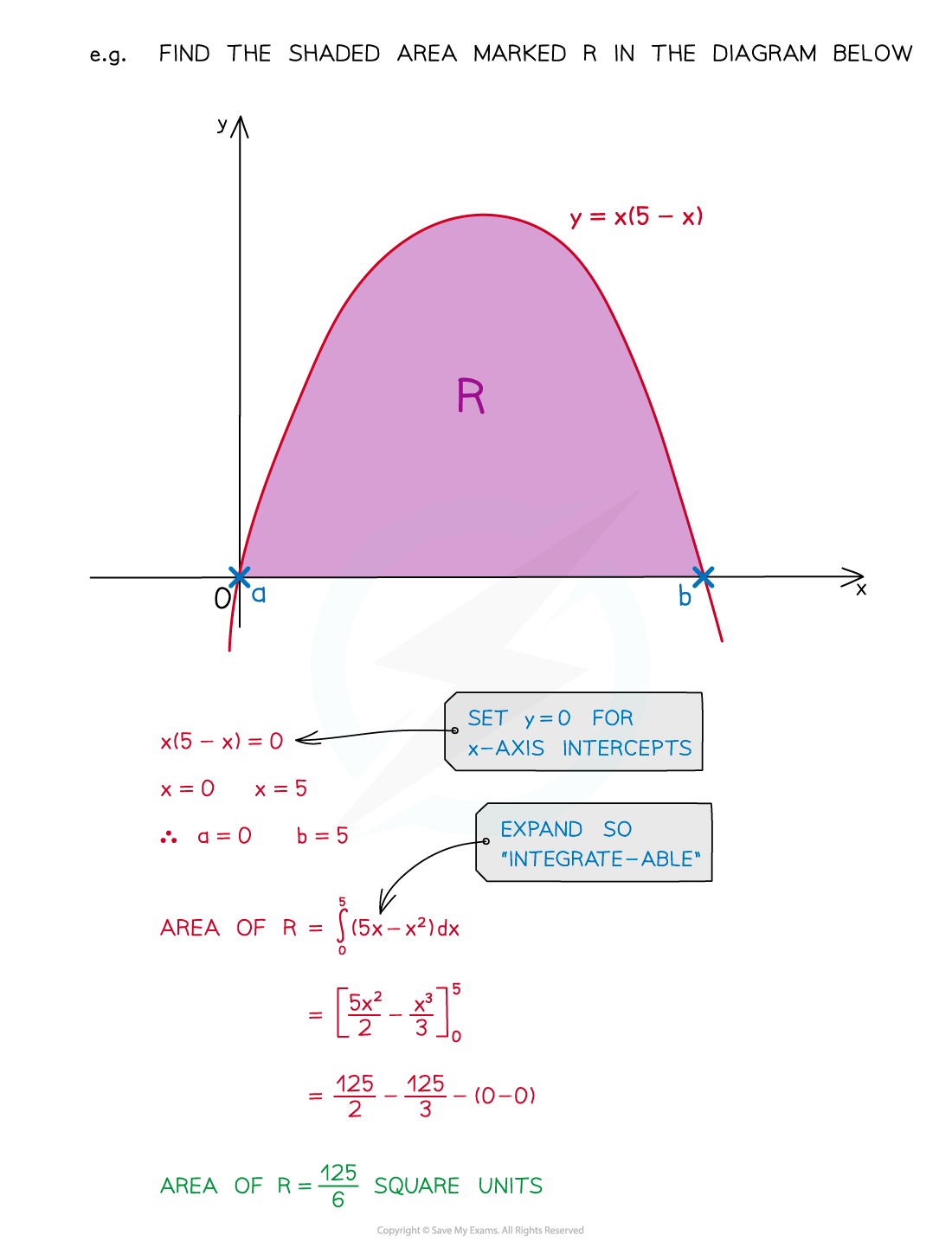
What if I am not told the limits?

If limits are not provided they will be the x-axis intercepts
Set y = 0 and solve the equation to find the x-axis intercepts
Negative areas

If the area lies underneath the x-axis the value of the integral will be negative
An area cannot be negative, so take the modulus of the integral
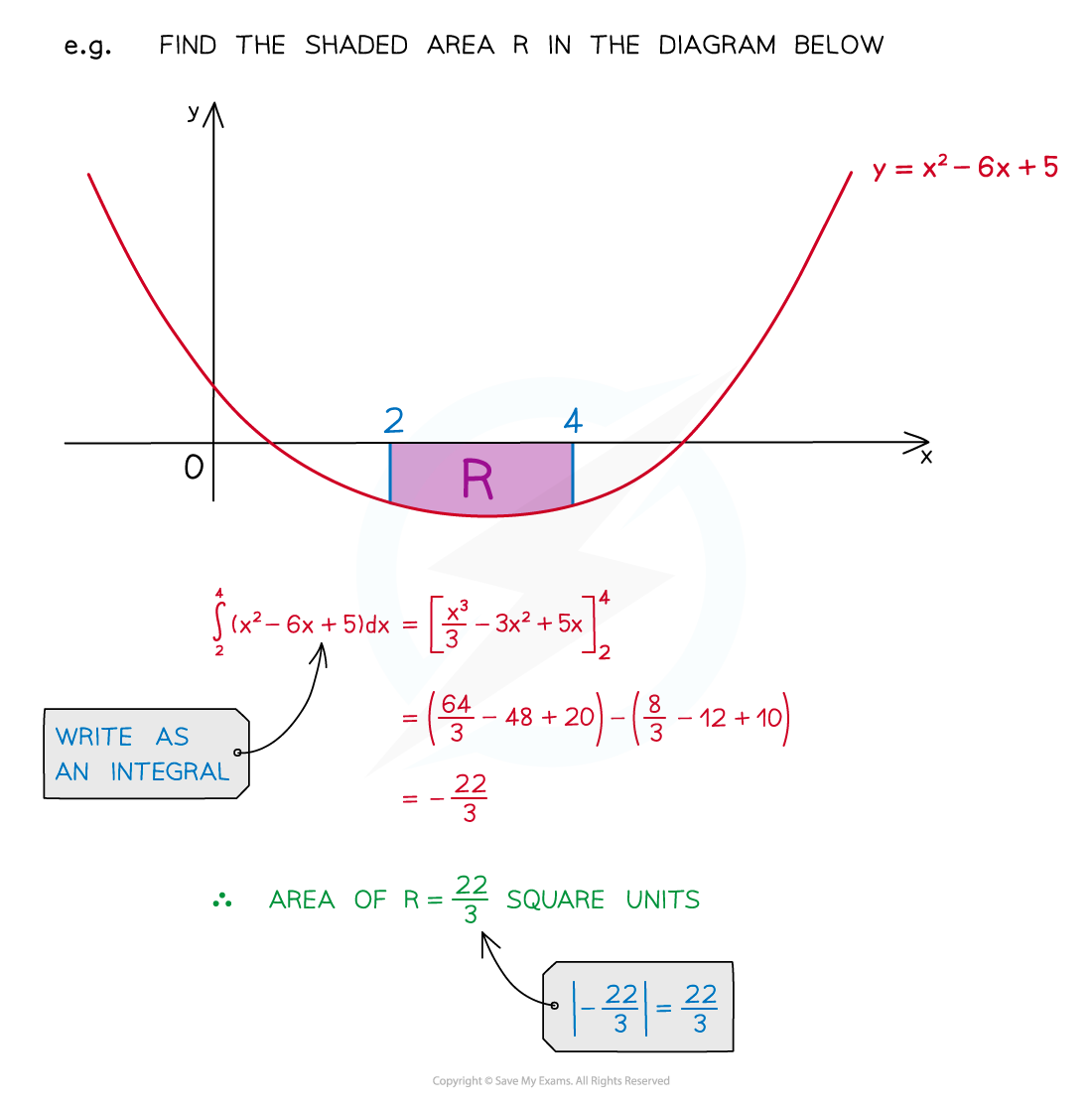
What if the area is made up of more than one section?
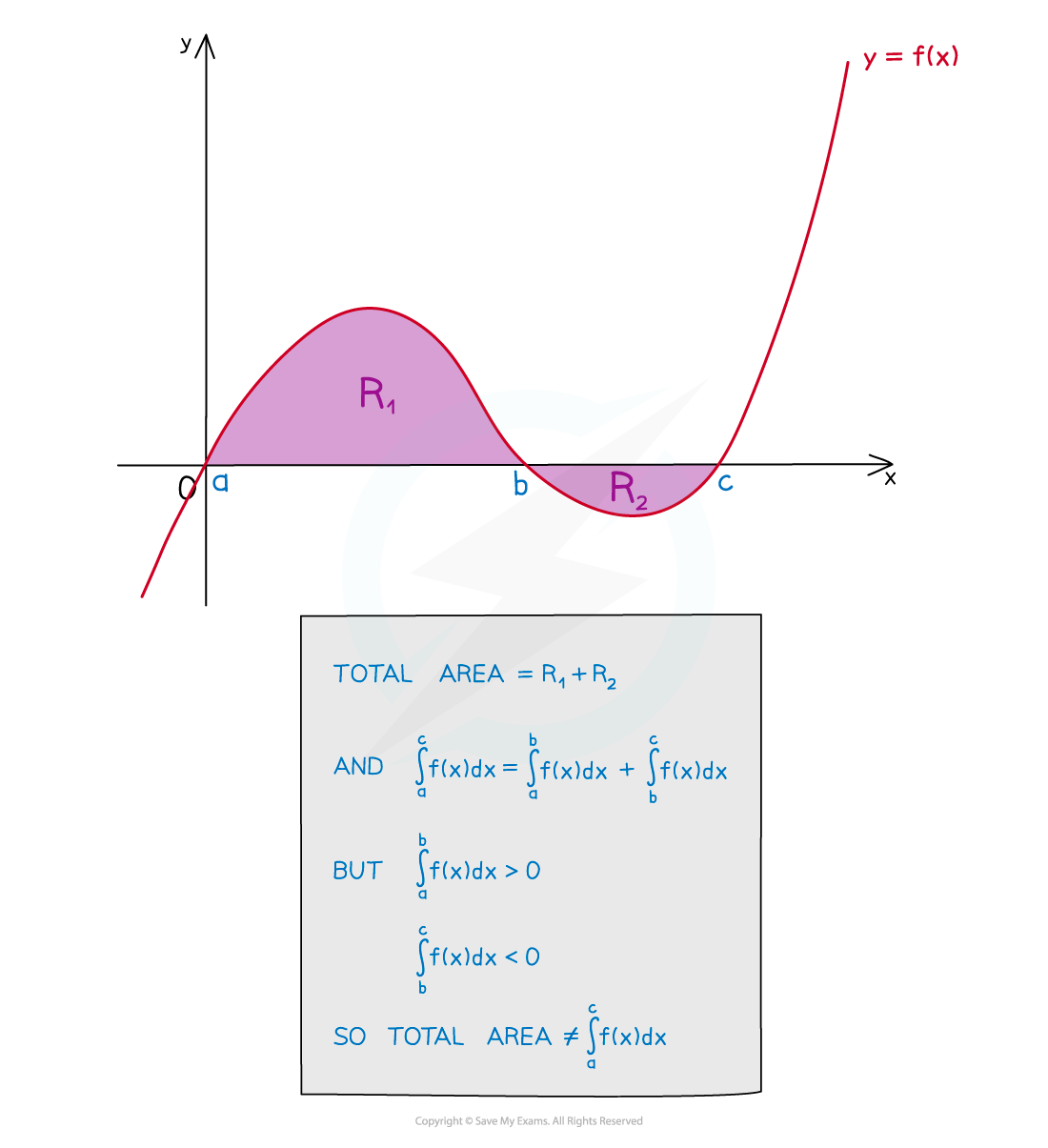
Be careful when one section is above and one section is below the x-axis
You will need a separate integral for each section, BUT...
...One section's integral will be negative
...One section's integral will be positive
So you’ll need to take the modulus before adding to find the total area
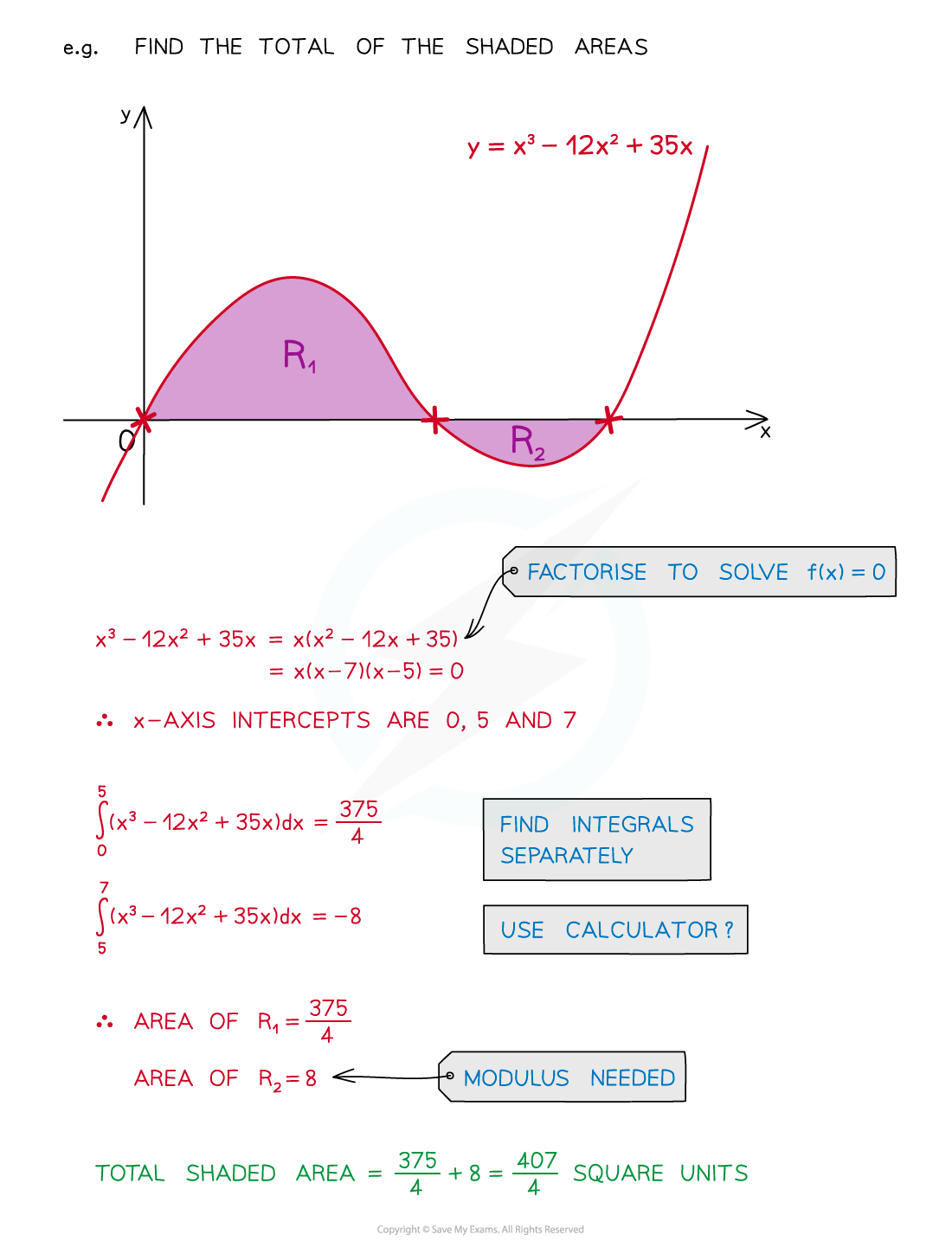
Examiner Tips and Tricks
Add information to any diagram provided in the question, as well as axes intercepts and values of limits.
Mark and shade the area you’re trying to find, and if no diagram is provided, sketch one!
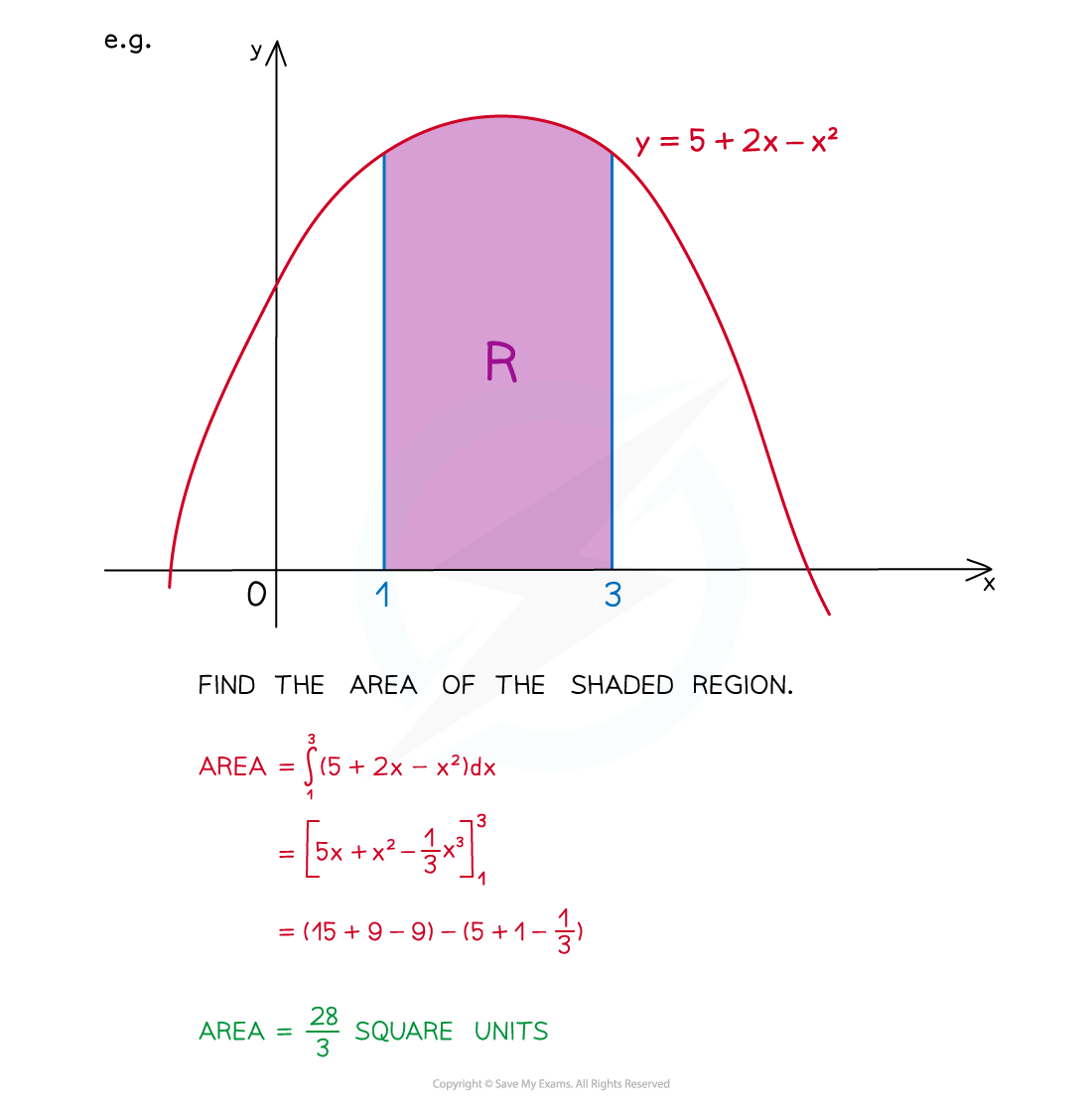
Worked Example


You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?
