Differentiating Other Functions (Edexcel A Level Maths) : Revision Note
Did this video help you?
Differentiating Other Functions (Trig, ln & e etc)
How do I differentiate common functions?
These are the common results
for
How do I differentiate exponentials and logarithms?
The two basic differentiation formulae are:

From those basic formulae are derived these two additional formulae:

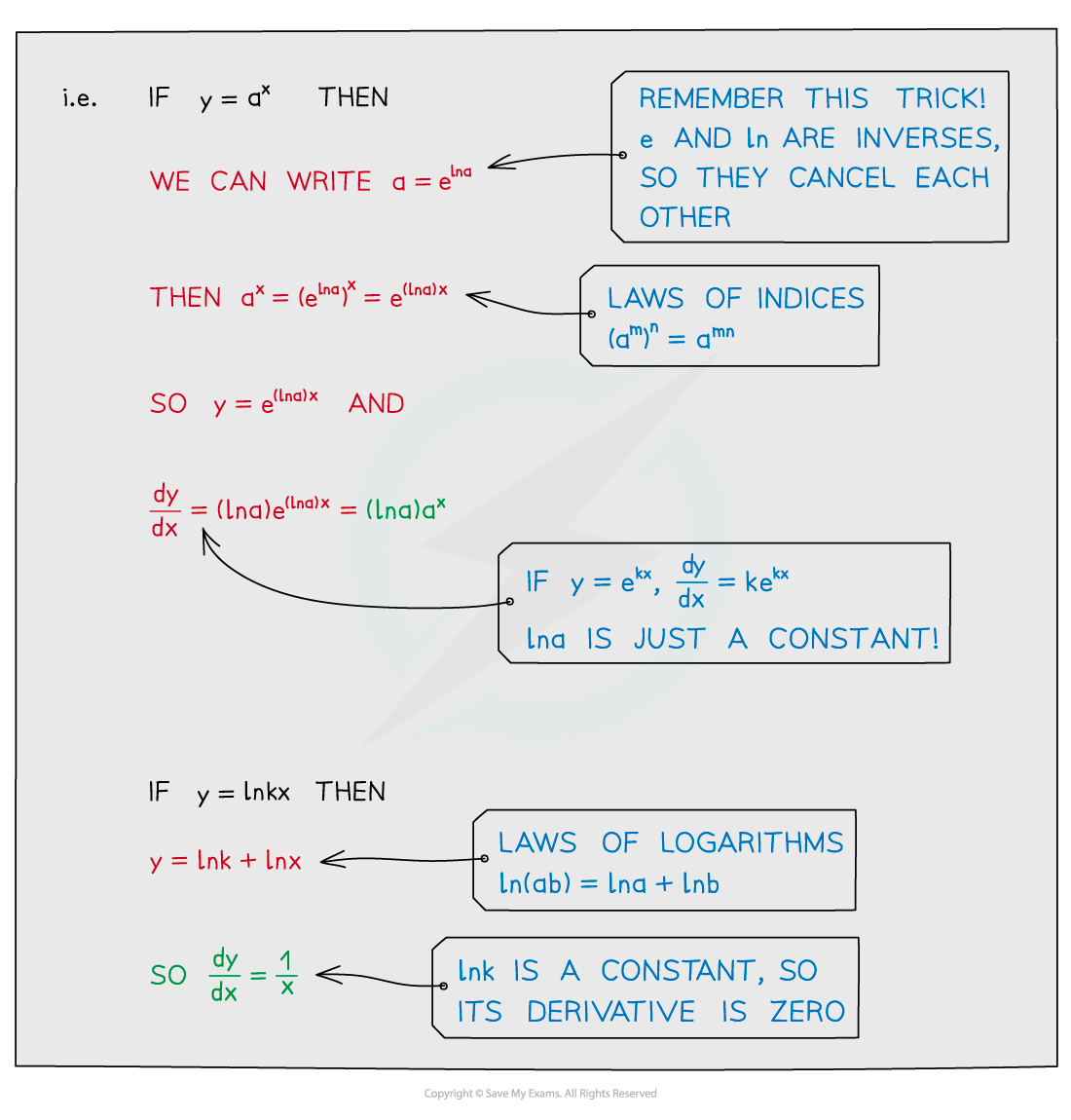
And for exponentials more generally:

This last formula can be derived from Formula 3 by using the chain rule
Examiner Tips and Tricks
The formulae for some of these derivatives are not given in the formulae booklet – you need to know them.
The formulae for ekx and ln x are the ones you absolutely do need to know .
The other formulae can be derived from those two as shown above, and remember – the derivative of ln kx is
, NOT
!
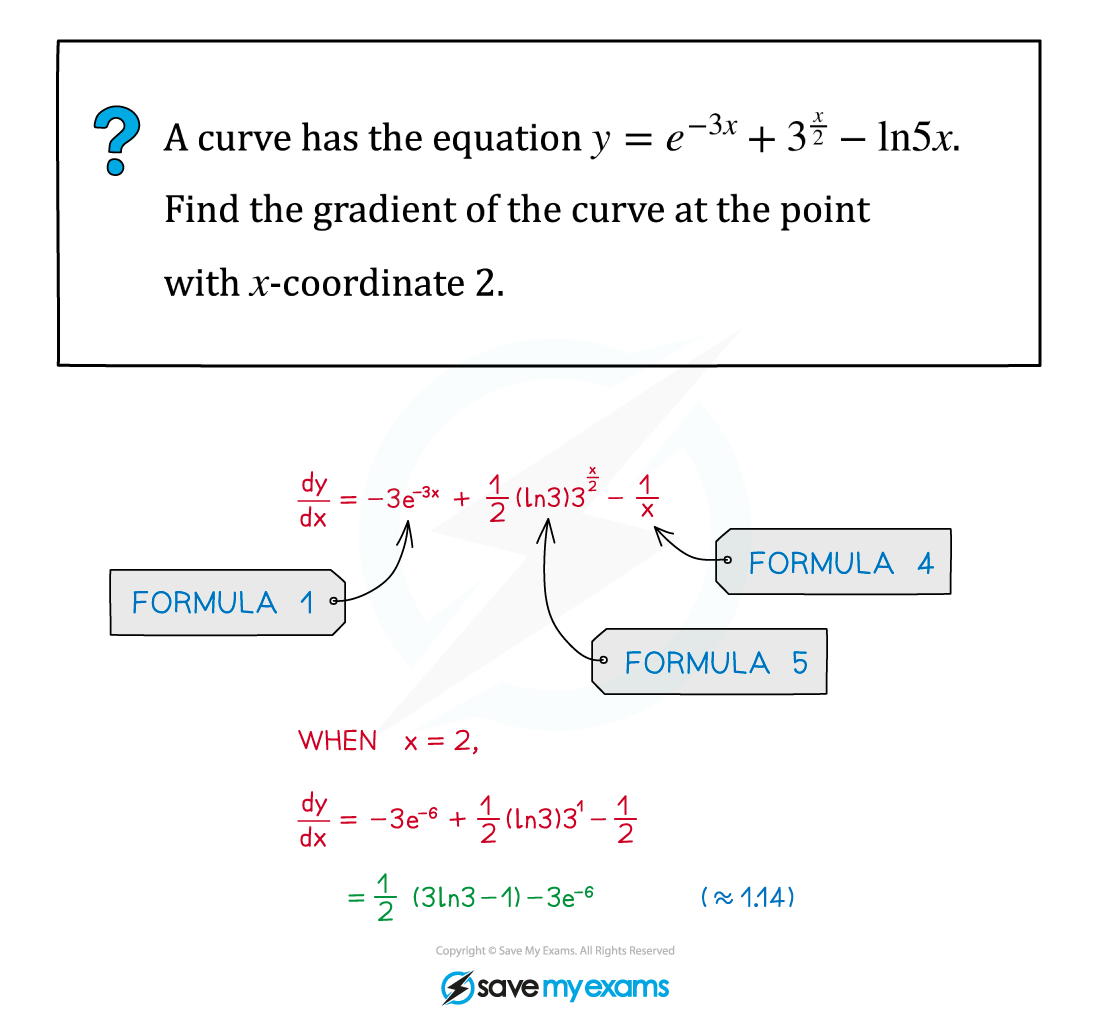
Worked Example

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
