Laws of Logarithms

Did this video help you?

Laws of Logarithms Notes fig1, A Level & AS Maths: Pure revision notes

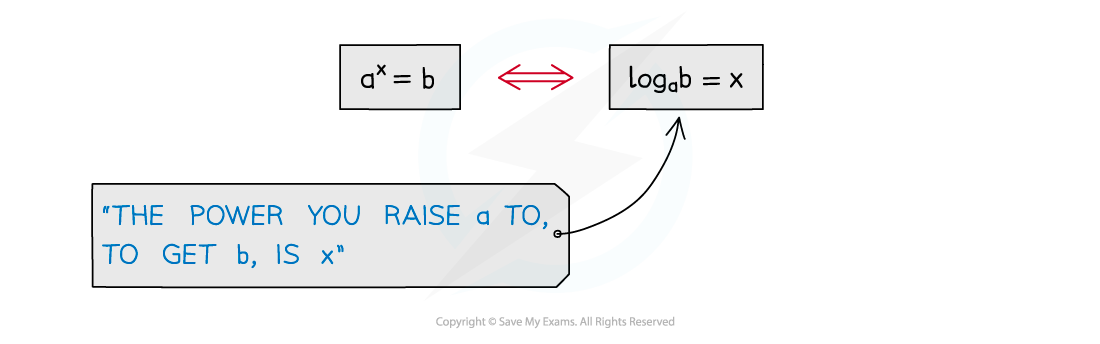
There are many laws or rules of indices, for example
- a^m x aⁿ = a^m+n
- (a^m)ⁿ = a^mn
There are equivalent laws of logarithms (for a > 0)
- $\log_{a} x y = \log_{a} x + \log_{a} y$
- $\log_{a} (\frac{x}{y}) = \log_{a} x - \log_{a} y$
- $\log_{a} x^{k} = k \log_{a} x$

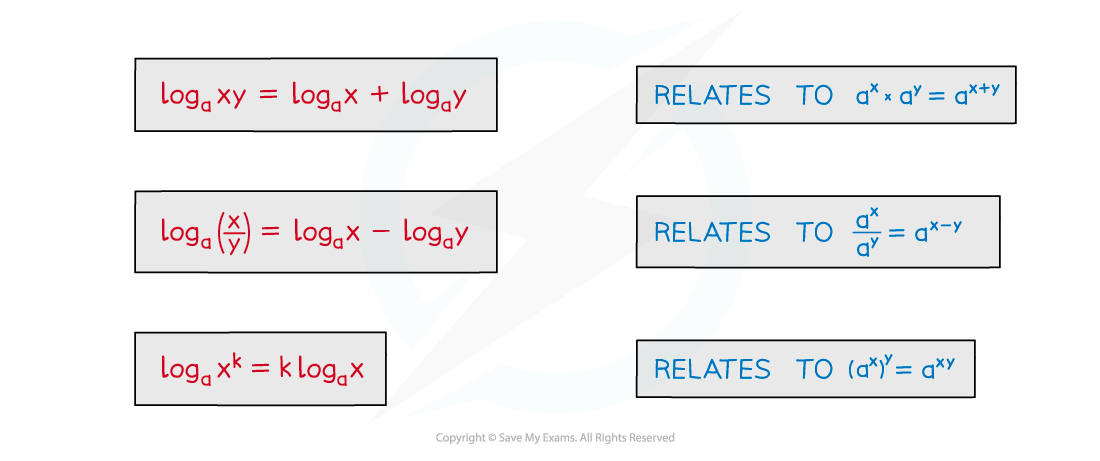
Laws of Logarithms Notes fig2, A Level & AS Level Pure Maths Revision Notes

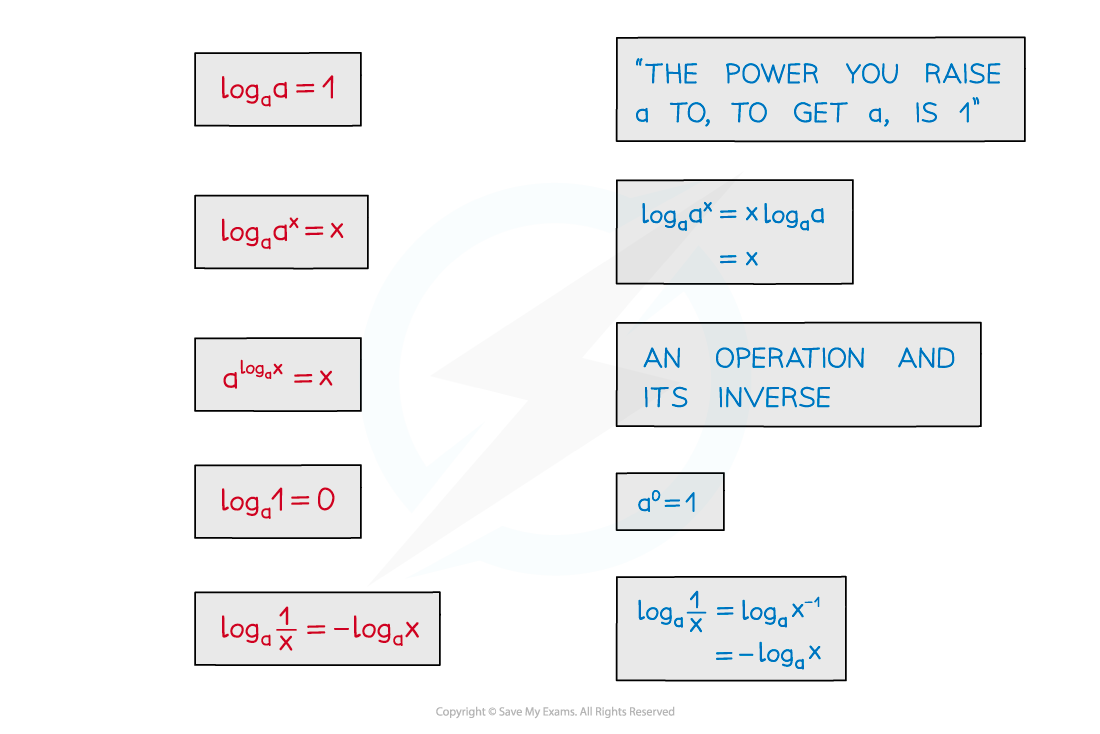
Laws of Logarithms Notes fig3, A Level & AS Level Pure Maths Revision Notes

Two of these were seen in the notes Logarithmic Functions
Beware …
- … log (x + y) ≠ log x + log y
Results apply to ln too
- $\ln x \equiv \log_{e} x$
- In particular $e^{\ln x} = x$ and $\ln (e^{x}) = x$

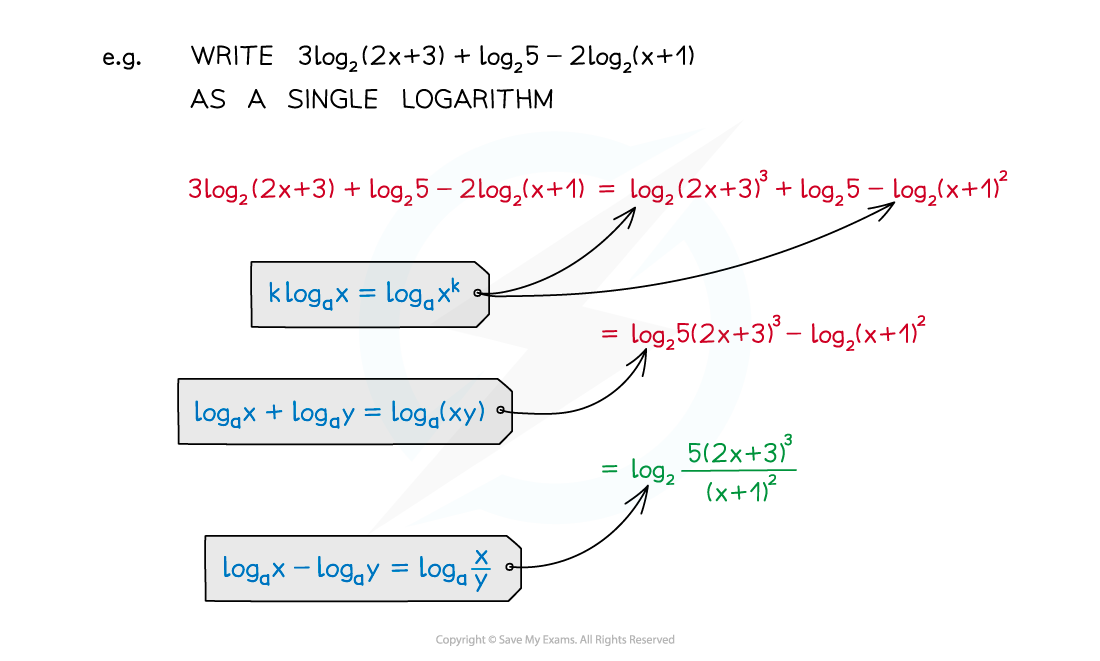
Laws of logarithms can be used to …
- … simplify expressions
- … solve logarithmic equations
- … solve exponential equations

Remember to check whether your solutions are valid
- log (x+k) is only defined if x > -k
- You will lose marks if you forget to reject invalid solutions

Laws of Logarithms Example fig1, A Level & AS Level Pure Maths Revision Notes

Did this video help you?

"ln"

ln is a function that stands for natural logarithm
It is a logarithm where the base is the constant "e"
- $\ln x \equiv \log_{e} x$
- It is important to remember that ln is a function and not a number

Using the definition of a logarithm you can see
- $\ln 1 = 0$
- $\ln e = 1$
- $\ln e^{x} = x$
- $\ln x$ is only defined for positive x
As ln is a logarithm you can use the laws of logarithms
- $\ln a + \ln b = \ln (a b)$
- $\ln a - \ln b = \ln (\frac{a}{b})$
- $n \ln a = \ln (a^{n})$

The functions $e^{x}$ and $\ln x$ are inverses of each other
- If $e^{f (x)} = g (x)$ then $f (x) = \ln g (x)$
- If $\ln f (x) = g (x)$ then $f (x) = e^{g (x)}$
If your equation involves "e" then try to get all the "e" terms on one side
- If "e" terms are multiplied, you can add the powers
  - $e^{x} \times e^{y} = e^{x + y}$
  - You can then apply ln to both sides of the equation
- If "e" terms are added, try transforming the equation with a substitution
  - For example: If $y = e^{x}$ then $e^{4 x} = y^{4}$
  - You can then solve the resulting equation (usually a quadratic)
  - Once you solve for y then solve for x using the substitution formula
If your equation involves "ln", try to combine all "ln" terms together
- Use the laws of logarithms to combine terms into a single term
- If you have $\ln f (x) = \ln g (x)$ then solve $f (x) = g (x)$
- If you have $\ln f (x) = k$ then solve $f (x) = e^{k}$

3-1-1-ln-we-solution

Always simplify your answer if you can
- for example, $\frac{1}{2} \ln 25 = \ln \sqrt{25} = \ln 5$
- you wouldn't leave your final answer as $\sqrt{25}$ so don't leave your final answer as $\frac{1}{2} \ln 25$