Geometric Series (Edexcel A Level Maths) : Revision Note
Did this video help you?
Geometric Series
How do I find the sum of a geometric series?
A geometric series is the sum of the terms of a geometric sequence

The following formulae will let you find the sum of the first n terms of a geometric series:
or
a is the first term
r is the common ratio
The one on the left is more convenient if r < 1, the one on the right is more convenient if r > 1
The a and the r in those formulae are exactly the same as the ones used with geometric sequences
How do I prove the geometric series formula?
Learn this proof of the geometric series formula – you can be asked to give it in the exam:
Write out the sum once
Write out the sum again but multiply each term by r
Subtract the second sum from the first
All the terms except two should cancel out
Factorise and rearrange to make S the subject

What is the sum to infinity of a geometric series?
If (and only if!) |r| < 1, then the geometric series converges to a finite value given by the formula
S∞ is known as the sum to infinity
If |r| ≥ 1 the geometric series is divergent and the sum to infinity does not exist
Examiner Tips and Tricks
The geometric series formulae are in the formulae booklet – you don't need to memorise them
You will sometimes need to use logarithms to answer geometric series questions (see Exponential Equations)
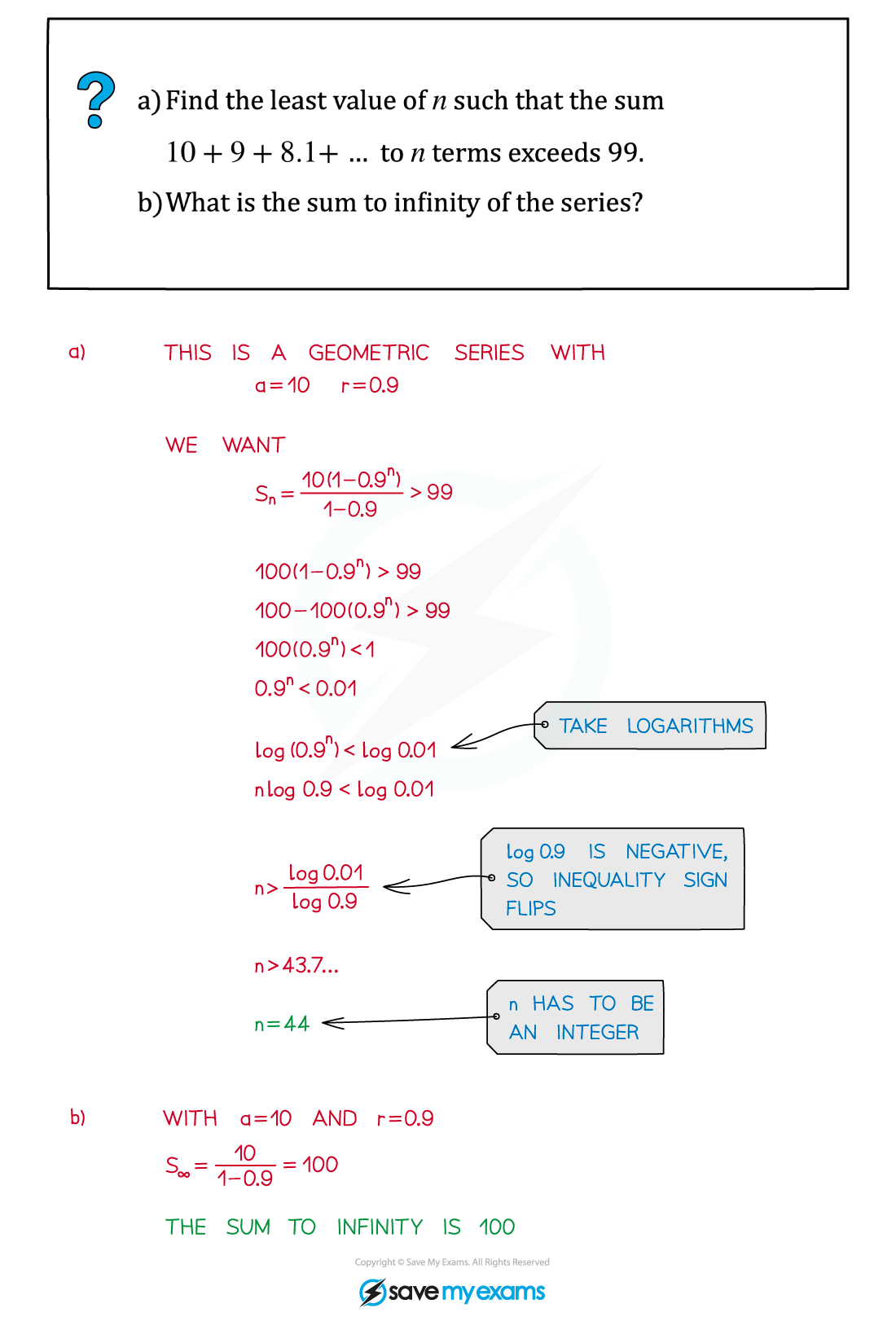
Worked Example

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?
