Sketching Polynomials (Edexcel A Level Maths: Pure)

Sketching the graph of a polynomial

• Remember a polynomial is any finite function with non-negative indices, that could mean a quadratic, cubic, quartic or higher power

 

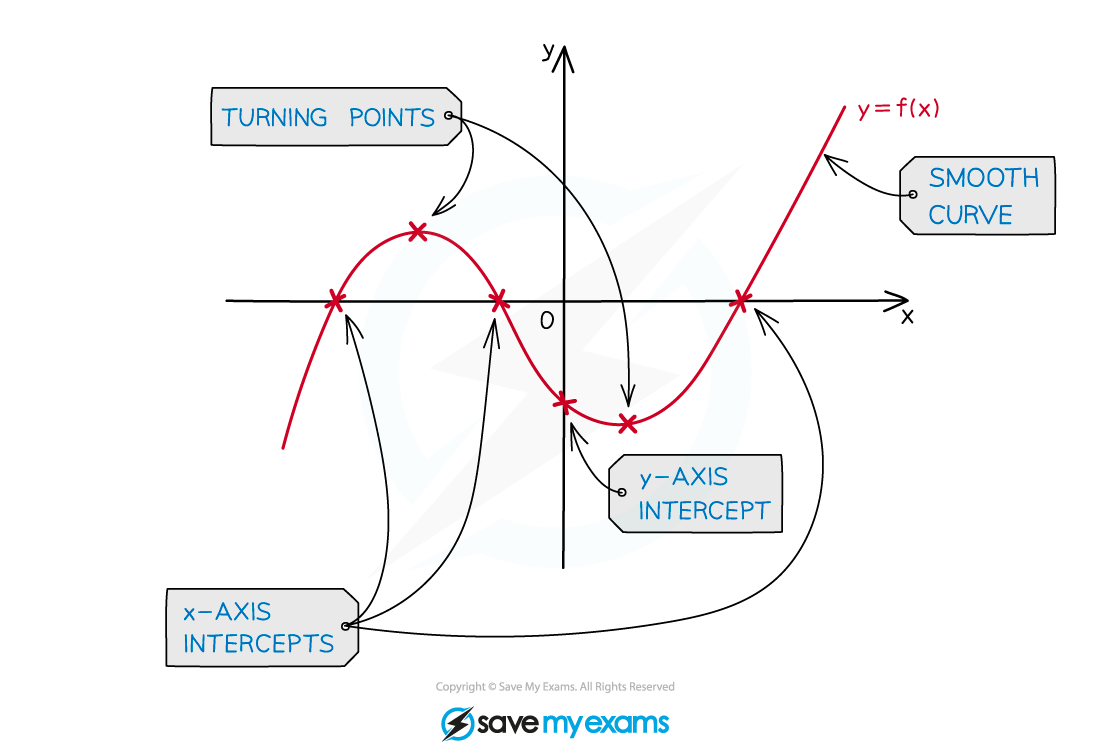
• When asked to sketch a polynomial you'll need to think about the following
  • y-axis intercept
  • x-axis intercepts (roots)
  • turning points (maximum and/or minimum)
  • a smooth curve (this takes practice!)

How do I sketch a graph of a polynomial?

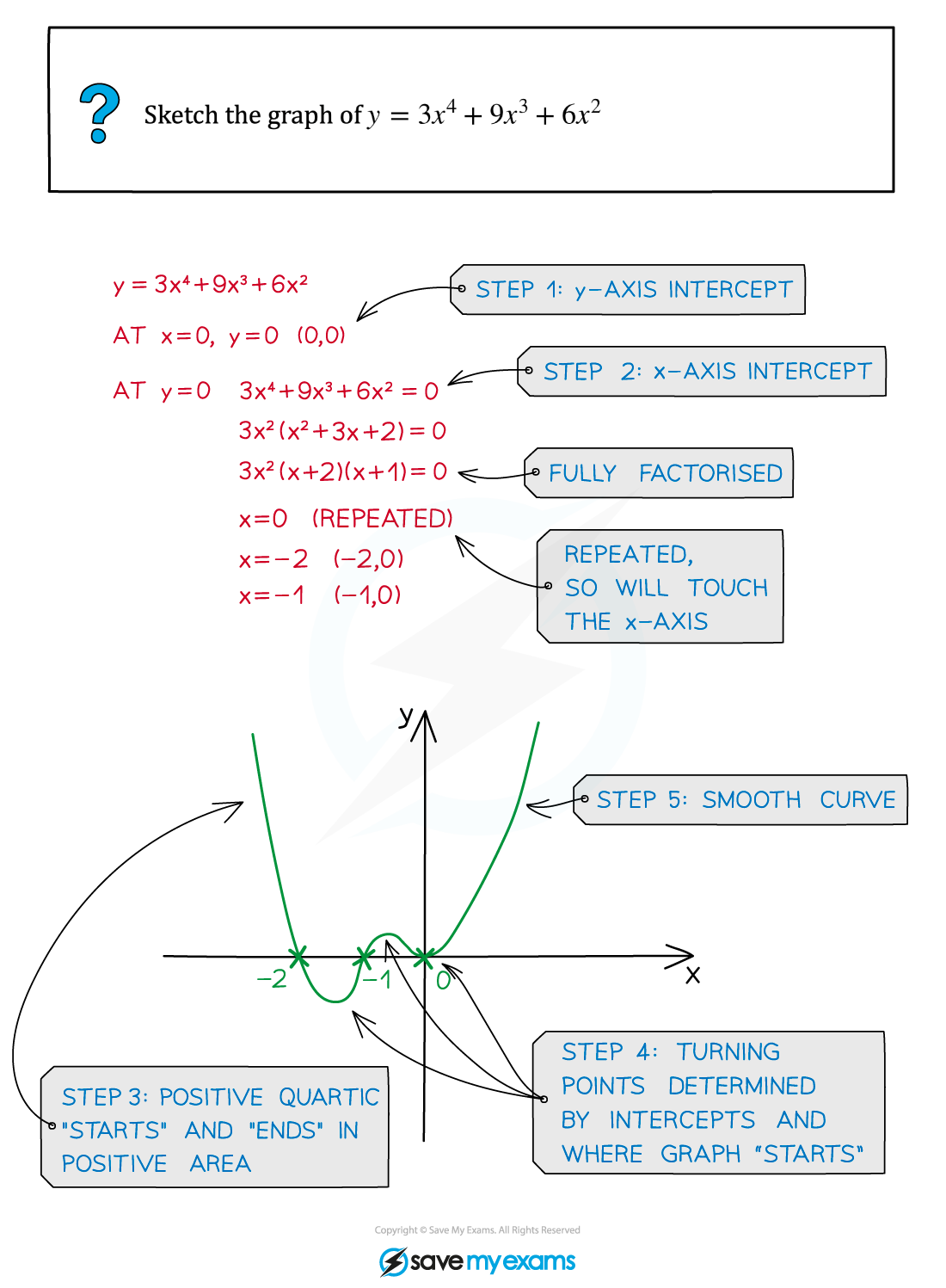
STEP 1        Find the y-axis intercept by setting x = 0

STEP 2        Find the x-axis intercepts (roots) by setting y = 0

STEP 3        Consider the shape and “start”/”end” of the graph

eg. a positive cubic graph starts in third quadrant (“bottom left”) and “ends” in first quadrant (“top right”)

STEP 4        Consider where any turning points should go

STEP 5        Draw with a smooth curve

 

• Coordinates of turning points can be found using differentiation
• Except with a point of inflection, repeated roots indicate the graph touches the x-axis