Factorisation (Edexcel A Level Maths) : Revision Note
Did this video help you?
Polynomial Factorisation
What is polynomial factorisation?
Factorising a polynomial combines the factor theorem with the method of polynomial division
The goal is to break down a polynomial as far as possible into a product of linear factors

How do I factorise a polynomial?
At A level you will usually be asked to factorise a cubic – i.e. a polynomial where the highest power of x is 3
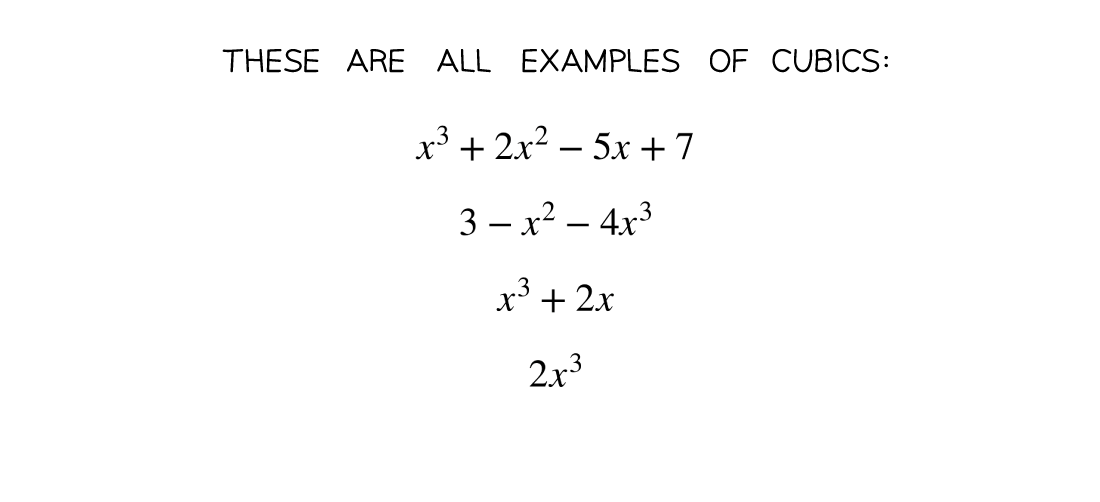
To factorise a cubic polynomial f(x) follow the following steps:
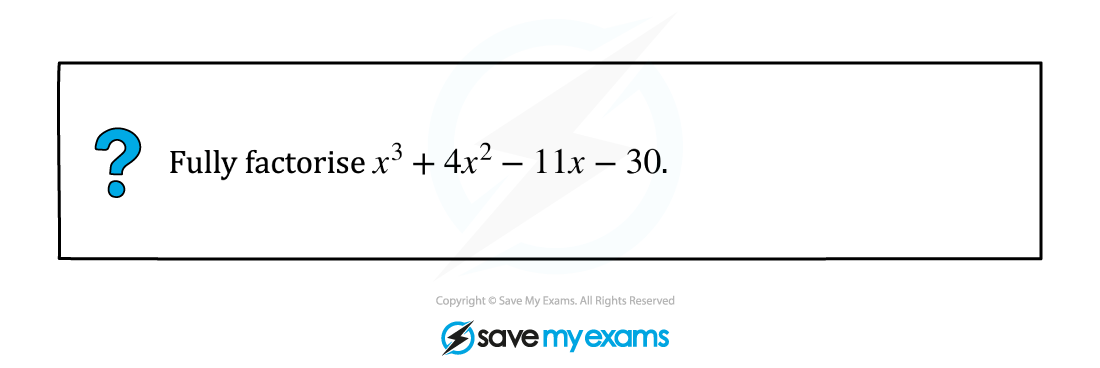
Step 1. Find a value p that makes f(p) = 0

Step 2. Use polynomial division to divide f(x) by (x - p)

Step 3. Use the result of your division to write
f(x) = (x - p) (ax2 + bx + c)
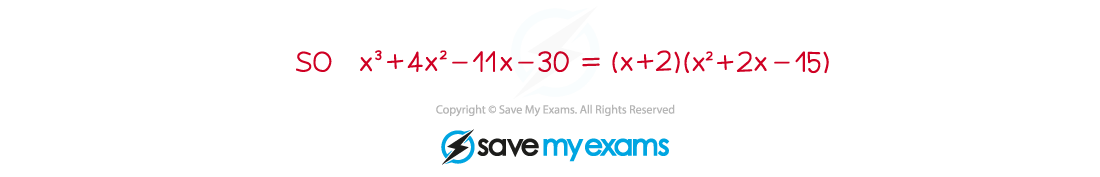
Step 4. If the quadratic (ax2 + bx + c) is factorisable, factorise it and write f(x) as a product of three linear factors (if the quadratic is not factorisable, then your result from Step 3 is the final factorisation)

Examiner Tips and Tricks
The method outlined above can be logically extended to factorise a polynomial of any degree.
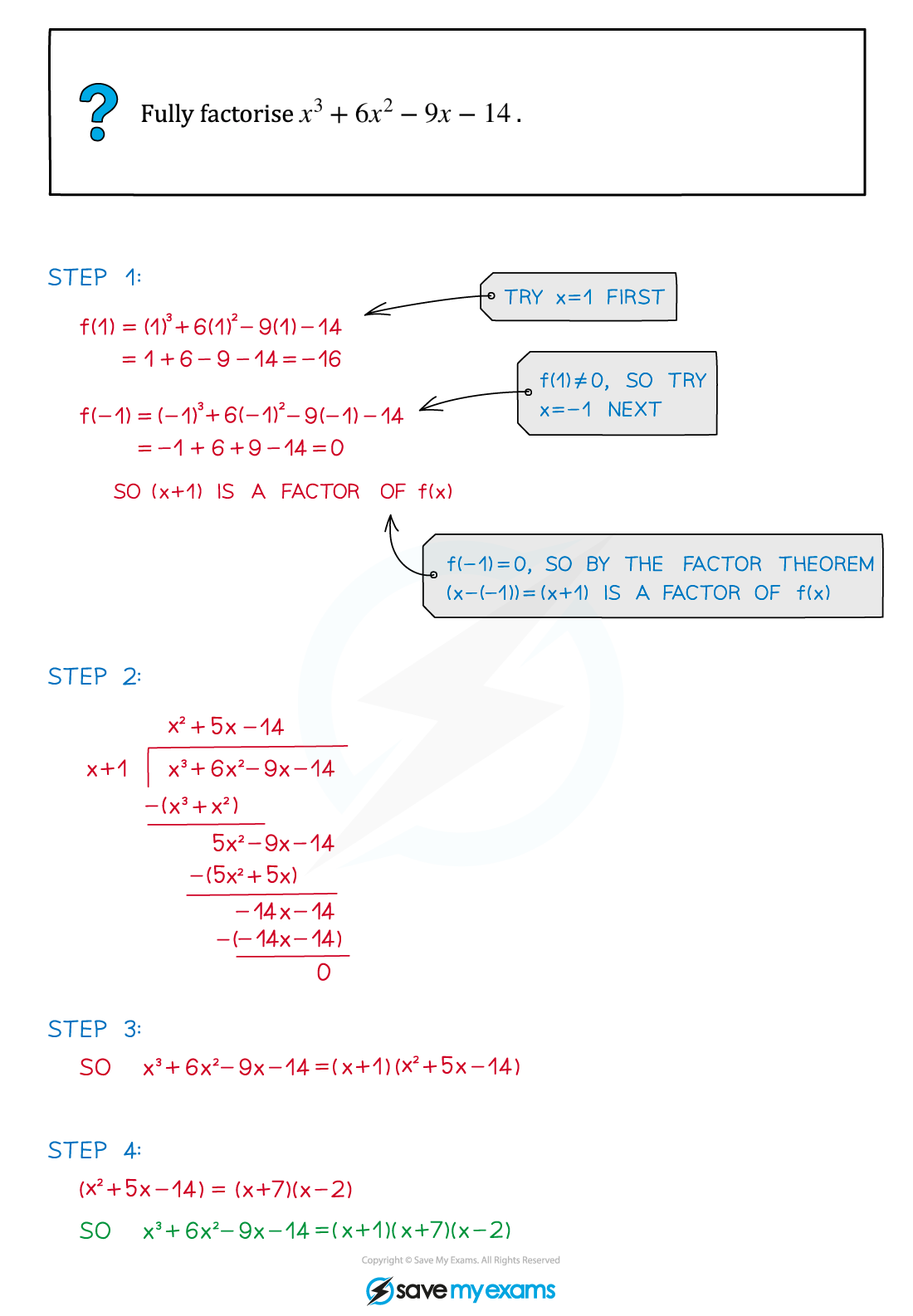
Worked Example

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?
