A LevelMaths: PureEdexcelRevision Notes11. Vectors11.1 Vectors in 2 Dimensions11.1.4 Position Vectors

Position Vectors (Edexcel A Level Maths: Pure)

Revision Note

Test yourself
Lucy

Author

Lucy

Last updated

Did this video help you?

Position Vectors

What is a position vector?

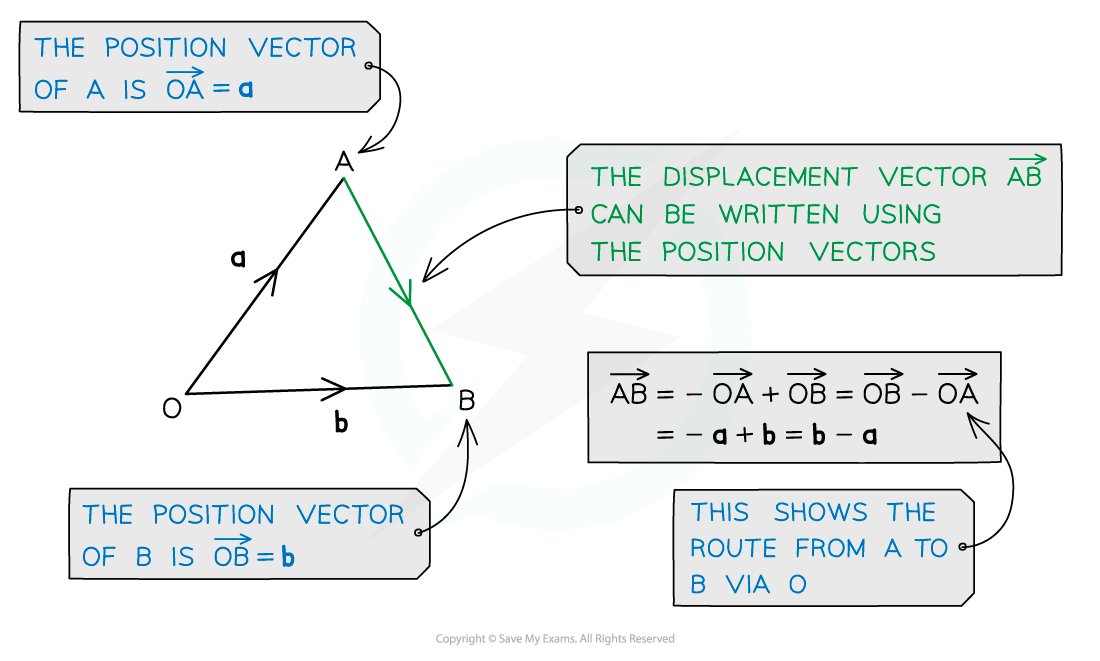
  • Position vectors describe the position of a point in relation to the origin
  • They are different to displacement vectors which describe the direction and distance between any two points

 

new-11-1-4-position-vectors-diagram-1

Distance between two points

  • The distance between two points is the magnitude of the vector between them (see Magnitude Direction)

 Position Vectors Diagram 2a, AS & A Level Maths revision notes

How do I find the magnitude of a displacement vector?

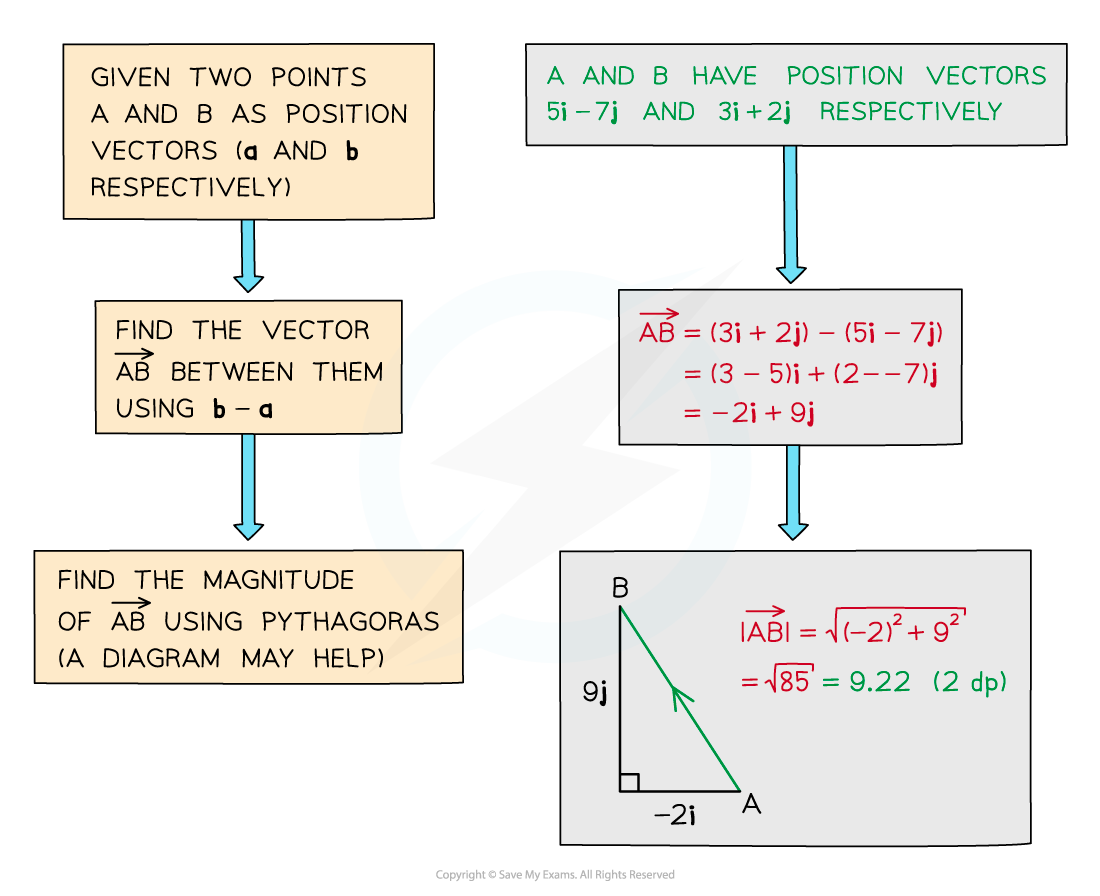
  • You can use coordinate geometry to find magnitudes of displacement vectors from A  to B
    • From the position vectors of A  and B  you know their coordinates
      • If  bold a equals stack O A with rightwards arrow on top equals x subscript 1 bold i plus y subscript 1 bold j equals open parentheses table row cell x subscript 1 end cell row cell y subscript 1 end cell end table close parentheses,  then point A has coordinates open parentheses x subscript 1 comma space y subscript 1 close parentheses
      • If  bold b equals stack O B with rightwards arrow on top equals x subscript 2 bold i plus y subscript 2 bold j equals open parentheses table row cell x subscript 2 end cell row cell y subscript 2 end cell end table close parentheses,  then point B has coordinates open parentheses x subscript 2 comma space y subscript 2 close parentheses
    • The distance between two points is given by d space equals blank square root of open parentheses x subscript 1 minus blank x subscript 2 close parentheses squared space plus space open parentheses y subscript 1 minus blank y subscript 2 close parentheses squared end root blank
      • So  open vertical bar stack A B with rightwards arrow on top close vertical bar space equals blank square root of open parentheses x subscript 1 minus blank x subscript 2 close parentheses squared space plus space open parentheses y subscript 1 minus blank y subscript 2 close parentheses squared end root blank
    • For example, if points A and B have position vectors 5 bold i plus 3 bold j and 3 bold i minus 6 bold j respectively
      • then  open vertical bar stack A B with rightwards arrow on top close vertical bar equals square root of open parentheses 5 minus 3 close parentheses squared plus open parentheses 3 minus open parentheses negative 6 close parentheses close parentheses squared end root equals square root of 85 equals 9.22 space open parentheses 3 space straight s. straight f. close parentheses

  • Alternatively, you could find open vertical bar stack A B with rightwards arrow on top close vertical bar by
    • first using  stack A B with rightwards arrow on top equals negative stack O A with rightwards arrow on top plus stack O B with rightwards arrow on top to find stack A B with rightwards arrow on top in vector form
      • and then calculating its magnitude directly
    • See the Worked Example below 

Examiner Tip

  • Remember if asked for a position vector, you must find the vector all the way from the origin.
  • Diagrams can help, if there isn’t one, draw one.

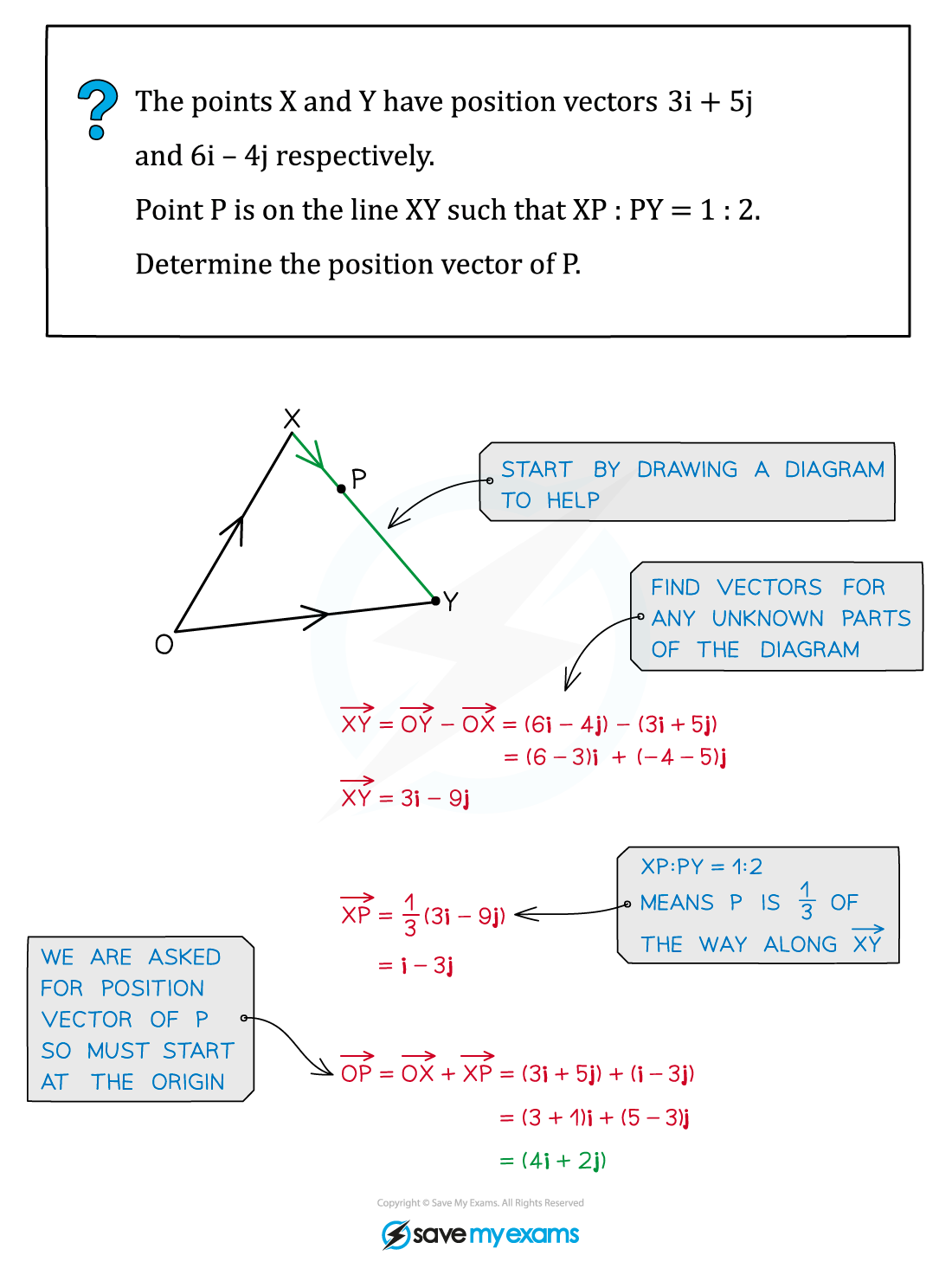
Worked example

Position Vectors Example Solution, AS & A Level Maths revision notes

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfNext topic

    Did this page help you?

    Lucy

    Author: Lucy

    Expertise: Head of STEM

    Lucy has been a passionate Maths teacher for over 12 years, teaching maths across the UK and abroad helping to engage, interest and develop confidence in the subject at all levels. Working as a Head of Department and then Director of Maths, Lucy has advised schools and academy trusts in both Scotland and the East Midlands, where her role was to support and coach teachers to improve Maths teaching for all. Lucy has created revision content for a variety of domestic and international Exam Boards including Edexcel, AQA, OCR, CIE and IB.