Inverse Functions (AQA A Level Maths) : Revision Note
Did this video help you?
Inverse Functions
What is an inverse function?
An inverse function is the opposite to the original function
An inverse function is denoted by
The inverse of a function only exists if the function is one-to-one
Inverse functions are used to solve equations
The solution of
is

Graphs of inverse functions

The graphs of a function and its inverse are reflections in the line y = x
Domain and range of inverse functions
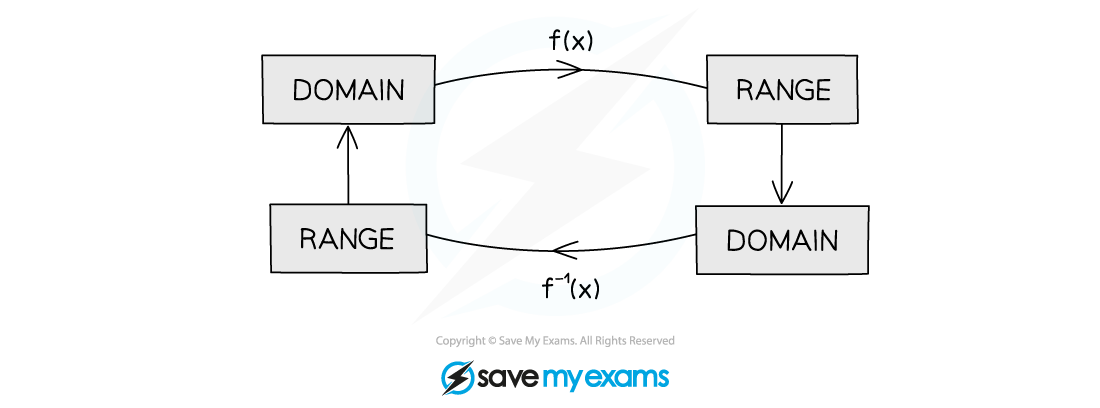
The range of a function will be the domain of its inverse function
The domain of a function will be the range of its inverse function
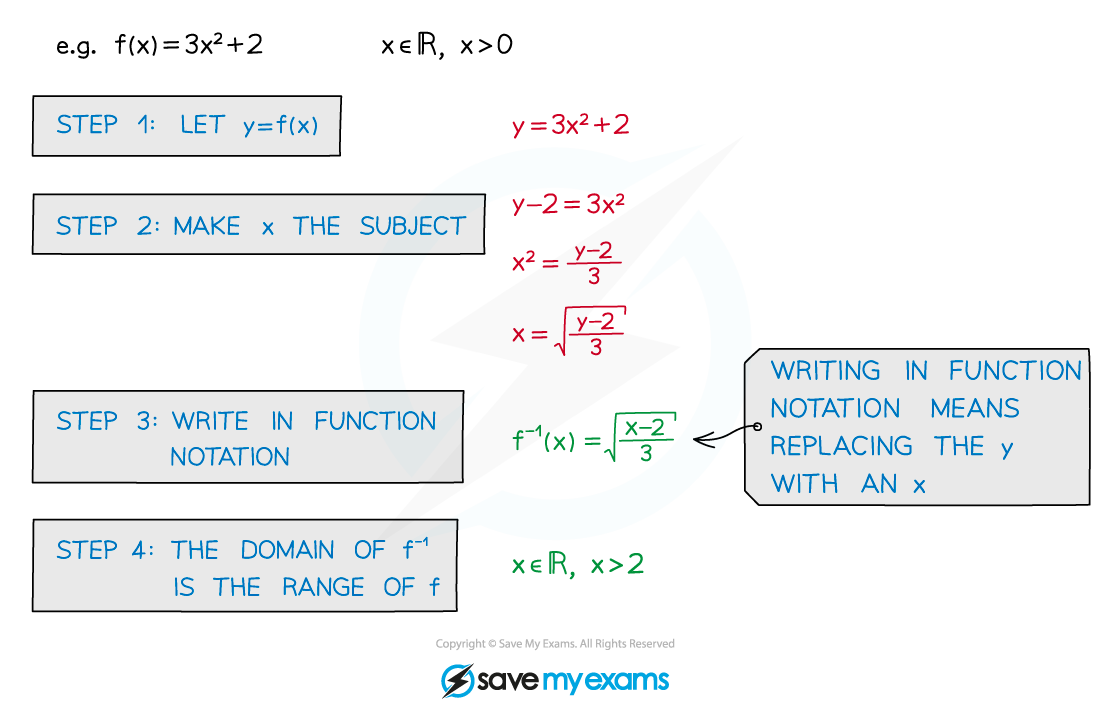
How do I work out an inverse function?
Set y = f(x) and make x the subject
Then rewrite in function notation
Domain is needed to fully define a function
The range of f is the domain of f-1 (and vice versa)
... and finally …
A function (f) followed by its inverse (f-1) will return the input (x)
ff-1(x) = f-1f(x) = x (for all values of x)

Worked Example
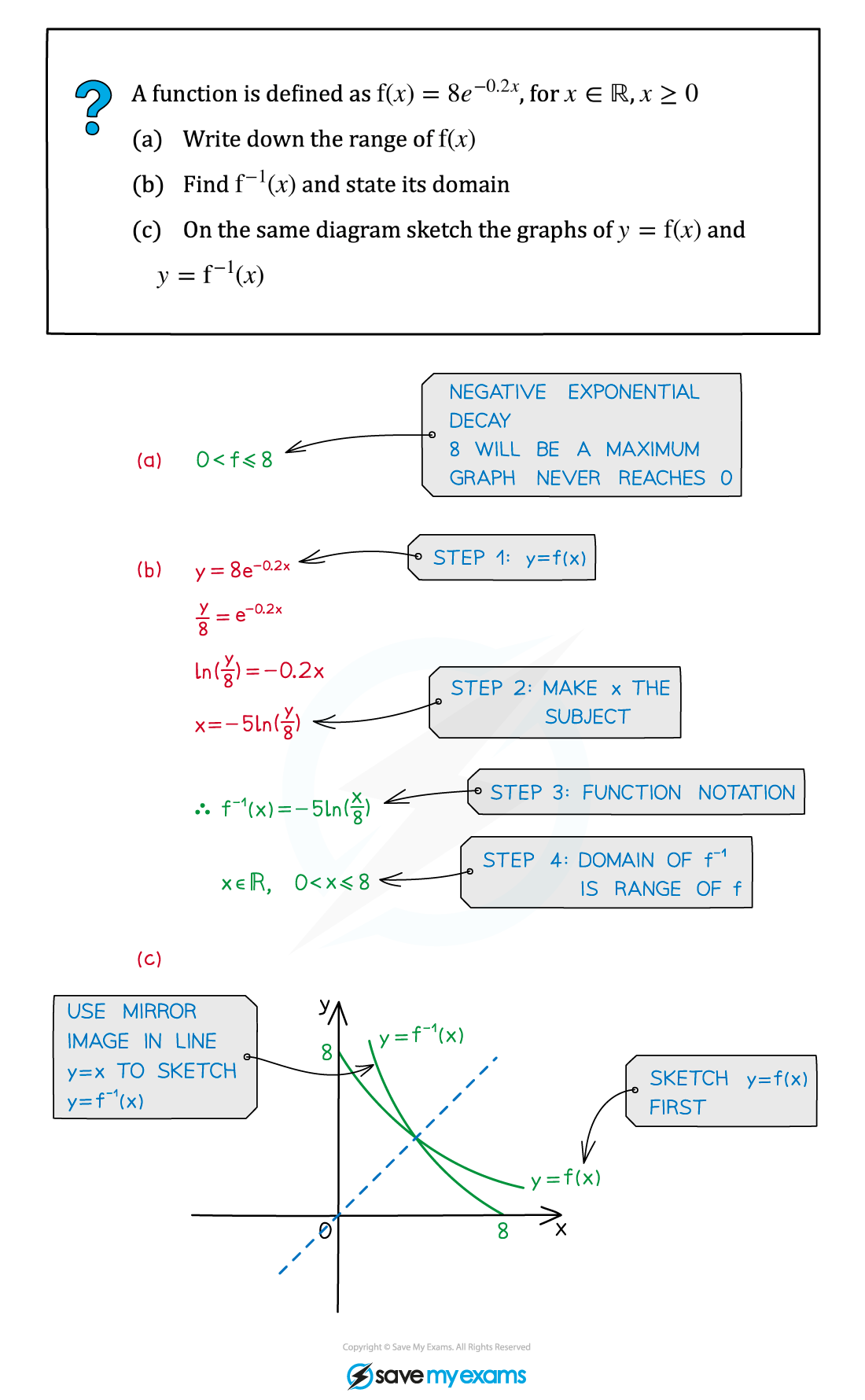

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?
