Inequalities & Regions in Argand Diagrams

How do I sketch inequalities such as $Re z < k$ or $Im z < k$ on an Argand diagram?

The inequality $Re z < 2$ is satisfied by all complex numbers, $z = x + i y$ , with a real part less than 2
- On an Argand diagram, this would be the region to the left of the vertical line $x = 2$
- The vertical line itself, $x = 2$ , should be drawn dotted to show that points on this line are not permitted due to the strict inequality (<)
In general, dotted lines are used with strict inequalities ( < or > ) and solid lines are used with inequalities that can be equal ( ≤ or ≥ )
Here is how to represent the following inequalities as regions on an Argand diagram…
- $Re z < k$ : shade the region to the left of the dotted vertical line (or solid vertical line for ≤)
- $Re z > k$ : shade the region to the right of the dotted vertical line (or solid vertical line for ≥)
Similarly, here is how to represent the following inequalities as regions on an Argand diagram…
- $Im z < k$ : shade the region below the dotted horizontal line (or solid horizontal line for ≤)
- $Im z > k$ : shade the region above the dotted horizontal line (or solid horizontal line for ≥)

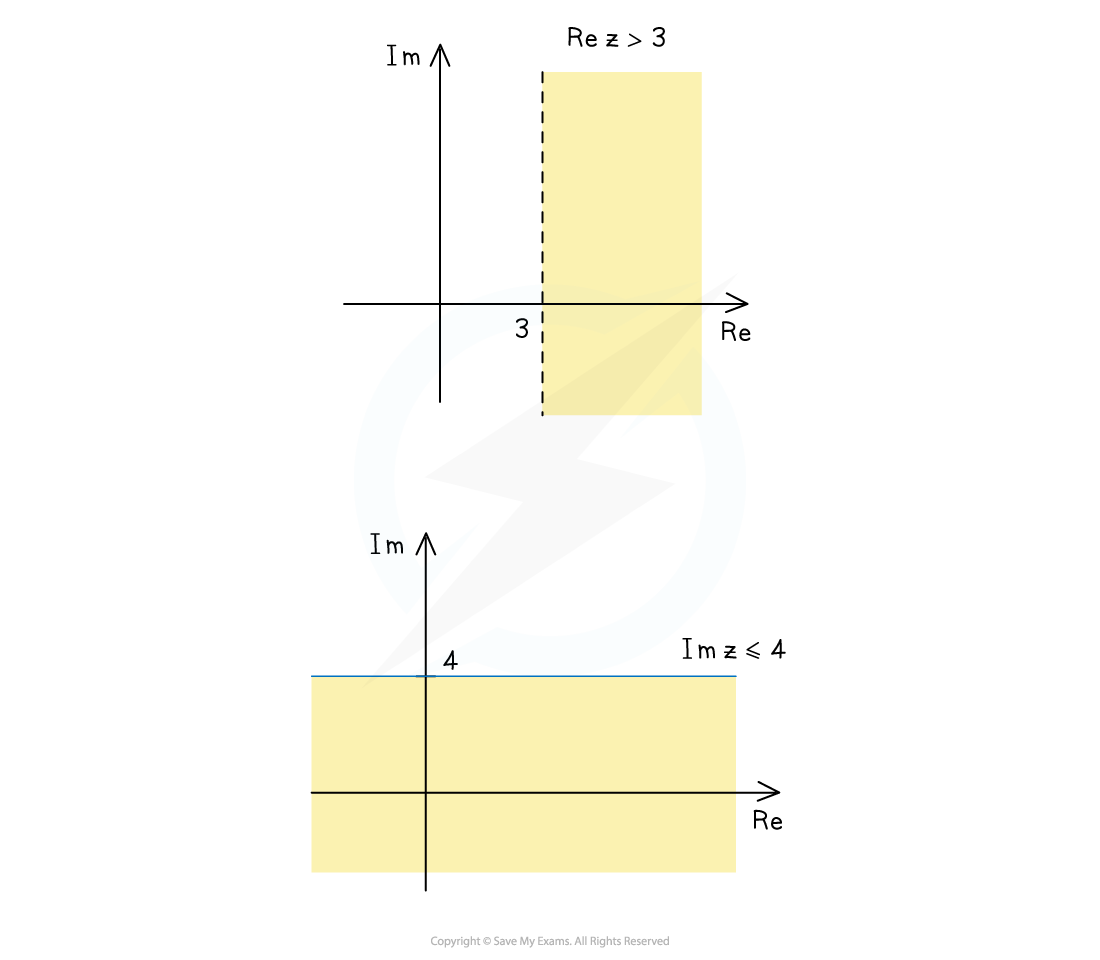
8-2-5_notes_fig1

Sketching the inequalities $Re z > 3 a n d Im z \leq 4$

How do I sketch inequalities such as $|z - a| < k$ on an Argand diagram?

For a given complex number $a$ , the inequality $|z - a| < k$ represents all complex numbers, $z$ , that lie inside the circle of radius $k$ , centred at $a$
Here is how to represent the following inequalities as regions on an Argand diagram…
- $|z - a| < k$ : shade the region inside the circle of radius $k$ , centred at $a$
- $|z - a| > k$ : shade the (unbounded) region outside circle of radius $k$ , centred at
- Again use a dotted line for strict inequalities (< and >) and a solid line for weak inequalities ( ≤ or ≥ )

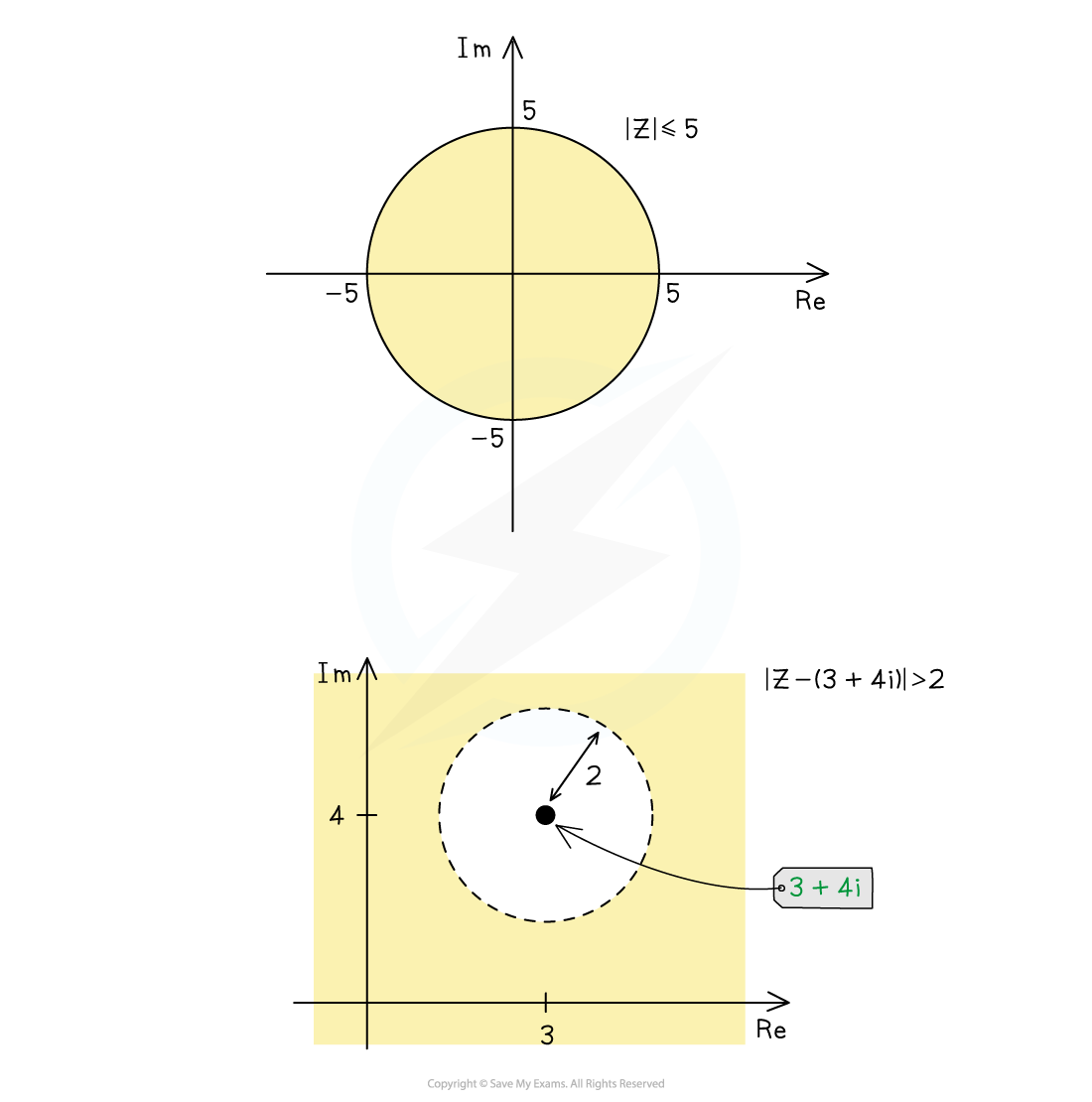
8-2-5_notes_fig2

Sketching the inequalities $| z | \leq 5$ and $| z - (3 + 4 i) | > 2$

How do I sketch inequalities such as $| z - a | < | z - b |$ on an Argand diagram?

For two given complex numbers $a$ and $b$ , the inequality $|z - a| < | z - b |$ represents all complex numbers, $z$ , that lie closer to $a$ than to $b$
Here is how to represent the following inequalities as regions on an Argand diagram…
- $| z - a | < | z - b |$ : shade the region on the side of the perpendicular bisector of $a$ and $b$ that includes the point $a$
- $| z - a | > | z - b |$ : shade the region on the side of the dotted perpendicular bisector of $a$ and $b$ that includes the point $b$
A good way to remember which side to shade is that the inequality sign points (like an arrow) to the side to be shaded

Sketching the inequalities $| z - 2 | < | z - 2 i |$ and $| z - i | \geq | z - (3 + 4 i) |$

How do I sketch inequalities such as $α < \arg (z - a) < β$ on an Argand diagram?

For a given complex number, $a$ , the inequality $α < \arg (z - a) < β$ represents all complex numbers, $z$ , that have an argument between $α$ and $β$ , as measured from the point $α$
Here is how to represent the following inequalities as regions on an Argand diagram…
- $α < \arg (z - a) < β$ : shade the wedge-shaped region between the half-line $\arg (z - a) = α$ and the half-line $\arg (z - a) = β$ , with an open circle at $z = a$ to show the exclusion of this point (to avoid the undefined value of $\arg 0$ )

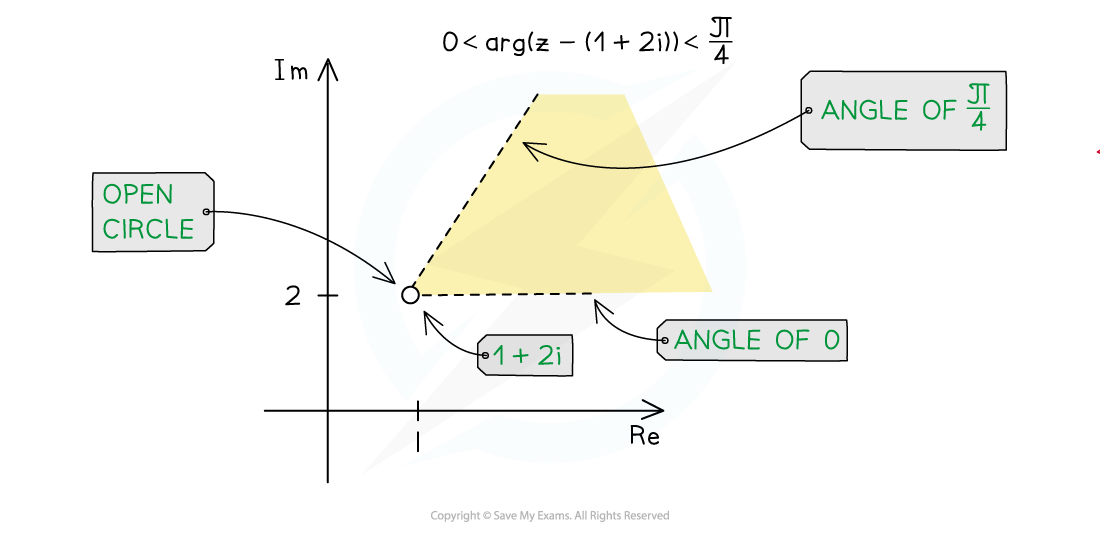
8-2-5_notes_fig4

Sketching the inequalities $0 < \arg (z - (1 + 2 i)) < \frac{π}{4}$

How do I draw multiple inequalities on the same Argand diagram?

To sketch a region that satisfies multiple inequalities, we need to find the intersection of all the regions (where all regions overlap)
- E.g. the region satisfied by $2 < |z| \leq 5$ can be found as follows…
  - Using diagonal lines in the same direction, lightly shade the region $| z | > 2$ (the outside of a circle of radius 2 about the origin)
  - Using diagonal lines in a different direction, lightly shade the region $|z| \leq 5$ (the inside of a circle of radius 5 about the origin)
  - Where the diagonal lines cross each other highlights the region satisfying both inequalities; this should be shaded boldly
- E.g. the region satisfied by $|z - i| < | z - 1 |$ and $0 \leq \arg z \leq \frac{3 π}{4}$ can be found as follows…
  - Using diagonal lines in the same direction, lightly shade the region $|z - i| < | z - 1 |$ (the side including $z = i$ from the perpendicular bisector of the points $i$ and 1)
  - Using diagonal lines in a different direction, lightly shade the region $0 \leq \arg z \leq \frac{3 π}{4}$ (the wedge-shaped region from 0 to $\frac{3 π}{4}$ radians from the origin)
  - Where the diagonal lines cross each other highlights the region satisfying both inequalities; this should be shaded boldly

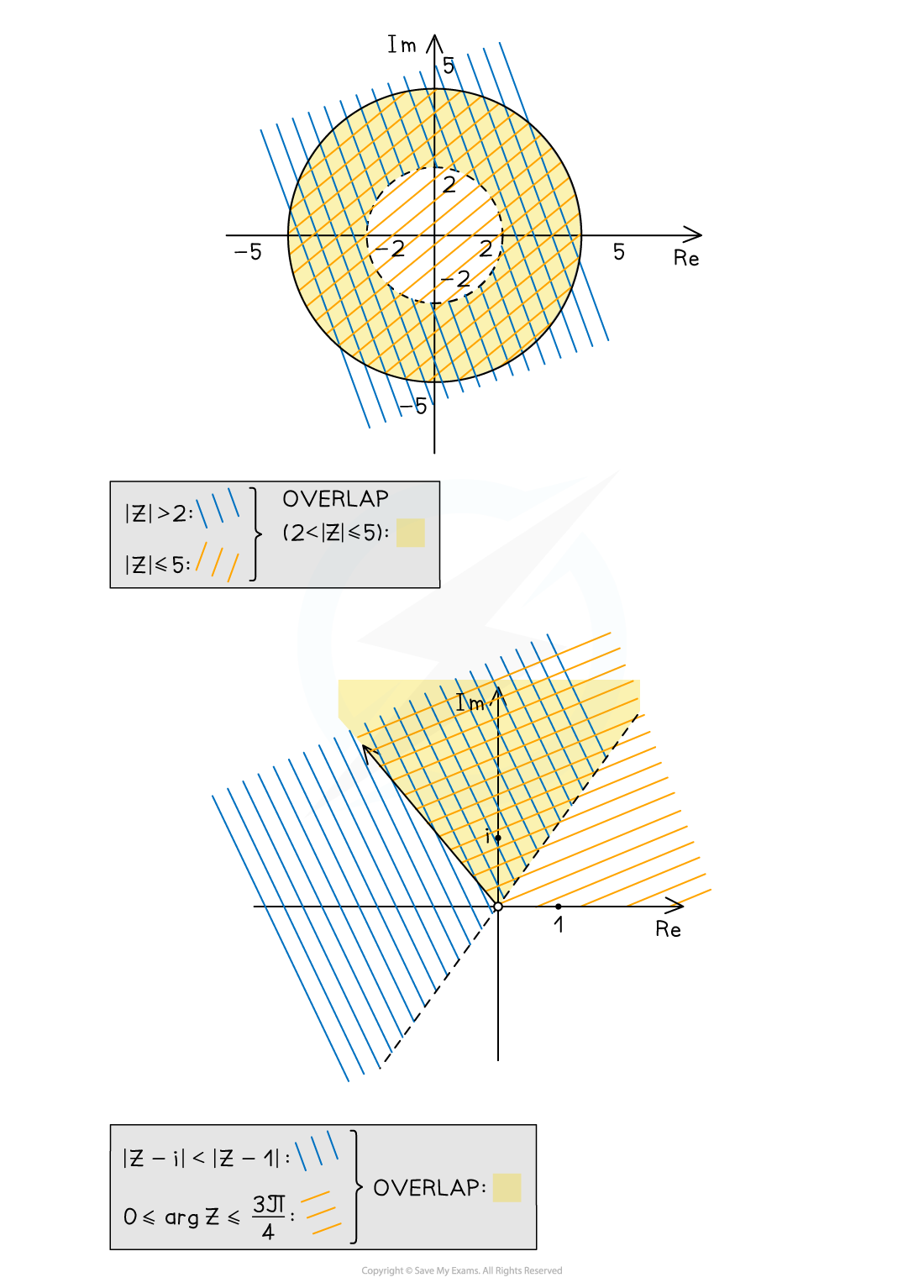
The inequalities $2 < | z | \leq 5$ on the left, the inequalities $| z - i | < | z - 1 |$ and $0 \leq \arg z < \frac{3 π}{4}$ on the right

How do I find the greatest (or least) values of $| z |$ or $\arg z$ in a region?

Every complex number, $z$ , that lies within a region on an Argand diagram will have its own modulus, $|z|$ , that is measured from the origin
For any shaped region…
- The least value of $| z |$ is the distance from the origin to the nearest point in the region
- The greatest value of $| z |$ is the distance from the origin to the farthest point in the region
- Sometimes the least value is zero (if the origin is in the region) and/or the greatest value is infinite (if the region is unbounded)
For circular regions that do not contain the origin…
- Find the length from the origin to the centre of the circle…
- then add a radius for the greatest value of $| z |$ or subtract a radius for the least value of $| z |$
Every complex number, $z$ , that lies within a region on an Argand diagram will have its own argument, $\arg z$ , as measured from the origin
For any shaped region…
- The least value of is $\arg z$ the smallest angle a line through the origin can make to a point in the region
- The greatest value of $\arg z$ is the largest angle a line through the origin can make to a point in the region
For circular regions that do not contain the origin…
- Find $θ$ , the argument of the centre…
- Find $α$ , the angle between a tangent to the circle through the origin and the line from the origin to the centre…
  - This can be done using trigonometry, as a radius meets a tangent at right angles
- The greatest value of $\arg z$ is $θ + α$ and the least value of $\arg z$ is $θ - α$

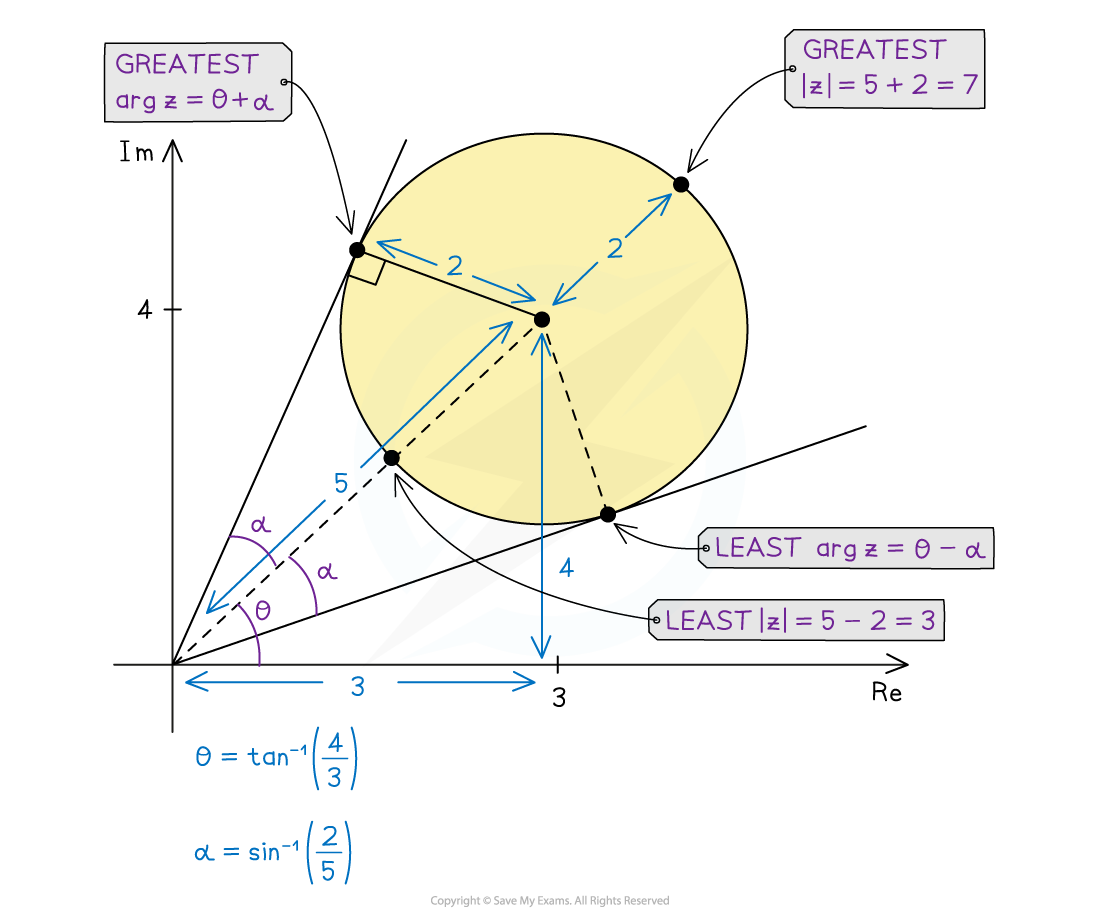
8-2-5_notes_fig6

Find greatest and least values of $|z|$ and $\arg z$

Worked example

ru-S_Kow_8-2-5_example_fig1-part-1

3T~_4SUb_8-2-5_example_fig1-part-2

oa5Q2N4J_8-2-5_example_fig1-part-3

Examiner Tip

When shading an unbounded region in the exam, make sure you extend your shading outwards, crossing any axes where necessary.
When shading multiple inequalities to find a common region, lots of methods are accepted; these include lightly shading individual regions to see where they overlap, or starting to shade along the boundaries of individual regions to find the common region, or marking individual regions to find the region with multiple marks, etc.

Inequalities & Regions in Argand Diagrams (CIE A Level Maths: Pure 3)

Revision Note