Geometry of Complex Addition, Subtraction & Conjugation

What does addition look like on an Argand diagram?

The addition of complex numbers can be shown by the addition of corresponding column vectors
- If $z_{1} = a + b i$ and $z_{2} = c + d i$ , then $z_{1} + z_{2} = (a + b i) + (c + d i)$
- This can be written as

$(\binom{a}{b}) + (\binom{c}{d}) = (\binom{a + c}{b + d})$

- An alternative is to write $(a + b i) + (c + d i)$ as $(a + c) + (b + d) i$ , adding the respective real and imaginary parts separately

A complex number $x + y i$ can be represented by the position vector $(\binom{x}{y})$

What does subtraction look like on an Argand diagram?

As with addition we can use knowledge of vectors to represent subtraction of complex numbers
- If $z_{1} = a + b i$ and $z_{2} = c + d i$ , then $z_{1} - z_{2} = (a + b i) - (c + d i)$
- This can be written as

$(\binom{a}{b}) - (\binom{c}{d}) = (\binom{a - c}{b - d})$

- An alternative is to write $(a + b i) - (c + d i)$ as $(a - c) + (b - d) i$ , subtracting the respective real and imaginary parts separately

What are the geometric representations of complex addition and subtraction?

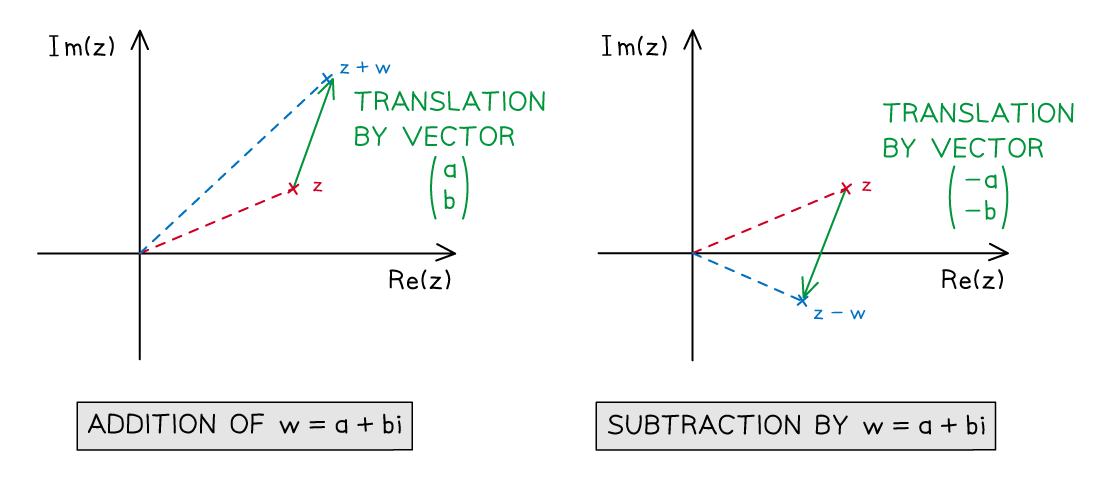
Let w be a given complex number with real part a and imaginary part b
- $w = a + b i$
Let z be any complex number represented on an Argand diagram
Adding w to z results in z being translated by vector $(\begin{matrix} a \\ b \end{matrix})$
Subtracting w from z results in z being translated by vector $(\begin{matrix} - a \\ - b \end{matrix})$

8-2-2-geometry-of-complex-diagram-1

What is the geometric representation of complex conjugation?

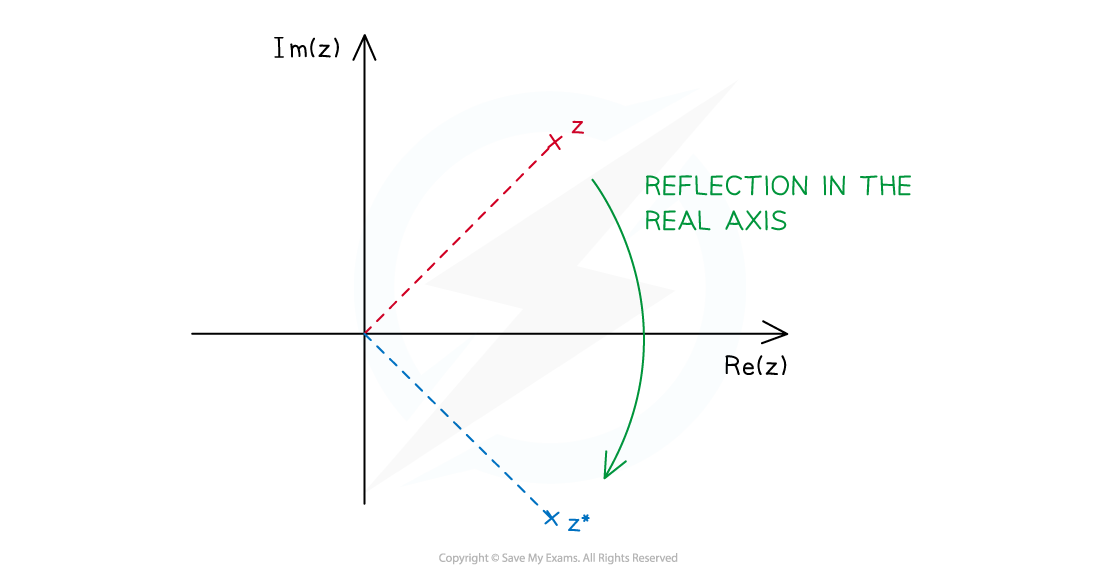
If we plot complex conjugate pairs on an Argand diagram, we notice the points are reflections of each other in the real axis
Let z be any complex number represented on an Argand diagram
Complex conjugating z results in z being reflected in the real axis

8-2-2-geometry-of-complex-diagram-2

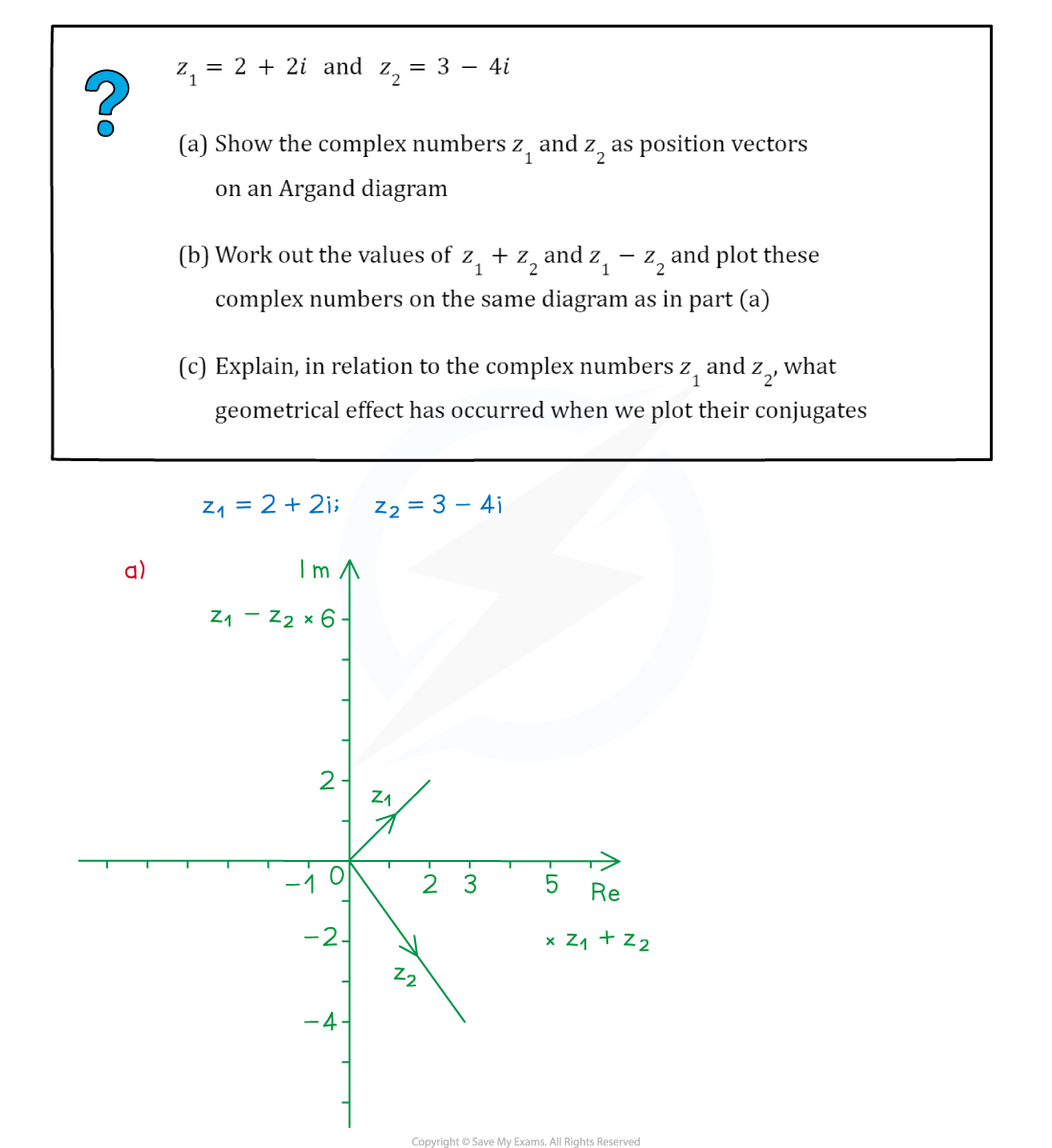
Worked example

8-2-2-geometry-of-complex-addition-subtraction-_-conjugation-example-solution-part-1

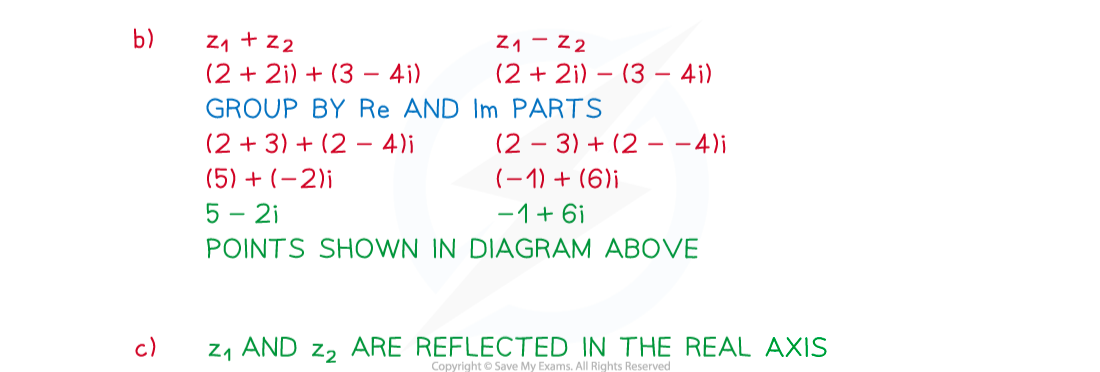
8-2-2-geometry-of-complex-addition-subtraction-and-conjugation-example-solution-part-2

Examiner Tip

Read questions carefully; is it asking to plot the complex number as a point or as a vector?

Be extra careful when representing subtraction geometrically, remember that the solution will be a translation of the shorter diagonal of the parallelogram made up by the two vectors.

Geometry of Complex Addition, Subtraction & Conjugation (CIE A Level Maths: Pure 3)

Revision Note