Uses of the Scalar Product

This revision note covers several applications of the scalar product for vectors – namely, how you can use the scalar product to:

find the angle between vectors or lines
test whether vectors or lines are perpendicular
find the closest distance from a point to a line

How do I find the angle between two vectors?

Recall that a formula for the scalar (or ‘dot’) between vectors $a$ and $b$ is

$a \cdot b = |a| |b| \cos θ$

- where $θ$ is the angle between the vectors when they are placed ‘base to base’
  - that is, when the vectors are positioned so that they start at the same point
- We arrange this formula to make $\cos θ$ the subject:
- To find the angle between two vectors
  - Calculate the scalar product between them
  - Calculate the magnitude of each vector
  - Use the formula to find $\cos θ$
  - Use inverse trig to find $θ$

How do I find the angle between two lines?

To find the angle between two lines, find the angle between their direction vectors

- For example, if the lines have equations $r = a_{1} + s d_{1}$ and $r = a_{2} + t d_{2}$ , then the angle $θ$ between the lines is given by

$θ = \cos^{- 1} (\frac{d_{1} \cdot d_{2}}{|d_{1}| |d_{2}|})$

How do I tell if vectors or lines are perpendicular?

Two (non-zero) vectors $a$ and $b$ are perpendicular if, and only if, $a \cdot b = 0$
- If the a and b are perpendicular then:
  - $θ = 90 ° \Rightarrow \cos θ = 0 \Rightarrow |a| |b| \cos θ = 0 \Rightarrow a \cdot b = 0$
- If $a \cdot b = 0$ then:
  - $|a| |b| \cos θ = 0 \Rightarrow \cos θ = 0 \Rightarrow θ = 90 ° \Rightarrow$ a and b are perpendicular
- For example, the vectors $2 i - 3 j + 5 k$ and $- 4 i - j + k$ are perpendicular since

$(2 i - 3 j + 5 k) \cdot (- 4 i - j + k) = 2 \times (- 4) + (- 3) \times (- 1) + 5 \times 1 = - 8 + 3 + 5 = 0$

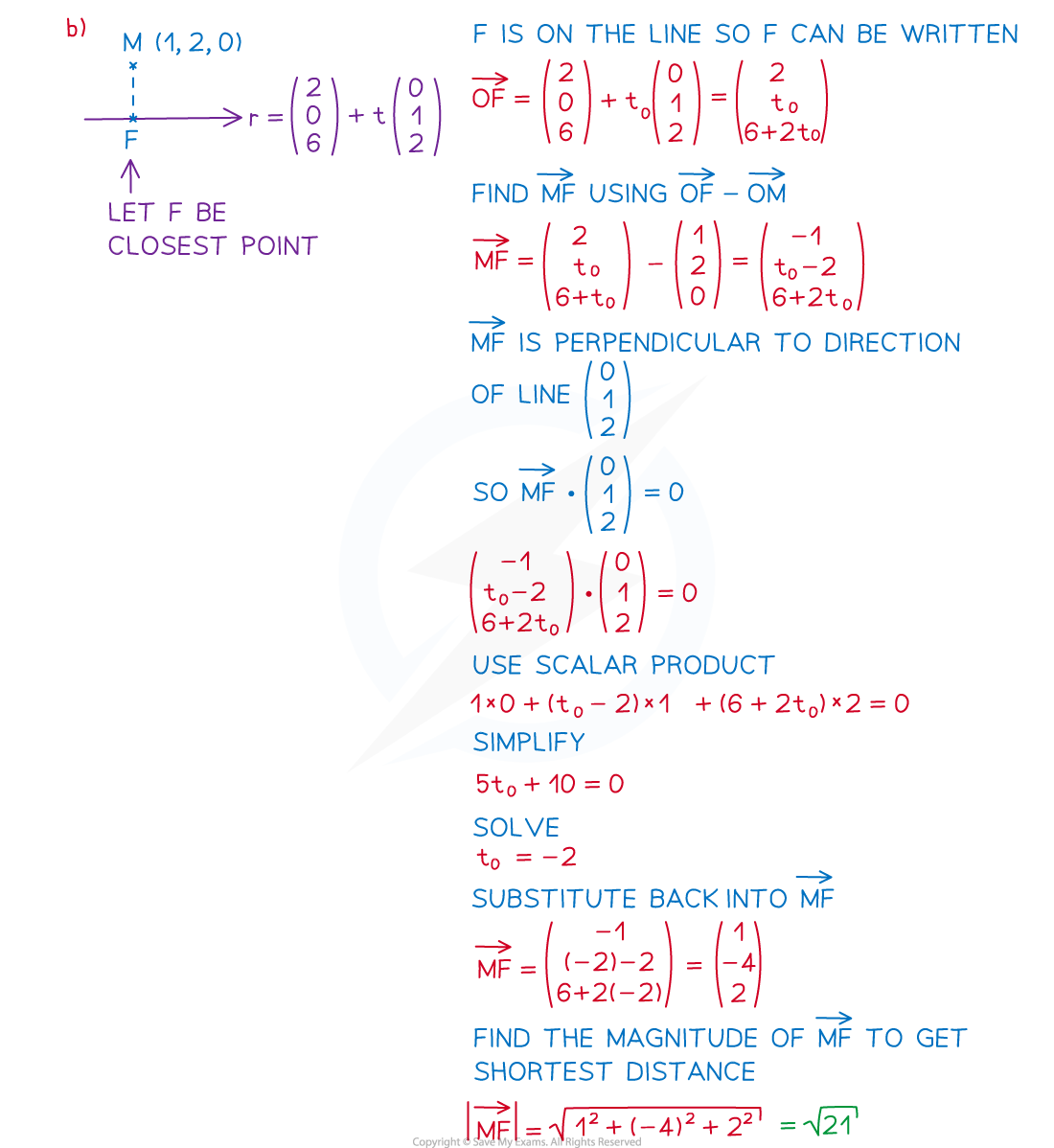
How do I find the shortest distance from a point to a line?

Suppose that we have a line $l$ with equation $r = a + t d$ and a point $P$ not on $l$
Let $F$ be the point on $l$ which is closest to $P$ (sometimes called the foot of the perpendicular)
- Then the line between $F$ and $P$ will be perpendicular to the line $l$
To find the closest point $F$
- Call $f = \vec{OF}$ and $p = \vec{O P}$
- Since $F$ lies on $l$ , we have $f = a + t_{0} d$ , for a unique real number $t_{0}$
- Find the vector $\vec{F P}$ using $p - f$
- $\vec{F P}$ is perpendicular to $d$ so form an equation using $(p - f) \cdot d = 0$
- Solve this equation to find the value of $t_{0}$
- Use the value of $t_{0}$ to find $f$
The shortest distance between the point and the line is the length
Note that the shortest distance between the point and the line is sometimes referred to as the length of the perpendicular

Worked example

7-3-4-uses-of-scalar-product-we-solution-part-1

7-3-4-uses-of-scalar-product-we-solution-part-2

Examiner Tip

It can be easier and clearer to work with column vectors when dealing with scalar products.

Uses of the Scalar Product (CIE A Level Maths: Pure 3)

Revision Note

How do I find the angle between two vectors?

How do I find the angle between two lines?

How do I tell if vectors or lines are perpendicular?

How do I find the shortest distance from a point to a line?

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

1. Algebra & Functions

1.1 Modulus Functions

1.1.1 Modulus Functions - Sketching Graphs

1.1.2 Modulus Functions - Solving Equations

1.2 Polynomials

1.2.1 Polynomial Division

1.2.2 Factor & Remainder Theorem

1.2.3 Factorisation

1.2.4 Rational Expressions

1.2.5 Top Heavy Rational Expressions

1.3 Partial Fractions

1.3.1 Linear Denominators

1.3.2 Squared Linear Denominators

1.3.3 Quadratic Denominators

1.4 Further Modelling with Functions

1.4.1 Further Modelling with Functions

1.5 General Binomial Expansion

1.5.1 General Binomial Expansion

1.5.2 General Binomial Expansion - Subtleties

1.5.3 General Binomial Expansion - Multiple

1.5.4 Approximating values

2. Logs & Exponentials

2.1 Logarithmic & Exponential Function

2.1.1 Exponential Functions

2.1.2 Logarithmic Functions

2.1.3 "e"

2.1.4 Derivatives of Exponential Functions

2.2 Laws of Logarithms

2.2.1 Laws of Logarithms

2.2.2 Exponential Equations

2.3 Modelling with Logs & Exponentials

2.3.1 Exponential Growth & Decay

2.3.2 Using Exps & Logs in Modelling

2.3.3 Using Log Graphs in Modelling

3. Trigonometry

3.1 Reciprocal Trigonometric Functions

3.1.1 Reciprocal Trig Functions - Definitions

3.1.2 Reciprocal Trig Functions - Graphs

3.1.3 Trigonometry - Further Identities

3.2 Compound & Double Angle Formulae

3.2.1 Compound Angle Formulae

3.2.2 Double Angle Formulae

3.2.3 R addition formulae Rcos Rsin etc

3.3 Further Trigonometric Equations

3.3.1 Strategy for Further Trigonometric Equations

3.4 Trigonometric Proof

3.4.1 Trigonometric Proof

4. Differentiation

4.1 Further Differentiation

4.1.1 Differentiating Other Functions (Trig, ln & e etc)

4.1.2 Product Rule

4.1.3 Quotient Rule

4.2 Implicit Differentiation

4.2.1 Implicit Differentiation

4.3 Differentiation of Parametric Equations

4.3.1 Parametric Equations - Basics

4.3.2 Parametric Equations - Eliminating the Parameter

4.3.3 Parametric Equations - Sketching Graphs

4.3.4 Parametric Differentiation

5. Integration

5.1 Further Integration

5.1.1 Integrating Other Functions (Trig, ln & e etc)

5.1.2 Integrating with Trigonometric Identities

5.1.3 f'(x)/f(x)

5.1.4 Substitution (Reverse Chain Rule)

5.1.5 Harder Substitution

5.1.6 Integration by Parts

5.1.7 Integration using Partial Fractions

5.1.8 Integration Decision Making

5.2 Differential Equations

5.2.1 General Solutions