A LevelMaths: Pure 3CIERevision Notes4. Differentiation4.1 Further Differentiation4.1.1 Differentiating Other Functions (Trig, ln & e etc)

Differentiating Other Functions (Trig, ln & e etc) (CIE A Level Maths: Pure 3)

Revision Note

Lucy

Author

Last updated

4 August 2023

Did this video help you?

Differentiating Other Functions (Trig, ln & e etc)

How do I differentiate common functions?

These are the common results
- $\frac{d}{d x} (x^{n}) = n x^{n - 1}$
- $\frac{d}{d x} (e^{x}) = e^{x}$
- $\frac{d}{d x} (a^{x}) = a^{x} \ln a$ for $a > 0$
- $\frac{d}{d x} (\ln x) = \frac{1}{x}$
- $\frac{d}{d x} (\sin x) = \cos x$
- $\frac{d}{d x} (\cos x) = - \sin x$
- $\frac{d}{d x} (\tan x) = \sec^{2} x$
- $\frac{d}{d x} (\cot x) = - \cos {ec}^{2} x$
- $\frac{d}{d x} (\sec x) = \sec x \tan x$
- $\frac{d}{d x} (\cos ec x) = - \cos ec x \cot x$
- $\frac{d}{dx} (\tan^{- 1} x) = \frac{1}{1 + x^{2}}$

How do I differentiate exponentials and logarithms?

The two basic differentiation formulae are:

Diff Other Funct Illustr 1, AS & A Level Maths revision notes

From those basic formulae are derived these two additional formulae:

Diff Other Funct Illustr 2_forms, AS & A Level Maths revision notes

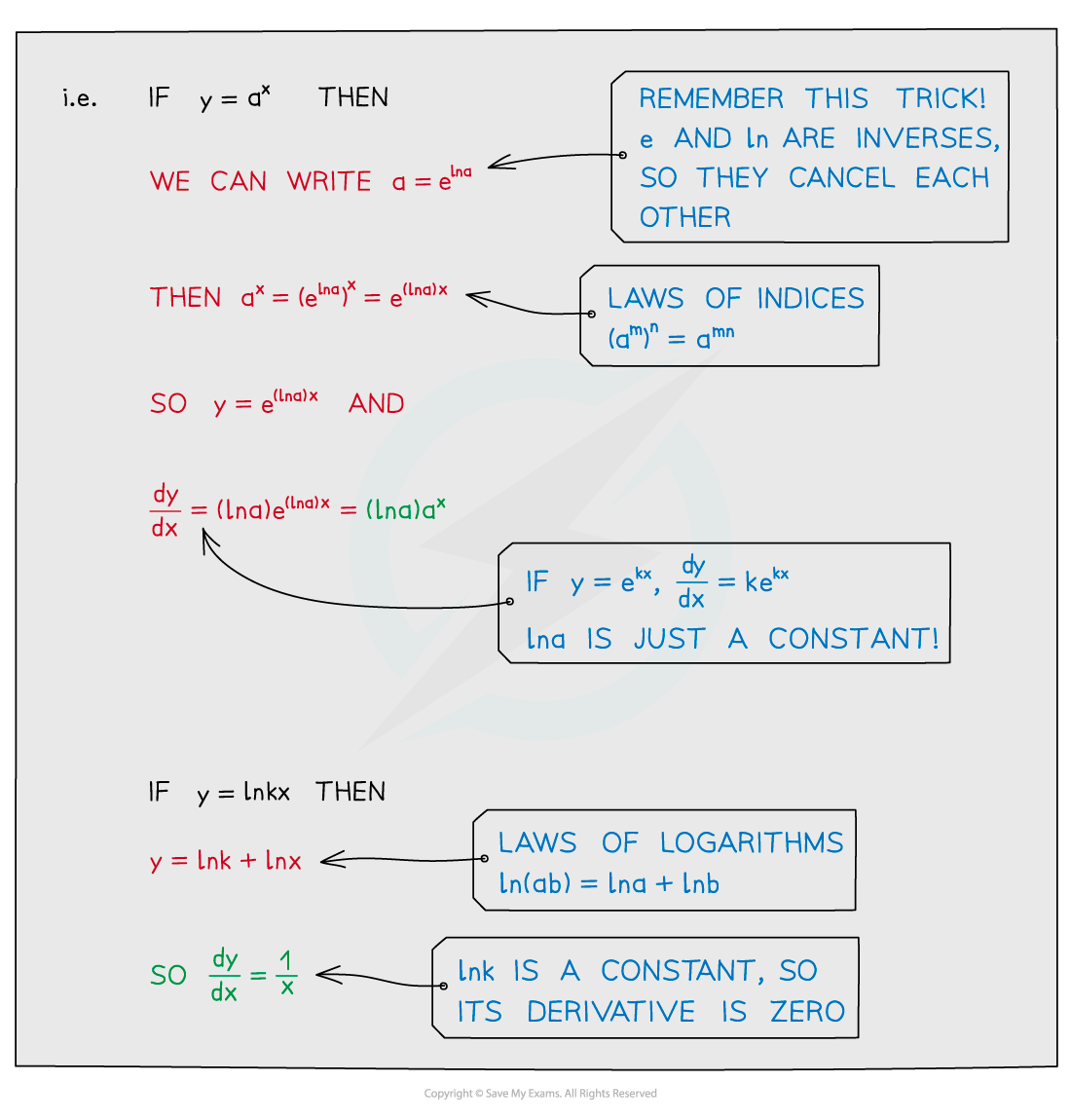
Diff Other Funct Illustr 2_derivs, AS & A Level Maths revision notes

And for exponentials more generally:

Diff Other Funct Illustr 3, AS & A Level Maths revision notes

This last formula can be derived from Formula 3 by using the chain rule

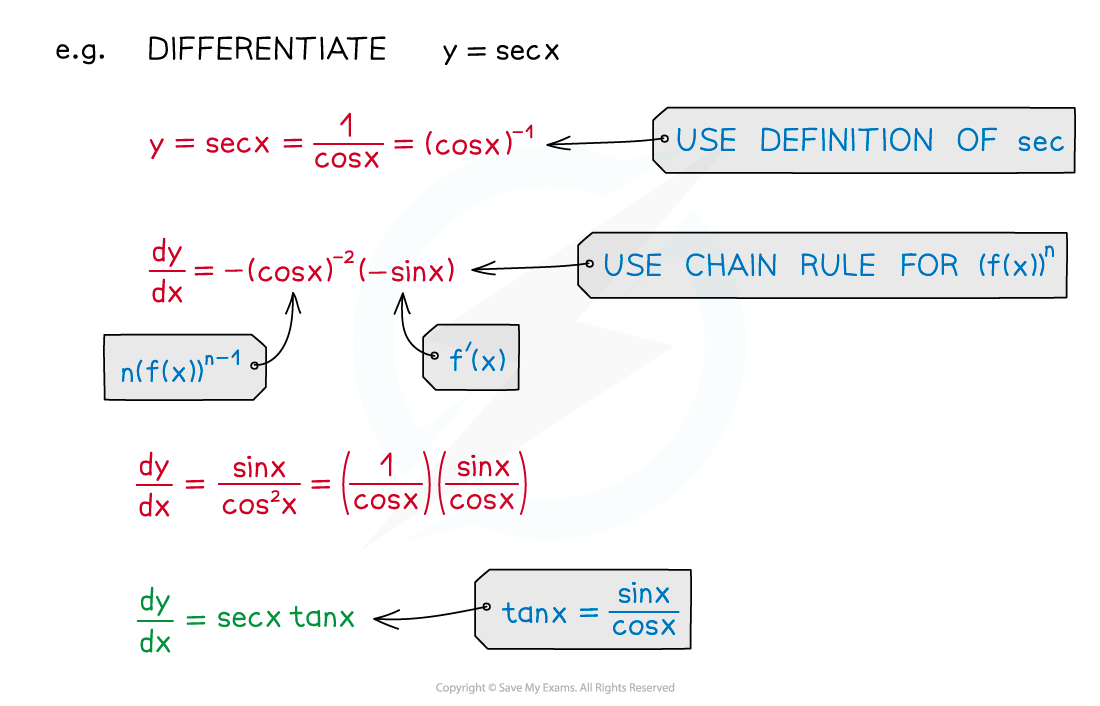
How do I differentiate the reciprocal trigonometric functions?

The formulae for the derivatives of the reciprocal trigonometric functions are:

\frac{d}{d x} (\sec x) = \sec x \tan x

\frac{d}{d x} (cosec x) = - cosec x \cot x

\frac{d}{d x} (\cot x) = - {cosec}^{2} x

You can derive the derivatives for sec, cosec, and cot using the chain rule and the derivatives of the basic trigonometric functions

Diff Rec Inv Trig Illustr 1, AS & A Level Maths revision notes

Examiner Tip

All of the above are in the formula book, make sure you know how to find them.
They will be particularly useful when working with identities and when integrating trigonometric functions.
Recognising the derivative of tan^-1x will be particularly useful for integrating some functions.

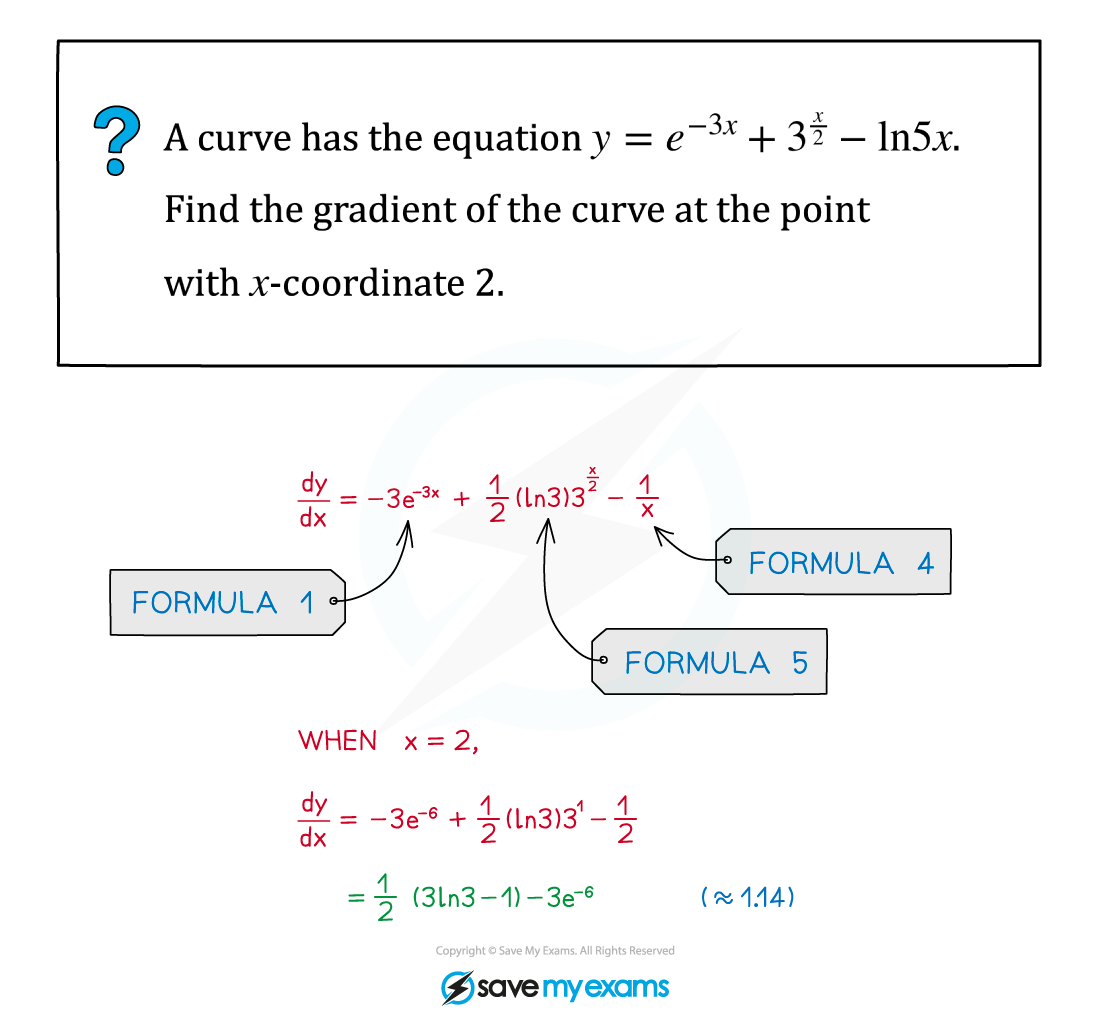
Worked example

Diff Other Funct Example, AS & A Level Maths revision notes

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself Next topic

Did this page help you?

More Exam Questions you might like

Lucy

Author: Lucy

Expertise: Head of STEM

Lucy has been a passionate Maths teacher for over 12 years, teaching maths across the UK and abroad helping to engage, interest and develop confidence in the subject at all levels. Working as a Head of Department and then Director of Maths, Lucy has advised schools and academy trusts in both Scotland and the East Midlands, where her role was to support and coach teachers to improve Maths teaching for all. Lucy has created revision content for a variety of domestic and international Exam Boards including Edexcel, AQA, OCR, CIE and IB.