Revision NotesExam QuestionsPast PapersMock Exams
A LevelMathsCambridge (CIE)Pure 3Revision NotesTrigonometryReciprocal Trigonometric FunctionsIdentities with Reciprocal Trigonometric Functions

Identities with Reciprocal Trigonometric Functions (Cambridge (CIE) A Level Maths): Revision Note

Exam code: 9709

Roger B

Author

Roger B

Last updated

Cambridge (CIE) Maths: Pure 3OCR Maths A: PureAQA Maths: PureEdexcel Maths: Pure

Identities with reciprocal trigonometric functions

What are the reciprocal trigonometric identities?

  • There are two identities with sec, cosec and cot that you need to know and be able to use:

    • tan2x + 1 ≡ sec2x

    • 1 + cot2x ≡ cosec2x

  • These are not really 'new' identities – they can both be derived from sin2x + cos2x ≡ 1

    • To derive the identity for sec2x  divide  sin2x + cos2x ≡ 1  by cos2x

    • To derive the identity for cosec2x  divide  sin2x + cos2x ≡ 1  by sin2x

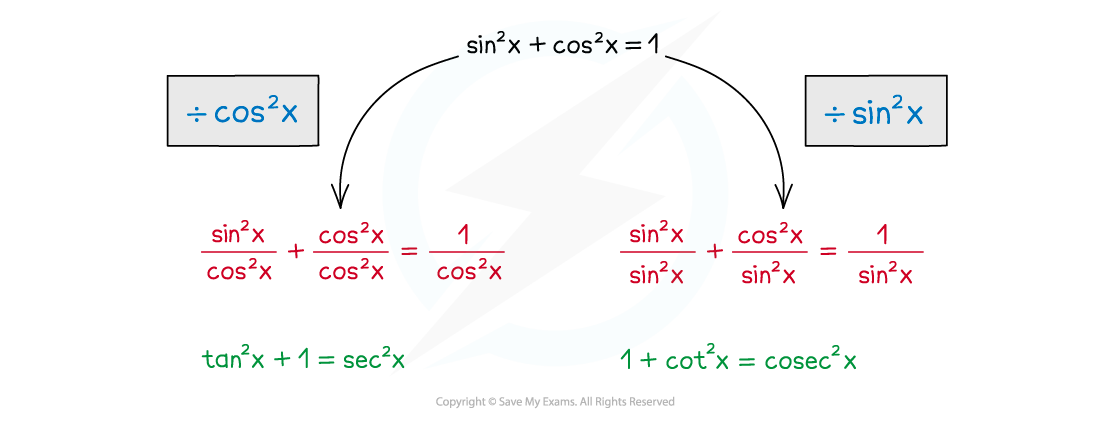
Trig Fur IDs Illustr 1, A Level & AS Maths: Pure revision notes

Examiner Tips and Tricks

  • These identities are not given in the exam formulae booklet – make sure you know how to find them. 

  • They will be needed to prove some trigonometric identities and solve some trigonometric equations.

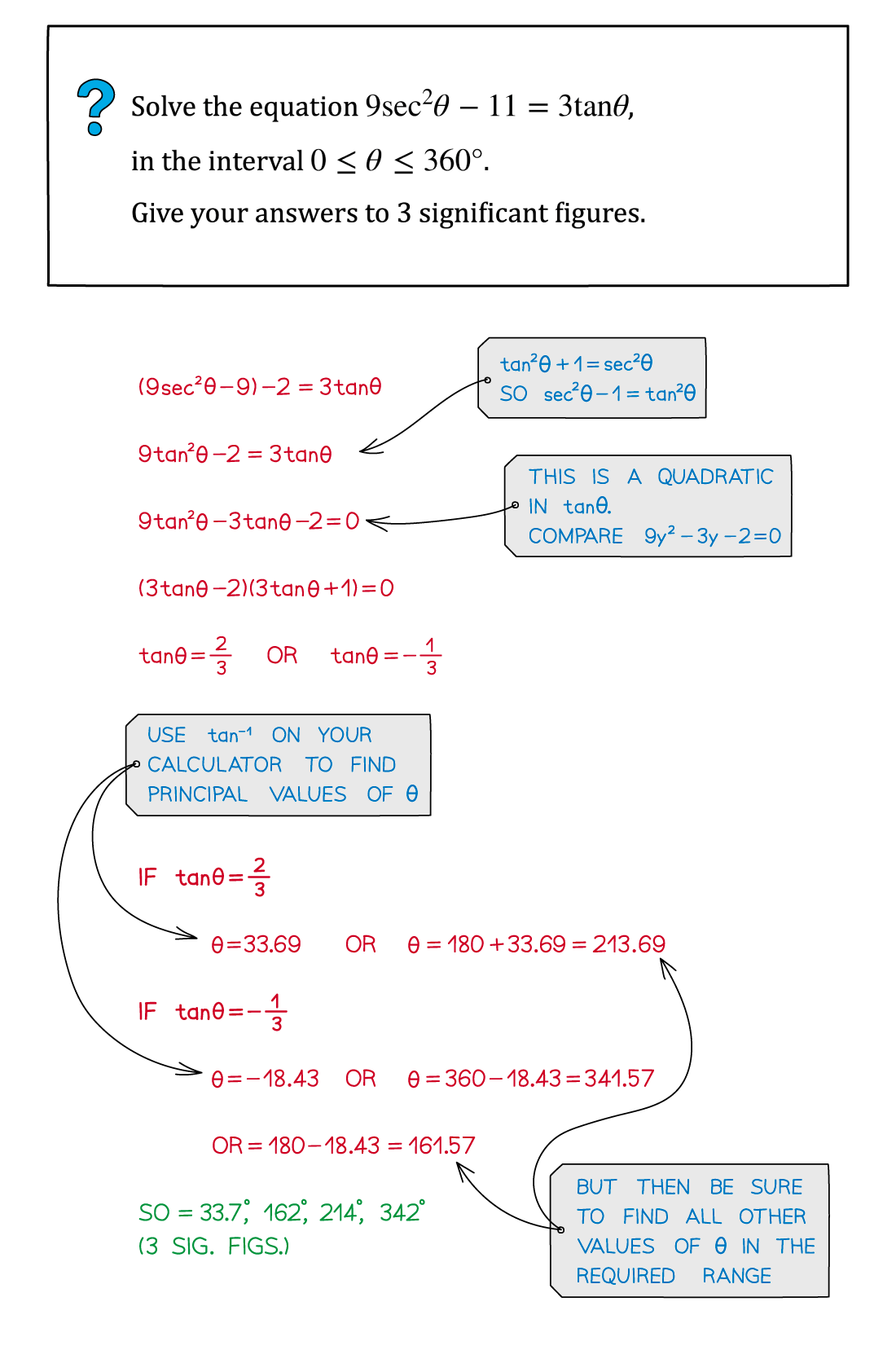
Worked Example

Trig Fur IDs Example, A Level & AS Maths: Pure revision notes
For teachers

Ready to test your students on this topic?

  • Create exam-aligned tests in minutes
  • Differentiate easily with tiered difficulty
  • Trusted for all assessment types
Explore Test Builder
Test Builder in a diagram showing questions being picked from different difficulties and topics, and being downloaded as a shareable format.
Test yourself
Previous:Graphs of Reciprocal Trigonometric FunctionsNext:Compound Angle Formulae
Roger B

Author: Roger B

Expertise: Maths Content Creator

Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.