Polynomial Division (Cambridge (CIE) A Level Maths): Revision Note
Exam code: 9709
Did this video help you?
Polynomial division
What is a polynomial?
A polynomial is an algebraic expression consisting of a finite number of terms, with non-negative integer indices only
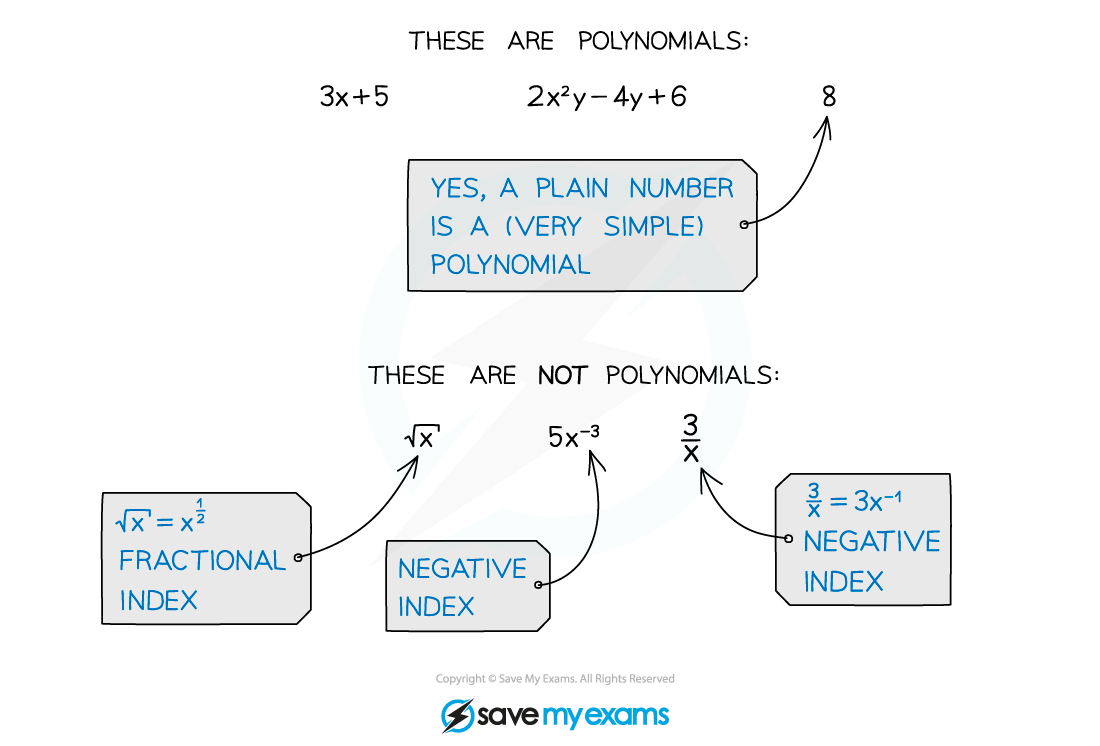
What is polynomial division?
Polynomial division is a method for splitting polynomials into factor pairs (with or without an accompanying remainder term)

At A level you will most frequently use it to factorise polynomials, or when dealing with improper (ie 'top-heavy') algebraic fractions
How do I divide polynomials?
The method used for polynomial division is just like the long division method (sometimes called 'bus stop division') used to divide regular numbers:

At A level you will normally be dividing a polynomial dividend of degree 3 or 4 by a divisor in the form (x ± p)
The answer to a polynomial division question is built up term by term, working downwards in powers of the variable (usually x)
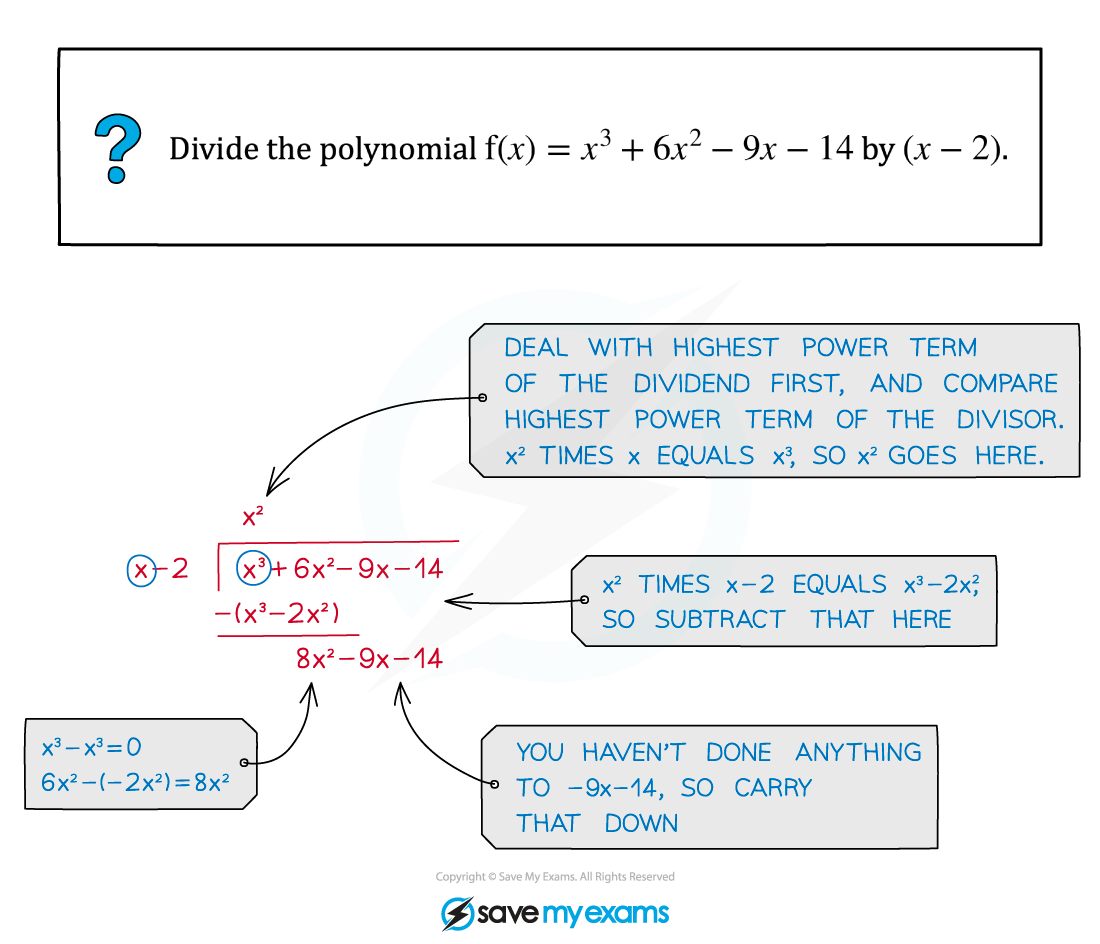
Start by dividing by the highest power term
Write out this multiplied by the divisor and subtract
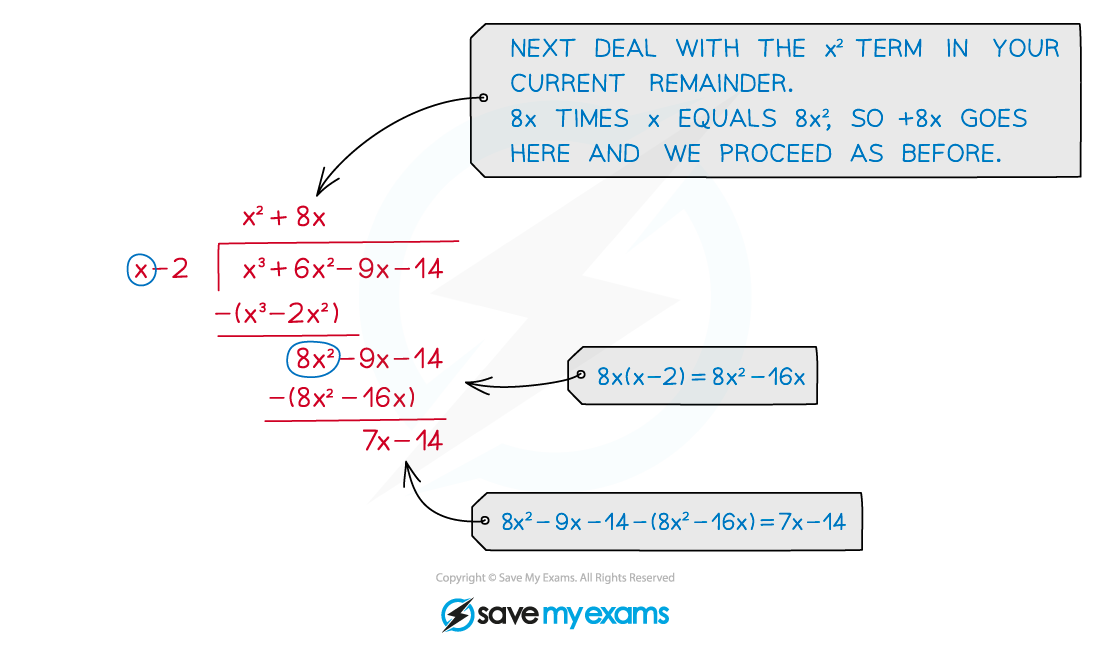
Continue to divide by each reducing power term and subtracting your answer each time
Continue until you are left with zero
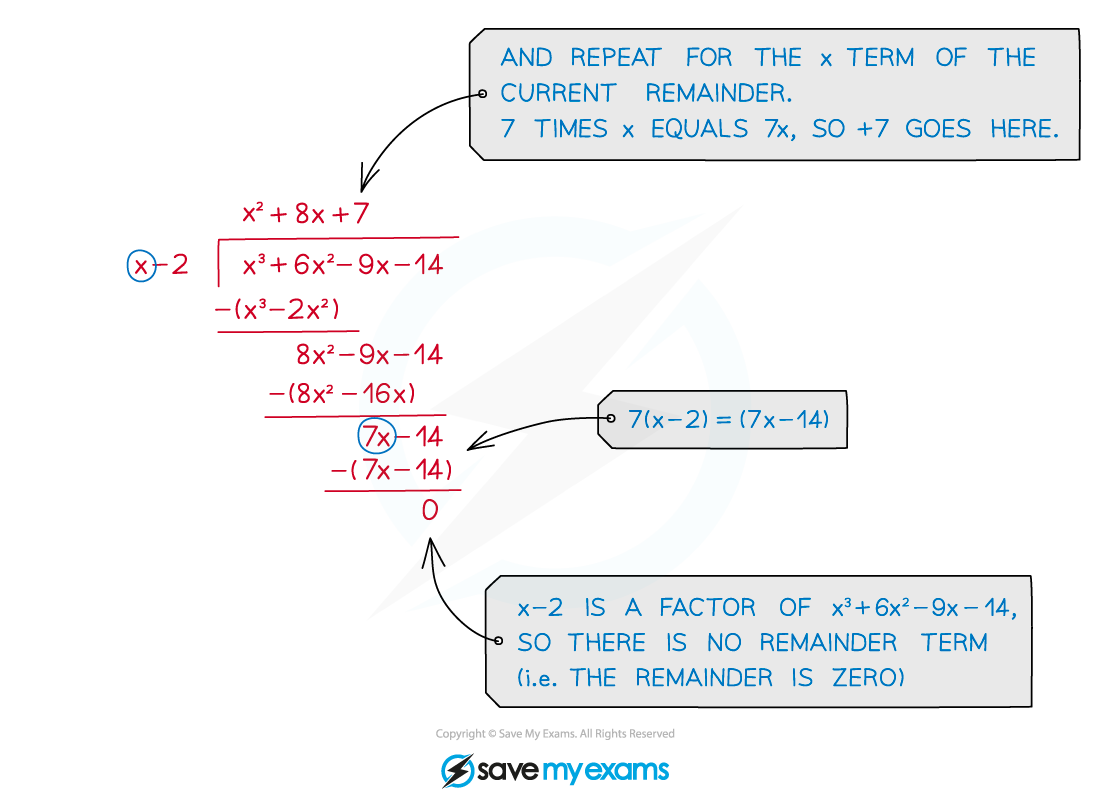
If the divisor is not a factor of the polynomial then there will be a remainder term left at the end of the division
Worked Example
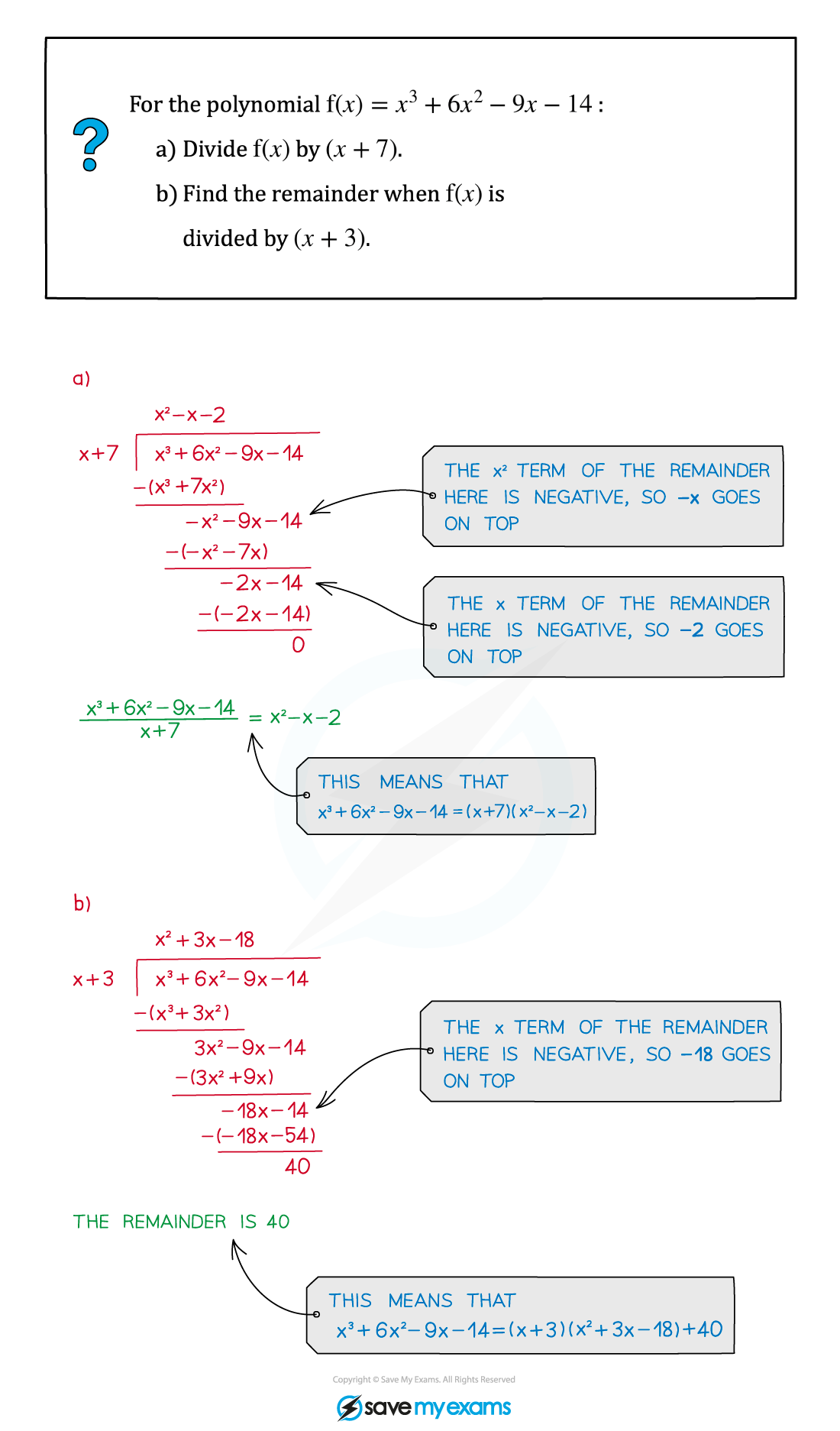
Did this video help you?
Quadratic divisor
What is a quadratic divisor?
Suppose a polynomial of degree
is divided by a quadratic divisor
The quotient q will have degree
The degree of the remainder r will be less than
It could be degree 1 (linear)
Or it could be degree 0 (constant)
How do I divide a polynomial by a quadratic divisor?
You use polynomial division!
Step 1
Divide the leading term of the polynomial by the squared term of the divisorThis gives the leading term of the quotient
Step 2
Multiply this term by the divisorStep 3
Subtract this from the polynomial to get a new polynomial with a lower degreeContinue these steps until you have an expression with a degree lower than 2

Unlock more, it's free!
Did this page help you?