Sketching Reciprocal Graphs (Cambridge (CIE) A Level Maths): Revision Note
Exam code: 9709
Did this video help you?
Sketching reciprocal curves
What are reciprocal graphs?
Reciprocal graphs involve equations with an
term on the denominator e.g.
There are two basic reciprocal graphs to know for A level
and
The second one of these is always positive

More reciprocal graphs
You also need to recognise graphs where the numerator is not one

The sign of a shows which part of the graph the curves are located
The size of a shows how steep the curves are
The closer a is to 0 the more L-shaped the curves are
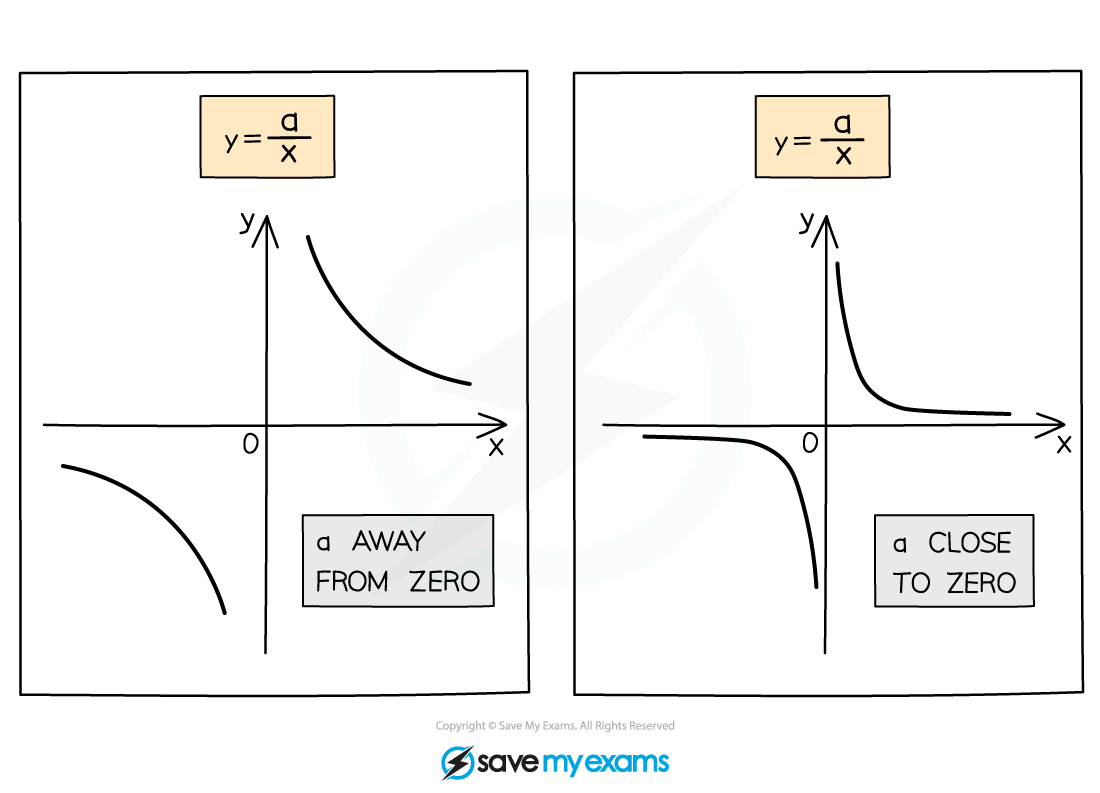
All have two asymptotes
horizontal, y = 0 (x-axis)
vertical, x = 0 (y-axis)
How do I sketch a reciprocal graph?

STEP 1
Use the sign of “a” to locate the curves and use the size of “a” to gauge the steepness of the curveSTEP 2
Sketch the graphSTEP 3
Label the points x = 1 and x = -1 as a guide to the scale of your graphSTEP 4
Draw asymptotes with dotted linesThese graphs do not intercept either axis
Graph transformations of them could cross the axes (see Translations)
Worked Example


Unlock more, it's free!
Was this revision note helpful?
