Modelling with Volumes of Revolution

Many every day objects such as buckets, beakers, vases and lamp shades can be modelled as a solid of revolution
This can then be used to find the volume of the solid (volume of revolution) and/or other information about the solid that could be useful before an object is manufactured
Modelling with volumes of revolution could involve rotation around the x-axis or y-axis so ensure you are familiar with both

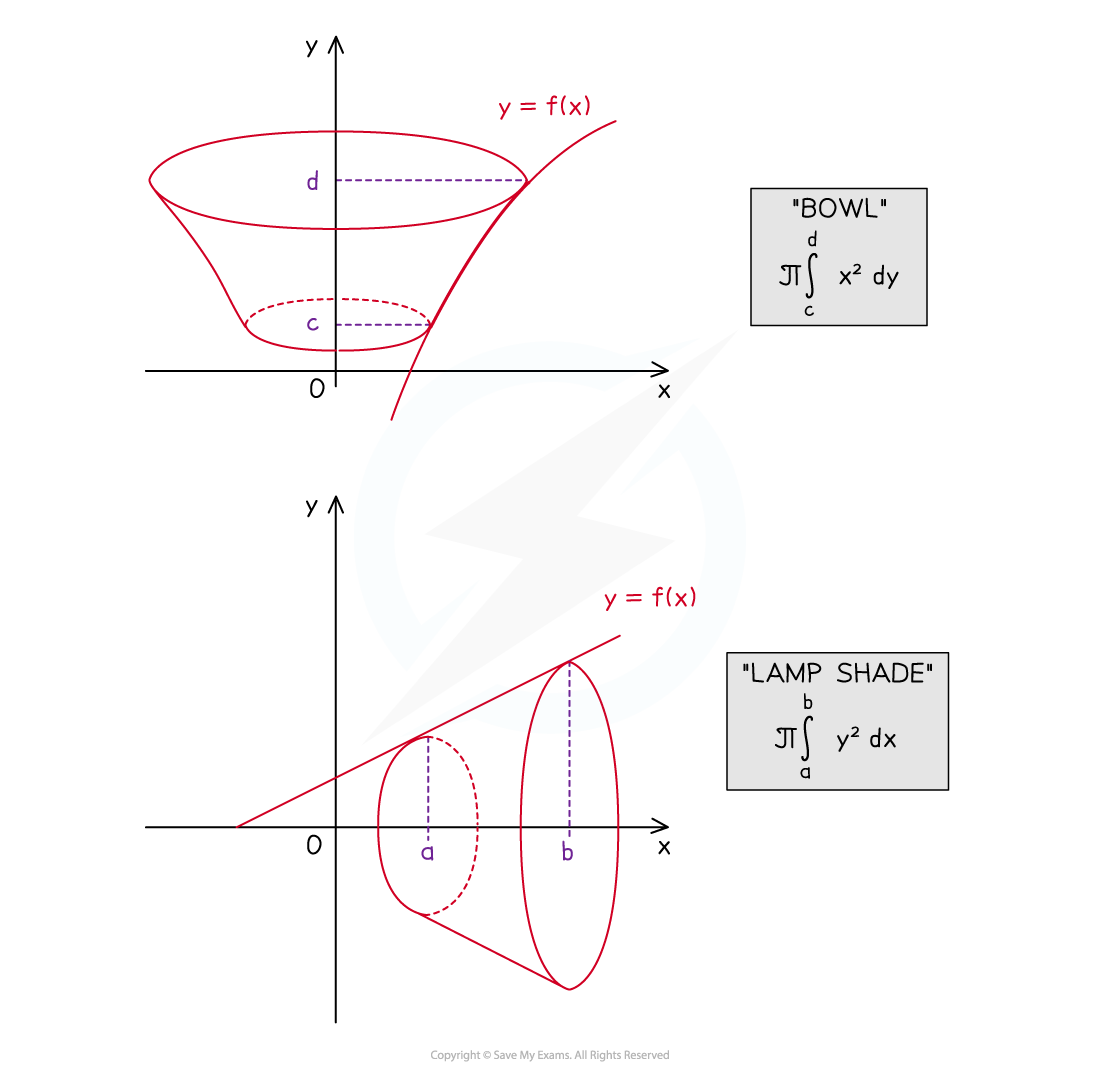
6-2-6-cie-fig1-bowl-and-lamp-1

The solids formed are usually the main shape of the body of the object
- For example, the handles on a vase would not be included
- The lip on the top edge of a bucket would not be considered
A common question or assumption concerns the thickness of a container
- The thickness is generally ignored as it is relatively small compared to the size of the object
  - thickness will depend on the purpose of the object and the material it is made from
- Some questions may refer to the solid formed being the ‘inside’ of an object or refer to the ‘internal’ dimensions
- If the thickness of the material is significant it would involve two related solids of revolution (Adding & Subtracting Volumes)

Visualising and sketching the solid formed can help with starting problems
Familiarity with applying the volume of revolution formulae for rotations around both the x and y axes

x-axis $V = π \int_{a}^{b} y^{2} d x$

y-axis $V = π \int_{c}^{d} x^{2} d y$

The volume of a solid may involve adding or subtracting different volumes of revolution
- Subtraction would need to be used for solids formed from areas that do not have a boundary with the axis of rotation
Questions may go on to ask related questions in context so do take notice of the context
- A question about a bucket being formed may ask about its capacity
This would be measured in litres so there may also be a mix of units that will need conversion (e.g. 1000cm³ = 1 litre)

6-2-6-cie-fig2-we-solution-part-1

6-2-6-cie-fig2-we-solution-part-2

Consider the context of the question to gauge whether your final answer is realistic
- a vase holding just 0.126 litres of water will not hold many flowers, but the question did state it was a miniature vase
For rotation around the y -axis remember to rearrange $y = f (x)$ into the form $x = g (y)$

Modelling with Volumes of Revolution (CIE A Level Maths: Pure 1)