Revision NotesExam QuestionsPast Papers
A LevelMaths: Pure 1CIERevision Notes2. Coordinate Geometry2.2 Circles2.2.3 Bisection of Chords

Bisection of Chords (CIE A Level Maths: Pure 1)

Revision Note

Roger

Author

Roger

Last updated

Did this video help you?

Bisection of Chords

How can I find the equation of a perpendicular bisector?

  • The perpendicular bisector of a line segment:
    • is perpendicular to the line segment
    • goes through the midpoint of the line segment

 

Perpendicular Bisector, A Level & AS Level Pure Maths Revision Notes

  •  The midpoint and gradient of the line segment between points (x1, y1) and (x2, y2) are given by the formulae

 Midpoint Gradient Forms, A Level & AS Level Pure Maths Revision Notes

  •  The gradient of the perpendicular bisector is therefore

Perp Bisector Gradient, A Level & AS Level Pure Maths Revision Notes

  • The equation of the perpendicular bisector is the equation of the line with that gradient through the line segment's midpoint (see Equation of a Straight Line)

How can I use perpendicular bisectors to find the equation of a circle?

  • A chord of a circle is a straight line segment between any two points on the circle

Chord, A Level & AS Level Pure Maths Revision Notes

  • The perpendicular bisector of a chord always goes through the centre of the circle

Perp Bisect Chord, A Level & AS Level Pure Maths Revision Notes

  • If you know three points on a circle, draw any two chords between them – the perpendicular bisectors of the chords will meet at the centre of the circle

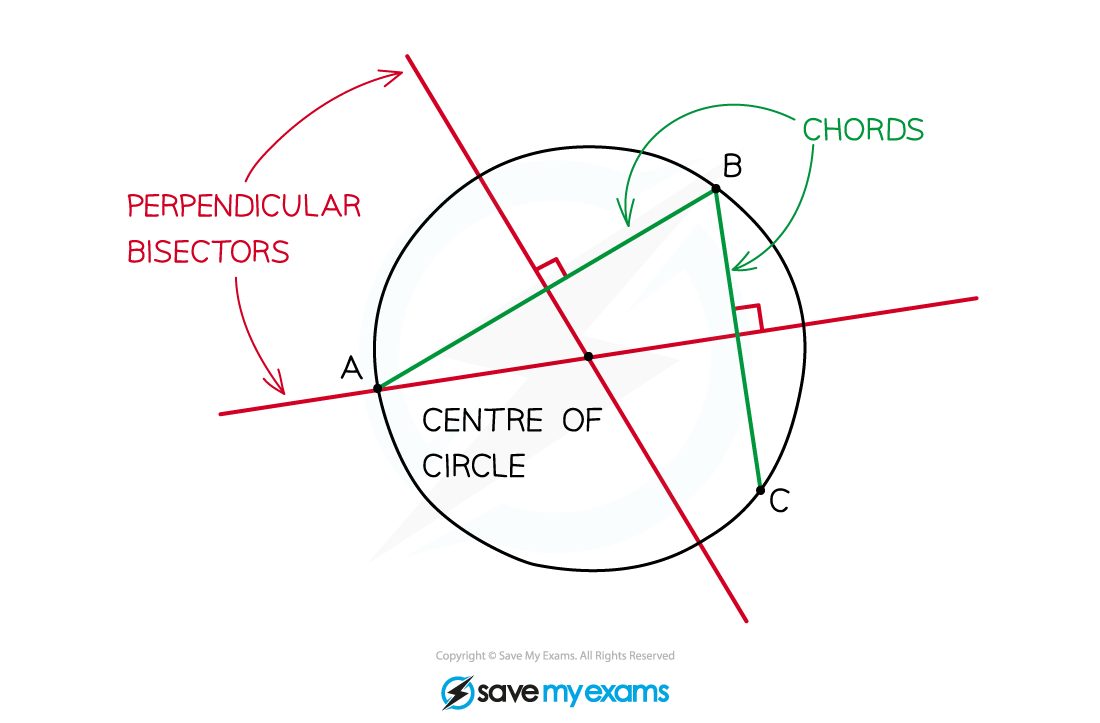
Perp Bisect Centre, A Level & AS Level Pure Maths Revision Notes

  • Now that you know the centre of the circle and a point on the circle you can write the equation of the circle

Examiner Tip

  • To find the point of intersection of two straight lines, set the equations of the lines equal to each other and solve. Find lines intersect, A Level & AS Level Pure Maths Revision Notes

Worked example

Bisect Chords Example, A Level & AS Level Pure Maths Revision Notes

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:2.2.2 Finding the Centre & RadiusNext:2.2.4 Angle in a Semicircle
    Roger

    Author: Roger

    Expertise: Maths

    Roger's teaching experience stretches all the way back to 1992, and in that time he has taught students at all levels between Year 7 and university undergraduate. Having conducted and published postgraduate research into the mathematical theory behind quantum computing, he is more than confident in dealing with mathematics at any level the exam boards might throw at you.