Reciprocal Graphs - Sketching (CIE A Level Maths: Pure 1)

What are reciprocal graphs?

• Reciprocal graphs involve equations with an term on the denominator e.g.
• There are two basic reciprocal graphs to know for A level

  and   

• The second one of these is always positive

More reciprocal graphs

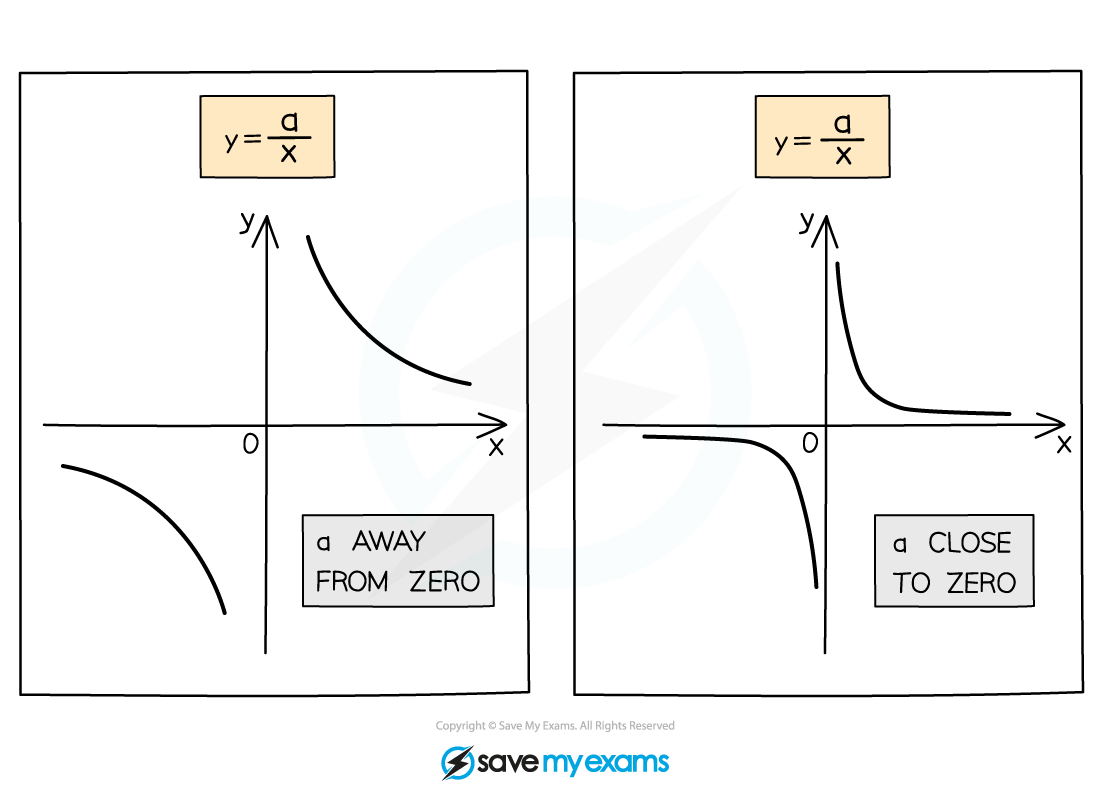
• You also need to recognise graphs where the numerator is not one

• The sign of a shows which part of the graph the curves are located
• The size of a shows how steep the curves are
  • The closer a is to 0 the more L-shaped the curves are

   

• • horizontal, y = 0 (x-axis)
  • vertical, x = 0 (y-axis)All have two asymptotes

How do I sketch a reciprocal graph?

STEP 1        Use the sign of “a” to locate the curves

and use the size of “a” to gauge the steepness of the curve

STEP 2        Sketch the graph

STEP 3        Label the points x = 1 and x = -1 as a guide to the scale of your graph

STEP 4        Draw asymptotes with a dotted line Draw asymptotes with dotted lines

• These graphs do not intercept either axis
• Graph transformations of them could cross the axes (see Translations)