Sketching Polynomials (Cambridge (CIE) A Level Maths): Revision Note
Exam code: 9709
Did this video help you?
Sketching polynomials
How do I sketch the graph of a polynomial?
A polynomial is any finite function with non-negative indices, that could mean a quadratic, cubic, quartic or higher power
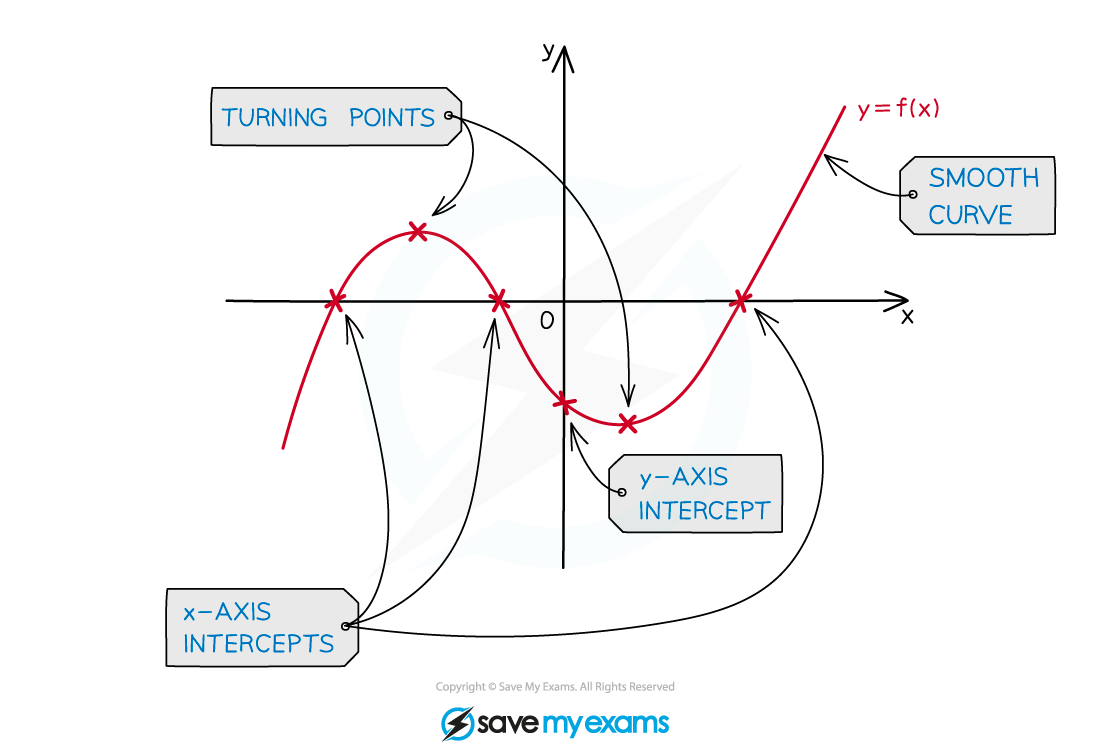
When asked to sketch a polynomial you'll need to think about the following
y-axis intercept
x-axis intercepts (roots)
turning points (maximum and/or minimum)
a smooth curve (this takes practice!)
What steps should I take when sketching a polynomial?
STEP 1 Find the y-axis intercept by setting x = 0
STEP 2 Find the x-axis intercepts (roots) by setting y = 0
STEP 3 Consider the shape and “start”/”end” of the graph
eg. a positive cubic graph starts in third quadrant (“bottom left”) and “ends” in first quadrant (“top right”)
STEP 4 Consider where any turning points should go
STEP 5 Draw with a smooth curve
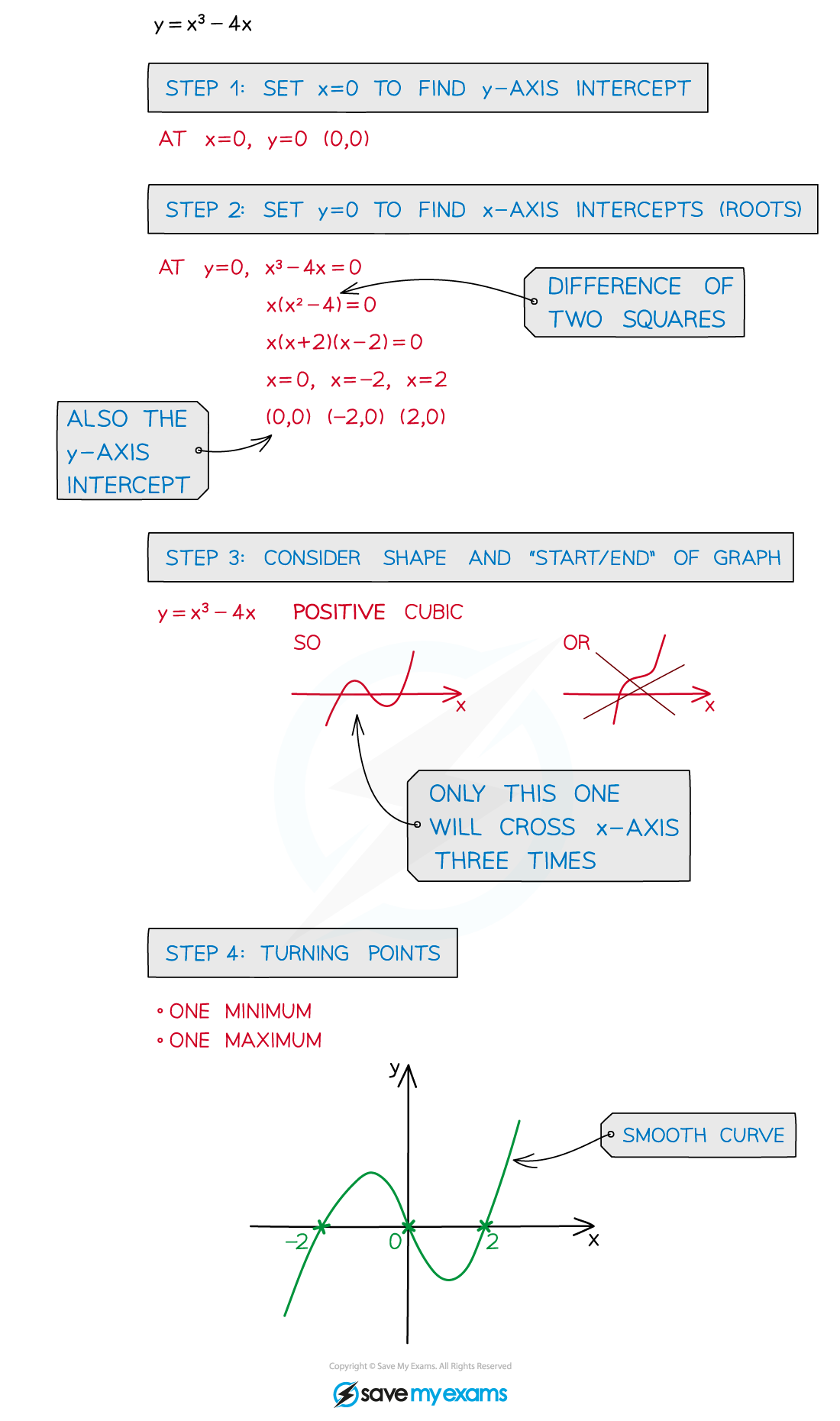

Coordinates of turning points can be found using differentiation
Except with a point of inflection, repeated roots indicate the graph touches the x-axis
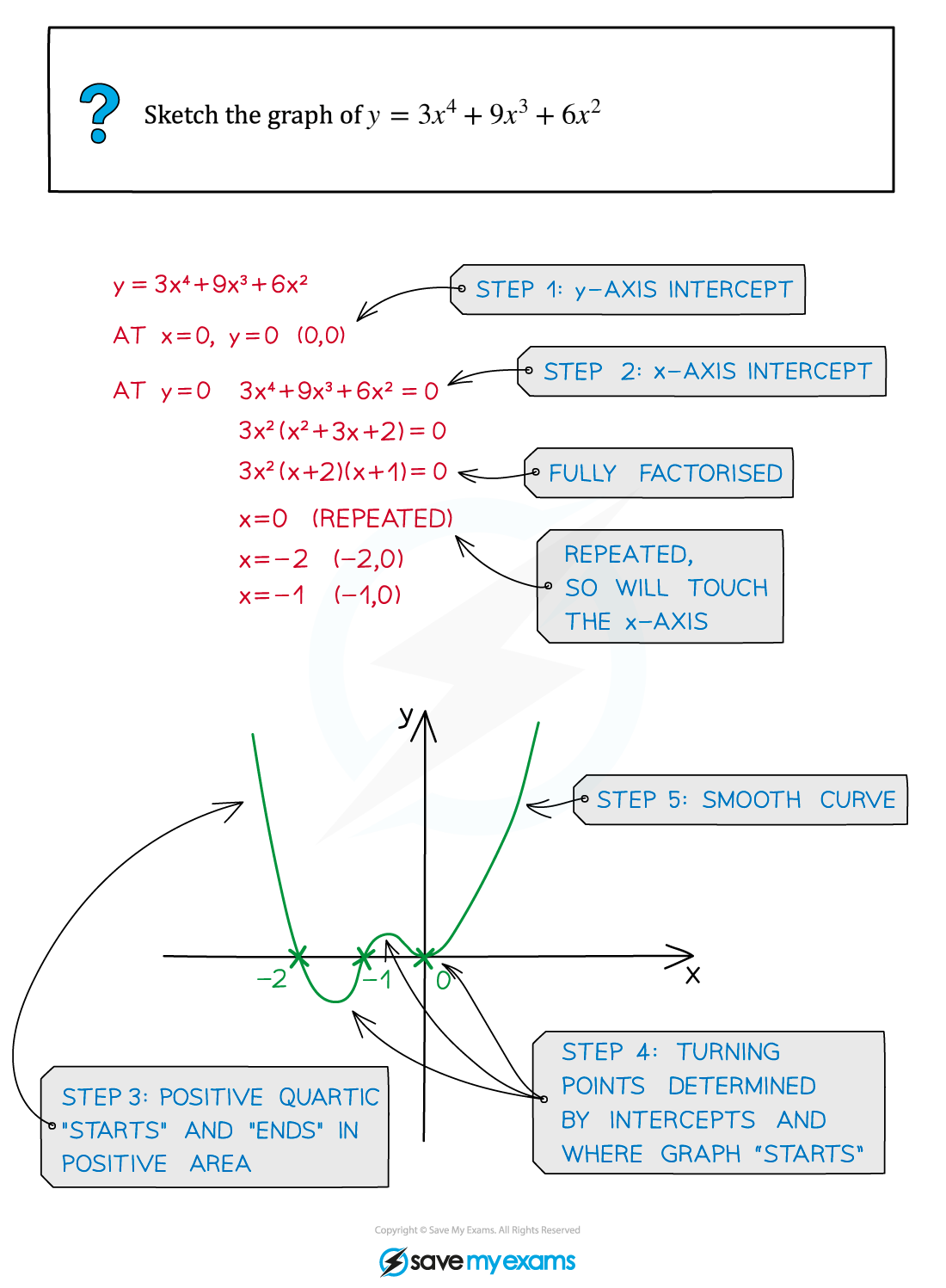
Worked Example

Unlock more, it's free!
Was this revision note helpful?
