Linear Inequalities (Cambridge (CIE) A Level Maths) : Revision Note
Did this video help you?
Linear Inequalities
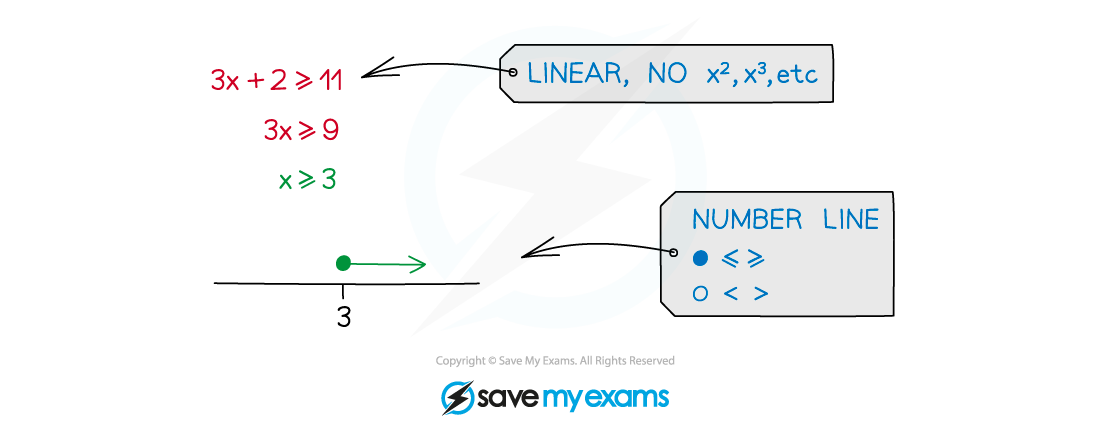
Linear inequalities
Similar to equations but answers take a range of values
Linear means there will be no terms other than degree 1
no squared terms or higher powers, no fractional or negative powers
Number line diagrams are often used
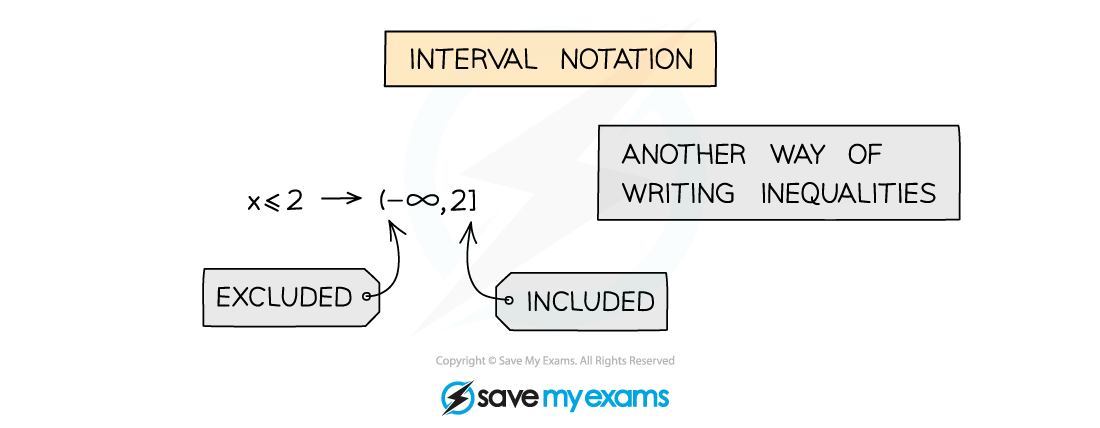
Interval notation
Use of square [] and round () brackets
[ or ] mean included
( or ) mean excluded
(4,8] means 4 < x < 8
Note ∞ always uses ( or )
How do I solve linear inequalities?
treat as equations but
avoid multiplying or dividing by a negative
if unavoidable, “flip” the inequality sign so < → >, ≥ → ≤, etc
do rearrange to make the x term positive

Worked Example


You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?
