Approximations of Distributions (Cambridge (CIE) A Level Maths) : Revision Note
Did this video help you?
Normal Approximation of Poisson
When can I use a normal distribution to approximate a Poisson distribution?
A Poisson distribution
can be approximated by a normal distribution
provided
is sufficiently large ( > 15)
Remember that the mean and variance of a Poisson distribution are approximately equal, therefore the parameters of the approximating distribution will be:
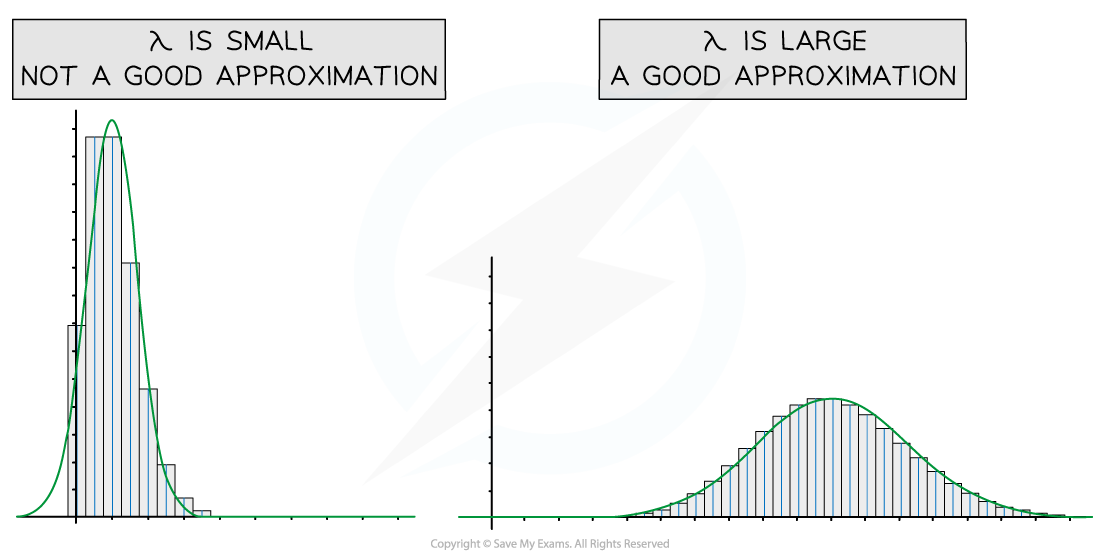
The greater the value of λ in a Poisson distribution, the more symmetrical the distribution becomes and the closer it resembles the bell-shaped curve of a normal distribution
What are continuity corrections?
The Poisson distribution is discrete and the normal distribution is continuous
A continuity correction takes this into account when using a normal approximation
The probability being found will need to be changed from a discrete variable, X to a continuous variable, XN
For example, X = 4 for Poisson can be thought of as
for normal as every number within this interval rounds to 4
Remember that for a normal distribution the probability of a single value is zero so
Do I need to use continuity corrections?
Yes!
As the Poisson distribution X is discrete and normal distribution XN is continuous you will need to use continuity corrections
How do I approximate a probability?
STEP 1: Find the mean and variance of the approximating distribution
STEP 2: Apply continuity corrections to the inequality
STEP 3: Find the probability of the new corrected inequality
Find the standard normal probability and use the table of the normal distribution
The probability will not be exact as it is an approximation but provided λ is large enough (approximately > 15) then it will be a close approximation
Worked Example
The number of hits on a revision web page per hour can be modelled by the Poisson distribution with a mean of 40. Find the probability that there are more than 50 hits on the webpage in a given hour.

Did this video help you?
Poisson Approximation of Binomial
When can I use a Poisson distribution to approximate a binomial distribution?
A binomial distribution B(n,p)can be approximated by a Poisson distribution provided
n is large ( typically > 50 )
p is small
np is approximately less than 5
The mean of a binomial distribution can be calculated by:
The Poisson distribution is derived from the binomial distribution for conditions where n is becoming infinitely large and p is becoming infinitely small
Do I need to use continuity corrections?
No!
As both the binomial distribution and Poisson distribution are discrete there is no need for continuity corrections
Worked Example
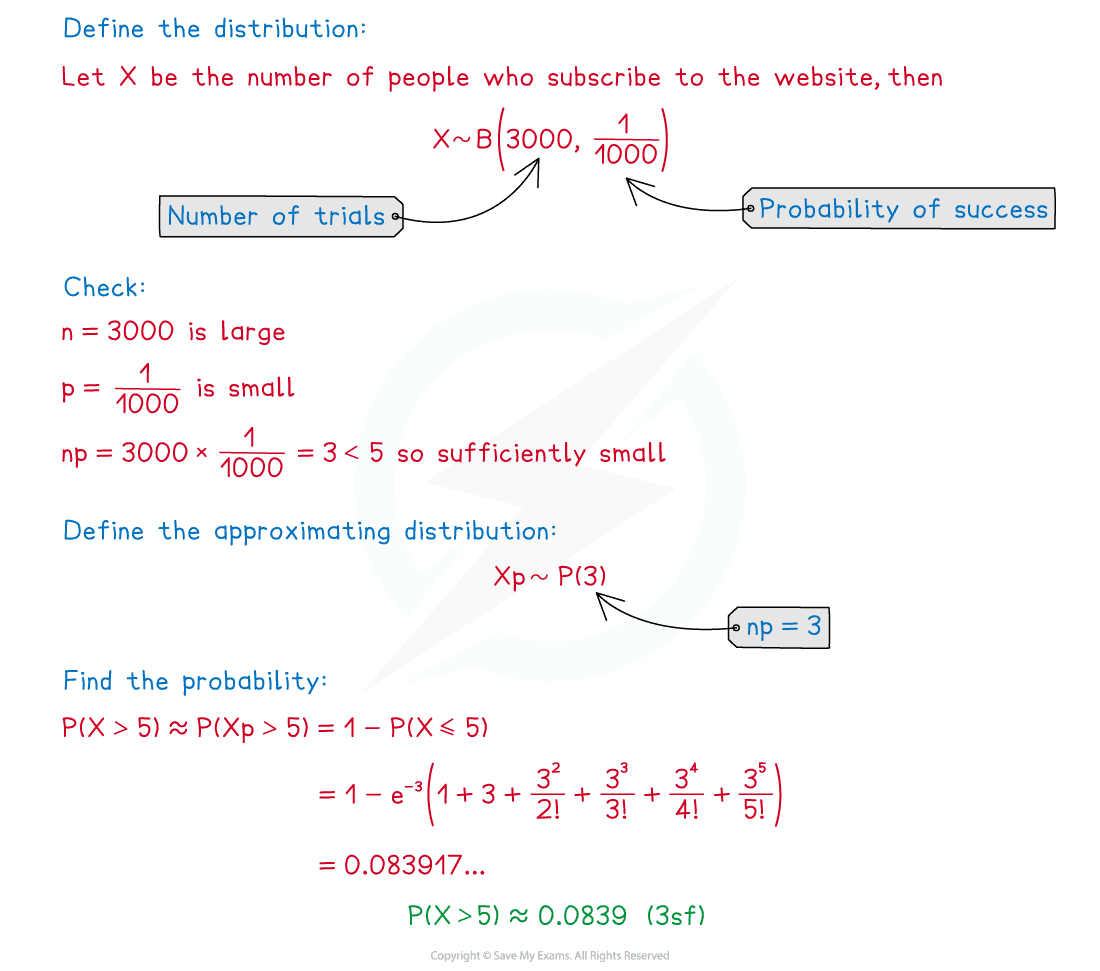
It is known that one person in a thousand who checks a revision website will choose to subscribe. Given that the website received 3000 hits yesterday, find the probability that more than 5 people subscribed.
Did this video help you?
Choosing the Approximation
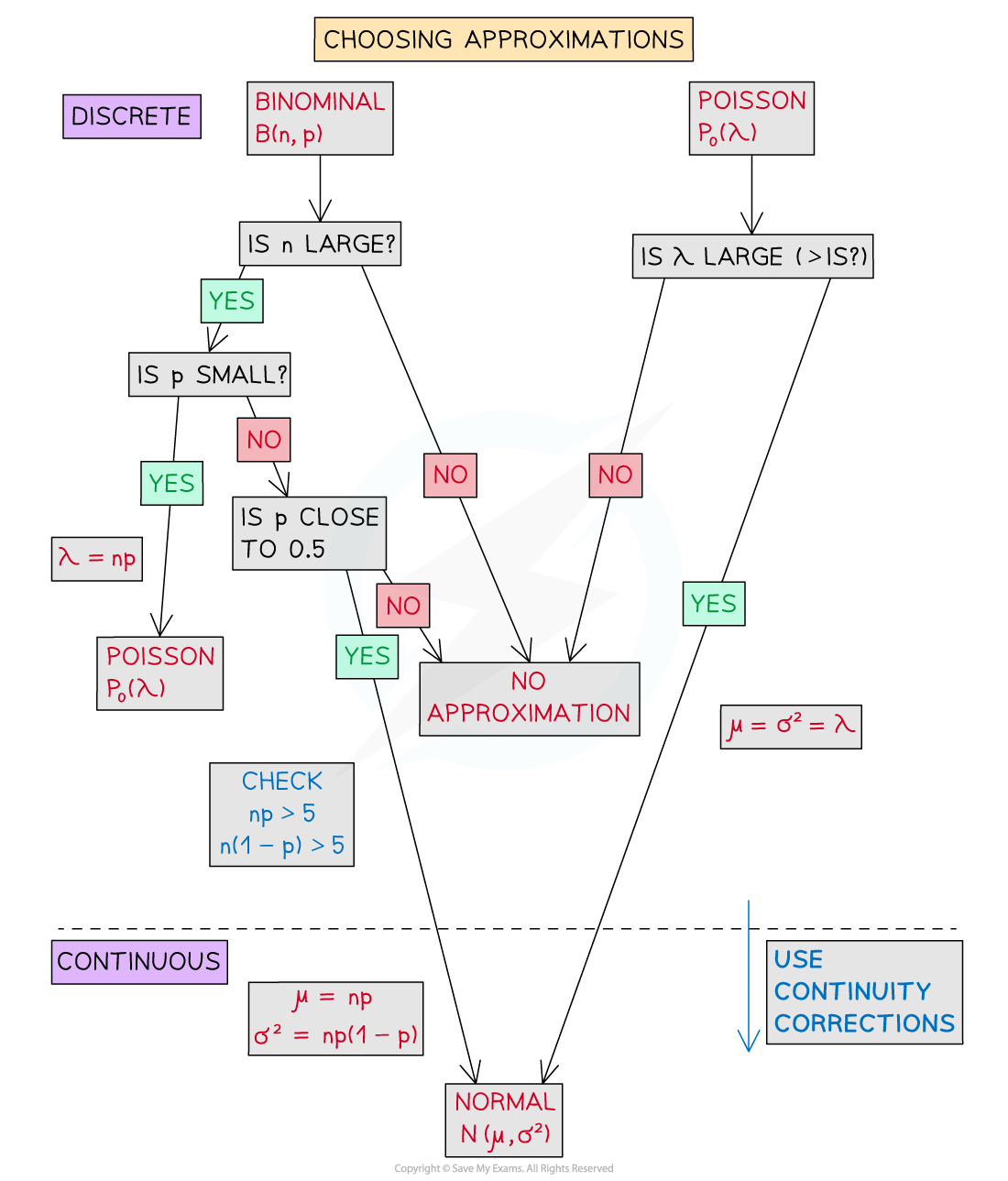
How will I choose which approximation to use?
When deciding what approximating distribution to use first make sure you know the reason why you cannot find the probability using the original distribution
Is the value of n or λ too large?
Will it take too long to carry out the calculations?
Make sure you know what distribution you are approximating from
If your distribution is a binomial distribution, you could either use a Poisson or a normal approximation
If your distribution is a Poisson distribution, you will use a normal approximation
Use the conditions for approximations to decide which approximation is appropriate
Calculate the parameters for the approximating distribution
Examiner Tips and Tricks
If you are unsure, use the normal distribution to approximate the Poisson and the Poisson distribution to approximate the binomial as these are the two you will be examined on in Statistics 2. However, you should make sure you know the conditions for the normal approximation to the binomial as this may be tested.

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?
