Tree Diagrams with Conditional Probability (Cambridge (CIE) A Level Maths): Revision Note
Exam code: 9709
Did this video help you?
Further Tree Diagrams
What do you mean by further tree diagrams?
The tree diagrams used here are no more complicated than those in the first Tree Diagrams revision note, however
questions may use set notation as well, or alongside contextual questions
(union),
(intersection) , ‘ (complement), | ("given that")
more detailed use of conditional probability
three events for each experiment and three experiments could be used
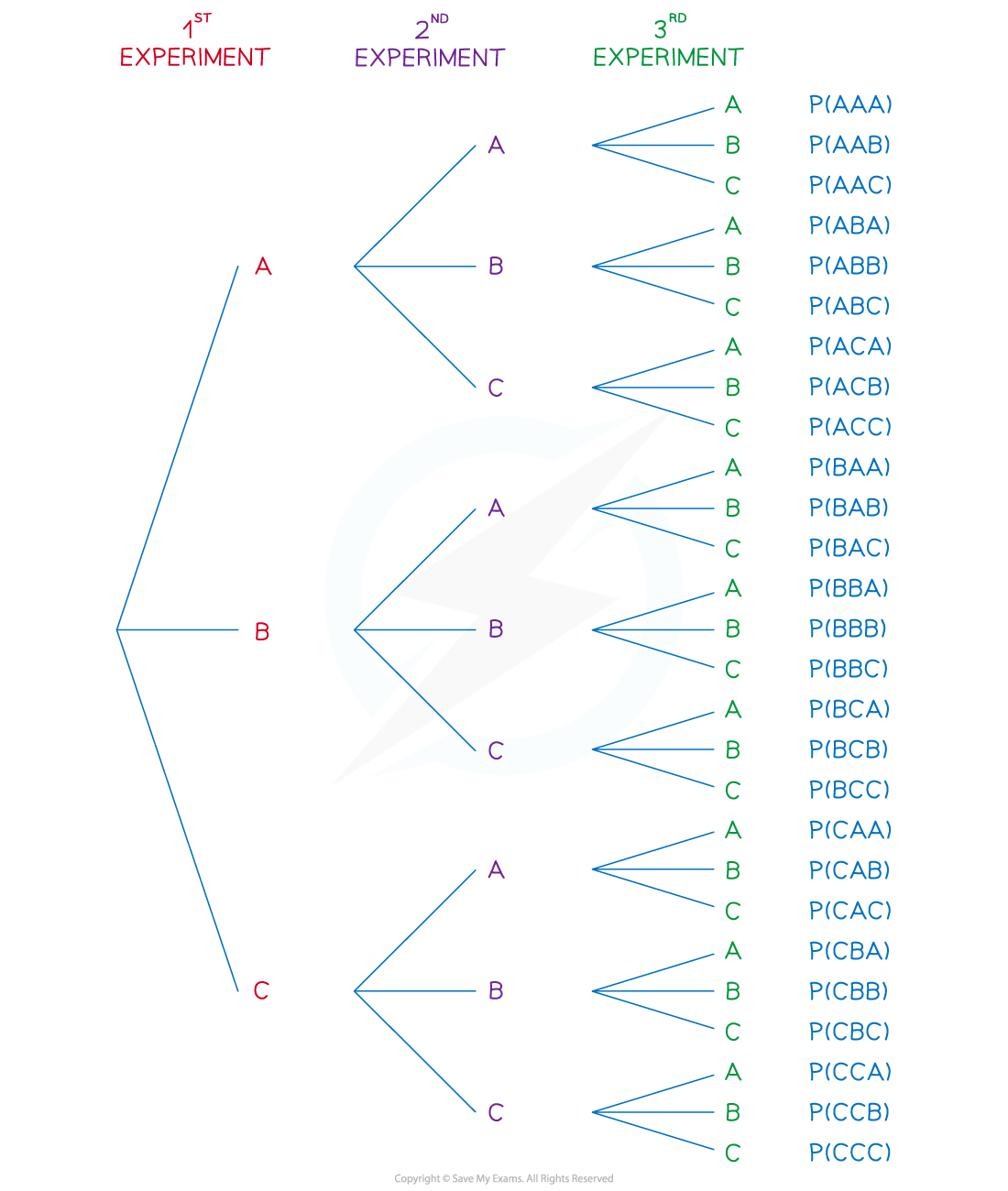
How do I solve conditional probability problems using tree diagrams?
Interpreting questions in terms of AND (
), OR (
), complement ( ‘ ) and “given that” ( | )
Condition probability may now be involved too
This makes it harder to know where to start and how to complete the probabilities on a tree diagram
e.g. If given, possibly in words,
then event A has already occurred so start by looking for the branch event A in the 1st experiment, and then P(B | A) would be the branch for event B in the 2nd experiment
Similarly, would require starting with event “
” in the 1st experiment and event B in the 2nd experiment

The diagram above gives rise to some probability formulae you will see in Probability Formulae
(“given that”) is the probability on the branch of the 2nd experiment
However, the “given that” statement
is more complicated and a matter of working backwards
from Conditional Probability,
from the diagram above,
leading to
This is quite a complicated looking formula to try to remember so use the logical steps instead – and a clearly labelled tree diagram!
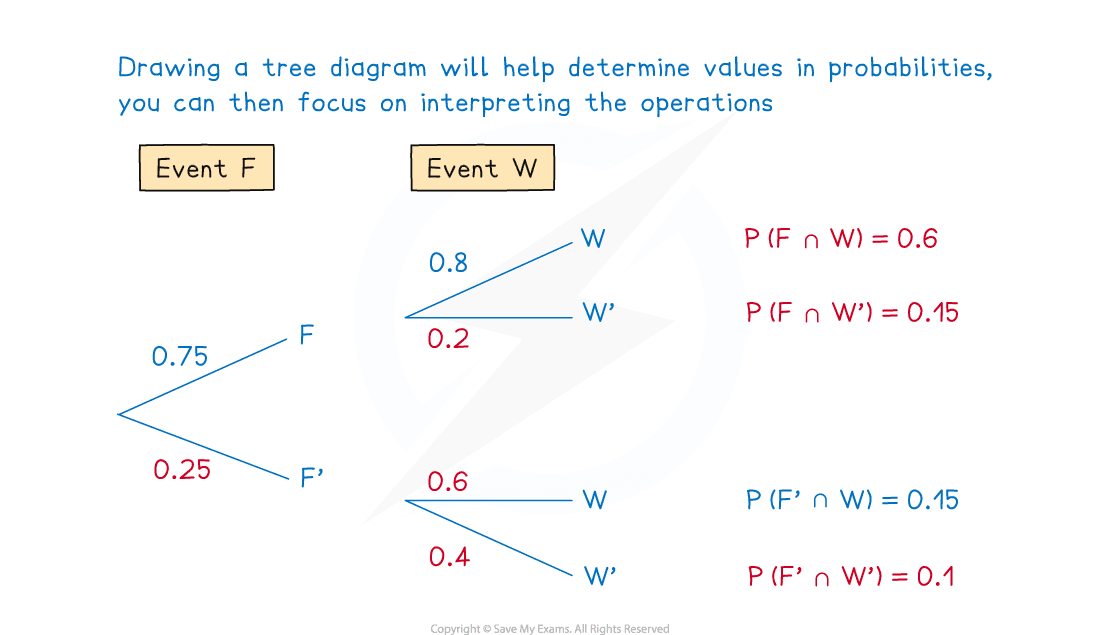
Worked Example
The event has a 75% probability of occurring.
The event follows event
, and if event
has occurred, event
has an 80% chance of occurring.
It is also known that .
Find
(i)
(ii)
(iii) the probability that event didn’t occur, given that event
didn’t occur.

Examiner Tips and Tricks
Be wary of assuming that “given that” statements will always be referring to something on the second set of branches (2nd experiment), they can work the other way!

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?