Coding Data (Cambridge (CIE) A Level Maths): Revision Note
Exam code: 9709
Did this video help you?
Coding
Sometimes data needs to be coded for further use with calculations. This is particularly useful with data that deals with very small or very large numbers, or with data that needs to be classified for research purposes.
What is coding?
Coding is a way of simplifying data to make it easier to work with
The coding must be carried out on all values within the data set and will normally be done using a given formula
Coding can be carried out in a number of ways:
Adding or subtracting a constant to each data value
Multiplying or dividing each data value by a constant
A combination of both of the above
You may occasionally see coding called an assumed mean
This refers to the value chosen to subtract from the original data
It is usually chosen as an easy value, similar to an estimate of the true mean
How are statistical calculations carried out with coded data?
If you know the mean or standard deviation of the original data it is possible to find the mean or standard deviation of the coded data and vice versa
It is important to remember what the mean and standard deviation actually tell us about the data to understand how coding calculations work
The mean is a measure of location, changing the data set in any way will cause the mean to change in the same way
The standard deviation is a measure of spread, adding or subtracting a constant to every value within the data set will not change the standard deviation of the data set
Multiplying or dividing every value within the data set by a constant will change the standard deviation by the modulus of the constant
If the data were coded by multiplying or dividing by a negative, the standard deviation will change by the equivalent positive value
Anytime calculations are carried out on data that has been coded,
The original mean can be found by solving the equation to reverse the coding
For example, if the data,
, was coded using the formula
Then the mean of the coded data, would be
The original mean, , will be
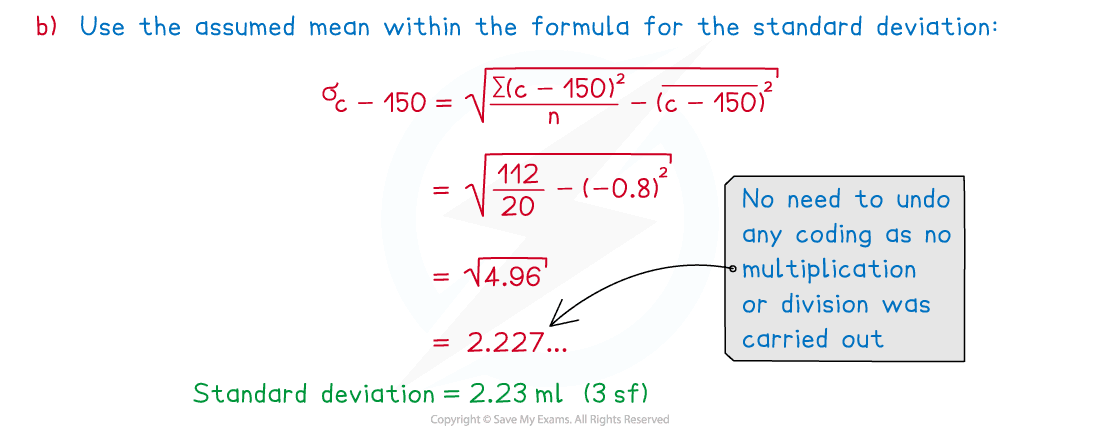
The original standard deviation
Will be the same as the coded standard deviation if the data was coded by adding or subtracting a constant only
Can be found by reversing the coding if the data was coded by multiplying or dividing by a constant only
If the data was coded by a combination of both then only the multiplying or dividing will need to be reversed to find the original standard deviation
For example, if the data,
, was coded using the formula
Then the standard deviation of the coded data, would be
The original standard deviation, , will be
What will summary statistics and formulae look like with an assumed mean?
If an assumed mean, a, has been subtracted from all data values, x, then the summary statistics for the coded data will be
The sum of the coded data
The sum of the squares of the coded data
Be careful not to mix this up with the square of the sum of the coded data
If an assumed mean, a, has been subtracted from all data values, x, then the formulae for the mean and standard deviation for the coded data will be
Most questions will give you either the summary statistics or the mean of the coded data and expect you to work with these formulae to find original information about the data
Worked Example
A coffee machine is set to dispense 150 ml of coffee per cup.
In a random sample of 20 cups of coffee , where
ml is the volume of coffee in a cup.
(a) Find the mean volume in a cup of coffee.
(b) Given that , find the standard deviation of the sampled cups of coffee.
Answer:
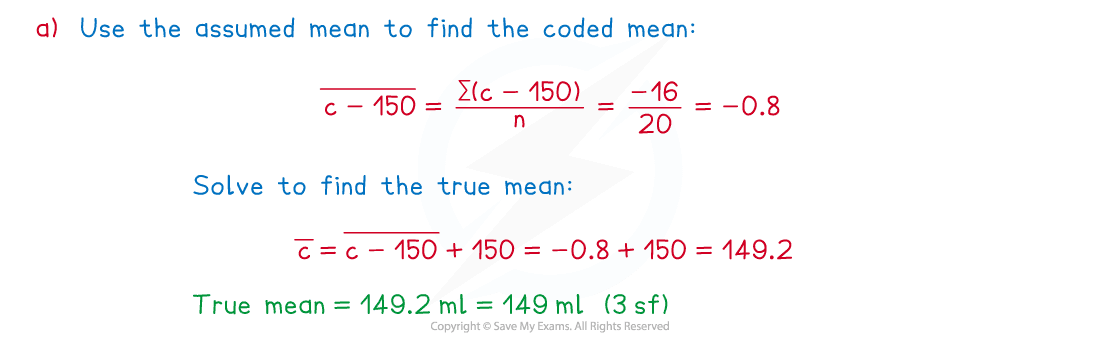
Examiner Tips and Tricks
Be careful when using the formulae for the mean and standard deviation with coded summary statistics, you must make sure that you use the summary statistics consistently throughout. For example, if you use the sum of the coded data squared in the formula for the standard deviation, you must subtract the square of the coded mean.

Unlock more, it's free!
Did this page help you?