Working with Vectors (Edexcel A Level Maths: Mechanics)

Vectors are used throughout mechanics to describe forces and motion

 How are Vectors used in Mechanics?

• Vector questions are often embedded in a Mechanics context
• Vectors will most commonly represent forces, accelerations or velocities, they can also represent displacement
• Newton’s Second Law is essential
  • Remember that and (force and acceleration) are vectors, while  (mass) is a scalar
• When a particle is in equilibrium, the vector sum of the forces on it is equal to zero

What is vector notation?

• There are two vector notations used in A level mathematics:
  • Column vectors: This is one number written above the other enclosed in brackets,

e.g. The (column) vector meaning 3 units in the positive horizontal (x) direction (i.e., right) and 2 units in the negative vertical (y ) direction (i.e., down) can be written as:

• • i and j notation: i and j are unit vectors (they have magnitude 1) in the positive horizontal and positive vertical directions respectively

e.g. The vector (-4i + 3j) would mean 4 units in the negative horizontal (x) direction (i.e. left) and 3 units in the positive vertical (y) direction (i.e. up)

• As they are vectors, i and j are displayed in bold in textbooks and online but in handwriting they would be underlined (i and j)

Calculating Resultant Vectors:

• Both column vectors and i, j notation can be used for calculating resultant vectors
• Adding vectors together gives the resultant vector
• This is the same when adding force vectors; the resultant force is simply the force vectors added together
• Forces in equilibrium have a resultant force equal to zero

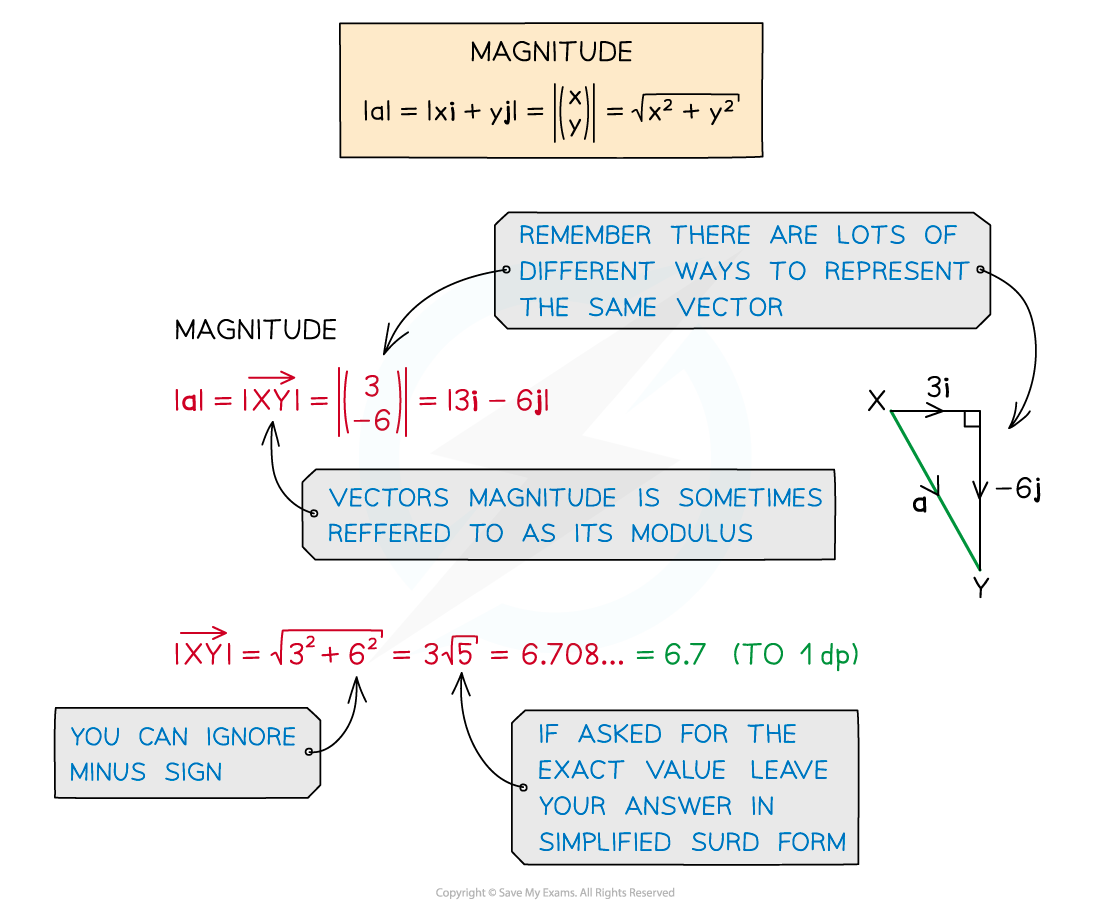
Calculating Magnitude and Direction:

• Pythagoras is used to find the magnitude of a vector.
• Trigonometry is used to find the direction of a vector
• You may be asked for the direction as a bearing. The unit vector j can be used to represent north and the unit vector i can be used to represent east.
  • In the case where k > 0
    • If a particle is moving north then its velocity will have a vector of kj
    • if a particle A is due south of another particle B then the displacement vector from B to A will have the form -kj
    • If a particle is moving east then its velocity will have a vector of ki
    • if a particle A is due west of another particle B then the displacement vector from B to A will have the form -ki
  • If the position vectors of two particles have the same j component, then the particle with the greater i component will be positioned due east of the other
  • If the position vector of a particle has equal i and j components then it is positioned due north - east of the origin
    • if a particle A is north – east of another particle B then the displacement vector from B to A will have equal i and j components

Resolving Vectors:

• Resolving a vector means writing it in component form (as i and j components)
• Given the magnitude and direction of a vector you can work out its components and vice versa

a)  Find the magnitude of the resultant force R acting on the particle.

     Leaving your answer as a simplified surd.

b)  Find the bearing of the resultant force R.

     Give your answer to the nearest degree.

A third force F₃ = si – tj brings the particle into equilibrium.

c)   Find s and t and state the force for F₃ in terms of i and j.