Newton’s Second Law of Motion describes the motion of bodies under the influence of external forces. In one dimension it may be expressed in the form
where is the mass of the body,
is the acceleration it experiences, and
is the total force acting on the body.
In working with this equation, it is important to choose one direction to be the ‘positive’ direction in your workings, with the opposite direction then becoming the ‘negative’ direction. Forces in the negative direction are then subtracted from forces in the positive direction to find the total force. It will often be easiest to choose the direction in which a body is accelerating as the ‘positive’ direction.
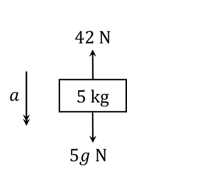
In each of the scenarios depicted below, the forces acting on the body cause it to accelerate as shown. The acceleration due to gravity is indicated by .
By rearranging as appropriate, find the value of the unknown variable – acceleration (
), mass (
) or force (
) – in each case.
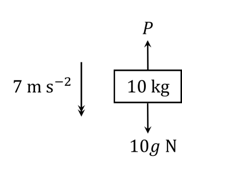
(ii)
Did this page help you?


















