Coefficient of Friction (Harder Problems) (Cambridge (CIE) A Level Maths) : Revision Note
Did this video help you?
Coefficient of Friction - Equilibrium
How is friction used when a body is in equilibrium?
When a body is in static equilibrium under the action of a number of forces, including friction, the value of friction will be less than or equal to the value of μR
When the value of friction is equal to μR, the body is in limiting equilibrium and is on the point of moving
When a body is stationary on an inclined plane then it is either in equilibrium or in limiting equilibrium, we cannot assume that F = μR
How is friction used when a body is moving?
When a body is moving under the action of a number of forces, including friction, the value of friction will be equal to the value of μR
Worked Example
A wooden block of mass m is stationary on a plane inclined at 25° above the horizontal. The coefficient of friction between the block and the plane is µ. Find the least possible value of µ .
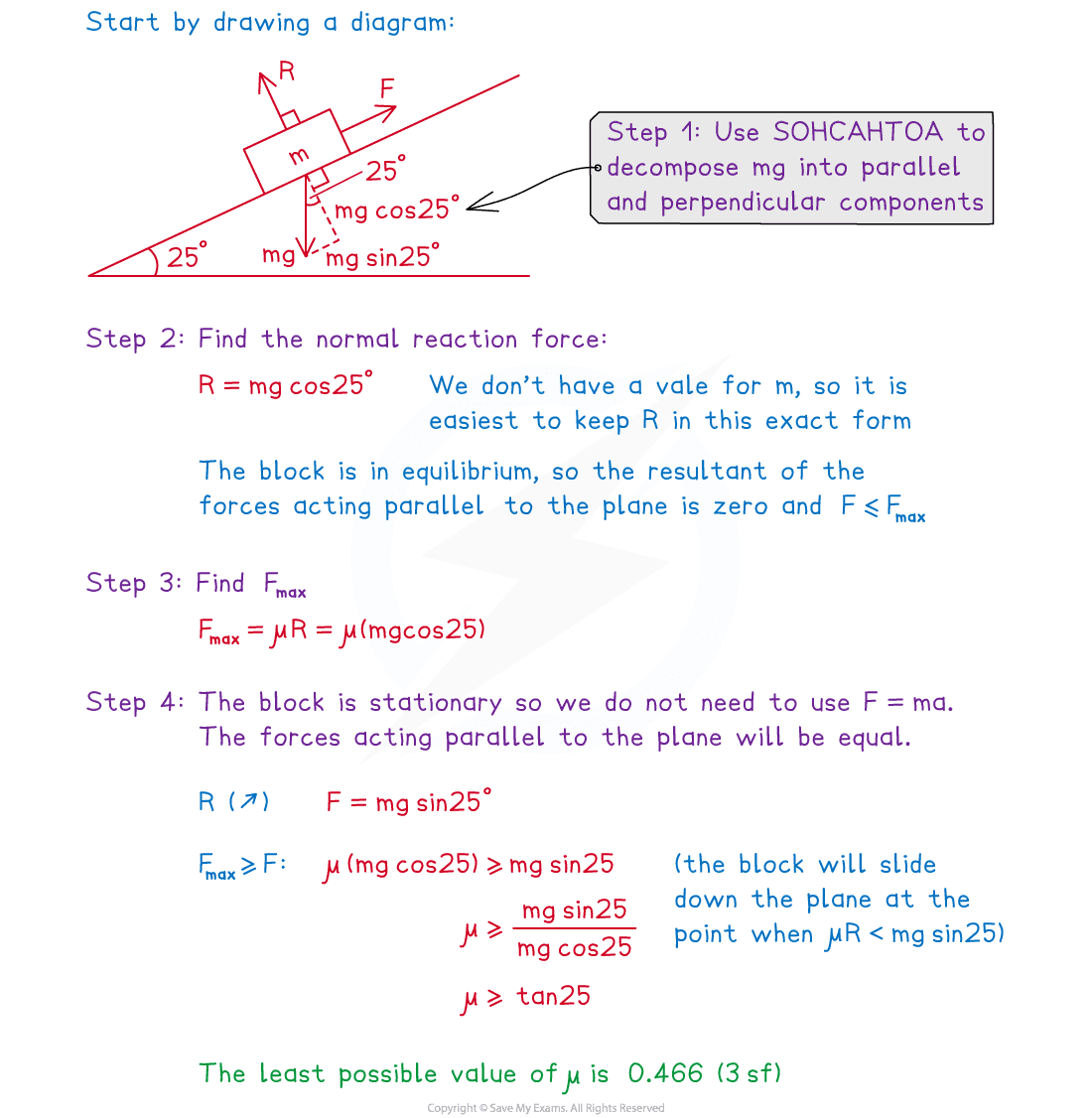
Examiner Tips and Tricks
Always draw a force diagram and label it clearly.
Look out for key vocabulary such as rough, smooth, equilibrium, on the point of moving and limiting equilibrium and know how to use each.
Did this video help you?
Coefficient of Friction – Connected Particles
How is friction used for connected particles?
When two particles are connected by means of a light, inextensible string, friction will act only on any particle that is resting on a rough surface
On an inclined slope, friction will act in the direction opposite to the direction the particle is moving in or on the point of moving in
The direction they will move in depends on both the weight of the particles and the angles of the slopes they are resting on
Compare the components of the weight in the direction of the motion the particles will move in
The particle with the heavier component will move down the slope
Worked Example
Two particles A and B, of identical mass, are connected by means of a light inextensible string Particle A is held motionless on a rough fixed plane inclined at 30o to the horizontal. Particle B is resting on a rough fixed plane inclined at 60o to the horizontal. The string passes over a smooth light pulley fixed at the top of the two planes as shown in the diagram below.

Given that the coefficient of friction between particle A and the plane is 0.2 and that the particles are in limiting equilibrium, show that particle A is on the point of moving down the slope and find the value of the coefficient of friction between particle B and the plane.
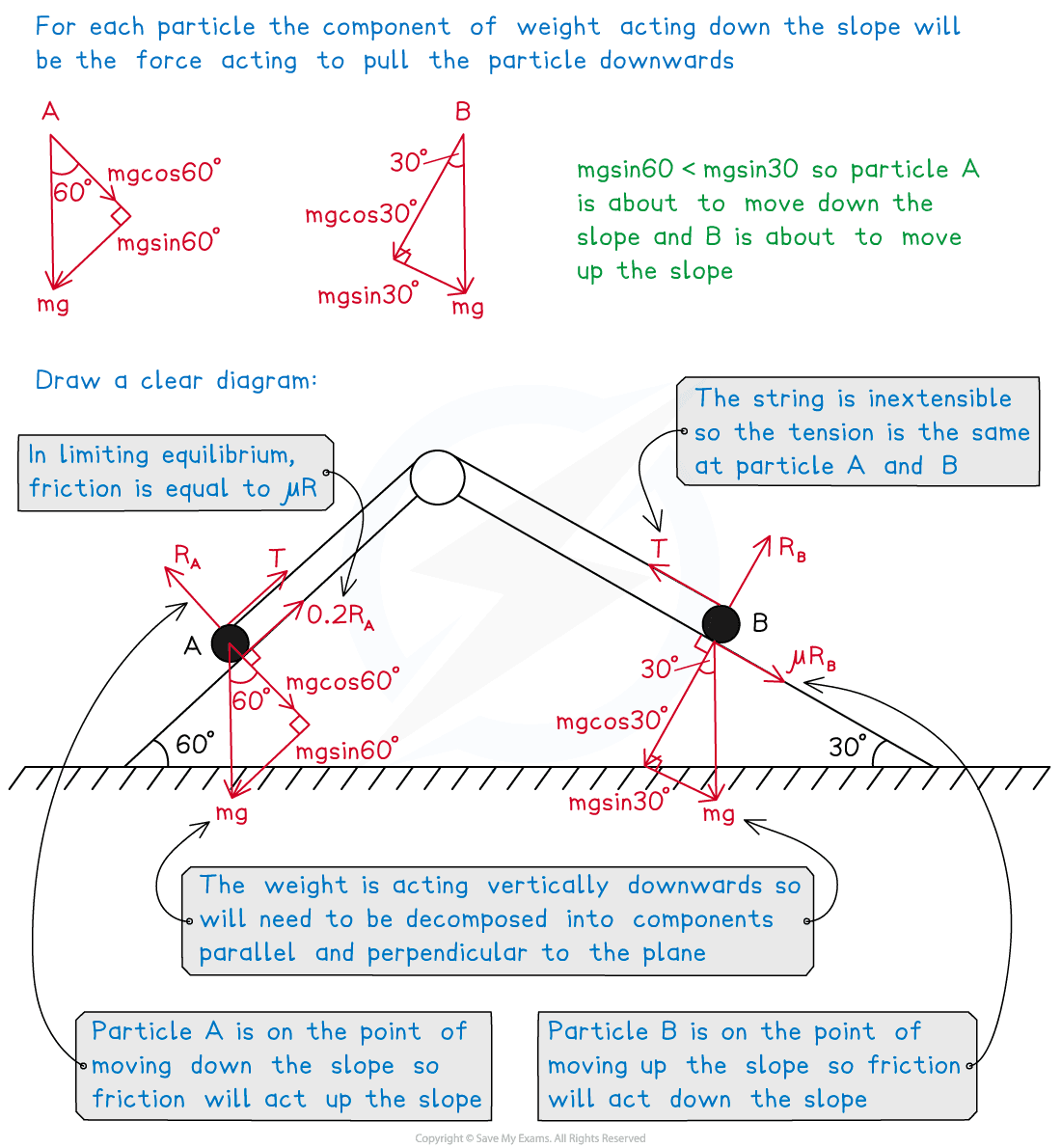

Examiner Tips and Tricks
Be careful not to assume that the system will move in the direction of the heavier particle, remember to consider the angle too. Make sure your diagram is clear enough to work with, sometimes there can be a lot of information on the diagram.

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
