Connected Bodies - Pulleys | CIE A Level Maths: Mechanics Revision Notes 2020

Connected Bodies - Pulleys

A pulley is a wheel like device that rotates as a string passes over it allowing motion of any particles attached to the string
- The term ‘string’ can refer to any rope, cable or chain
- Strings can be assumed to be light and inextensible
Pulleys allow a (inextensible) string to change its orientation.
In A level mathematical models, pulleys will always be smooth and light, so there is no friction involved at the pulley and its mass is negligible
A peg is similar to a pulley but is a fixed point that a particle can be suspended from (like a nail in a wall)

3-2-4-fig1-pulley-examples

In all pulley questions the particles are moving in different directions so it is best if they are considered separately as opposed to treating them as one object
If a particle is in motion in the direction being considered then Newton’s Laws of Motion apply so use “F = ma” (N2L)
For constant acceleration the ‘suvat’ equations could be involved
Step 1. Draw a series of diagrams
- Label the forces and the positive direction of motion for each particle.
- Colour coding forces acting on each particle may help
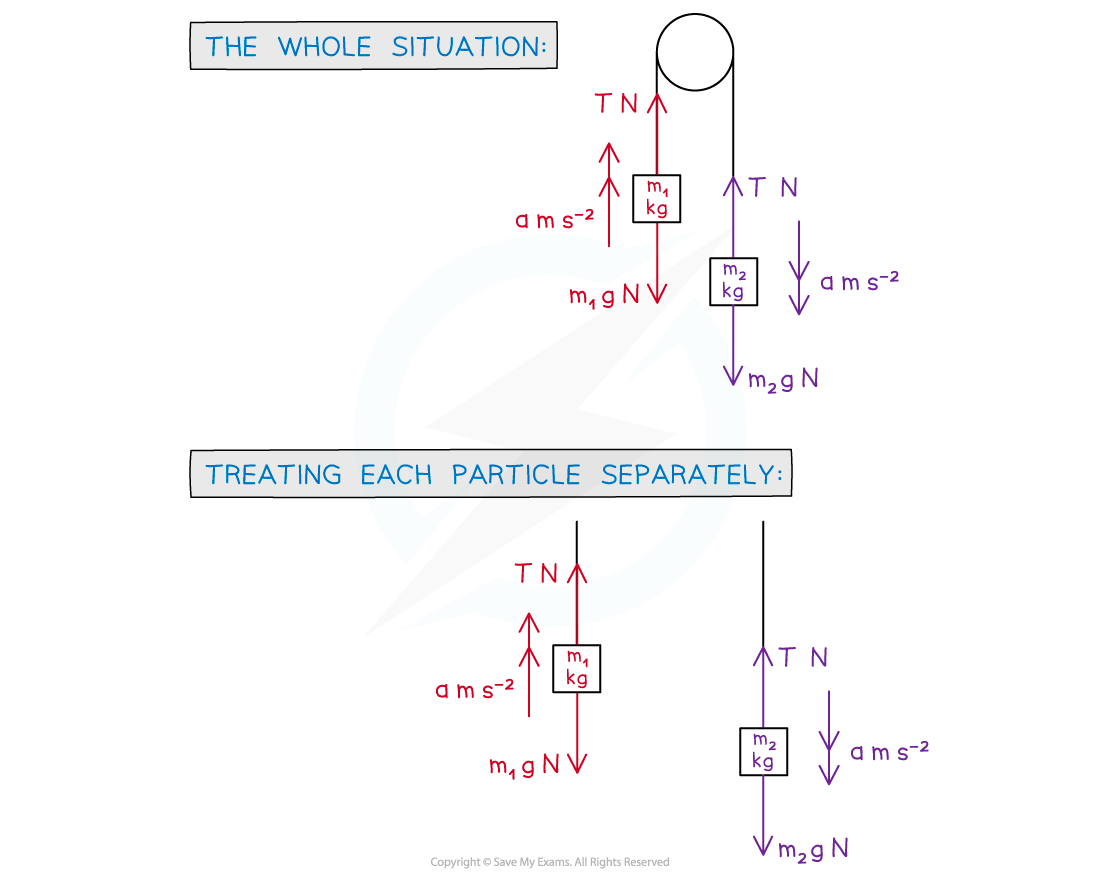
Step 2. Write equations of motion, using “F = ma”
- Equations 1 and 2: Treating each particle separately

(↑) $T - m_{1} g = m_{1} a$

(↓) $m_{2} g - T = m_{2} a$

Step 3. Solve the relevant equation(s) and answer the question
- Some trickier problems may lead to simultaneous equations

3.2.4_WE_Pulleys_1

Find the tension, T N , in the string and the acceleration, a m s^-2 , of the system.

cie-3-2-4-fig5-we-solution-correction-part-1

cie-3-2-4-fig5-we-solution-correction-part-2

Sketch a diagram or add to a diagram given in a question.
All pulleys are smooth and in most (but not all) the pulley itself can be ignored.
In pulley questions the particles will be moving in different directions - so each particle will need to be considered separately.
If one particle is on a horizontal surface (such as a desk or table) then the weight only need be considered if friction is involved (since F = μR and R is related to weight).