Coefficient of Friction - Inclined Planes (AQA A Level Maths: Mechanics)

How is the coefficient of friction used in problems involving inclined planes?

• On an inclined plane the basic principles are the same as for coefficient of friction on horizontal surfaces
• The important directions are parallel to the plane and perpendicular to the plane (instead of horizontal and vertical)
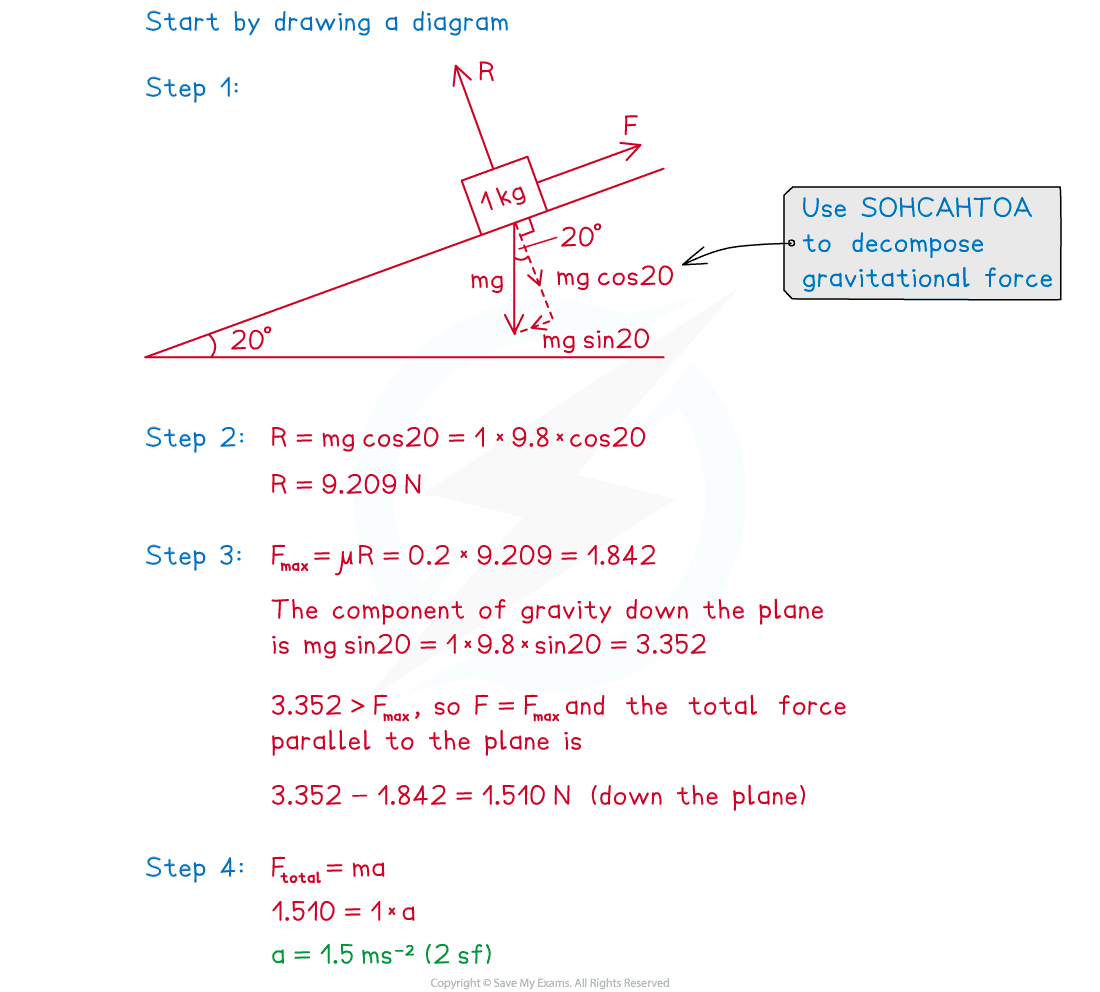
• Step 1. Resolve weight (and any other forces if necessary) into components parallel and perpendicular to the plane
• Step 2. Calculate the normal reaction force R
  • Be careful – R will never simply be equal to mg in an inclined plane problem!
  • R will always be directed perpendicular to and away from the plane
  • the magnitude of R will always be such as to make the total perpendicular force zero
• Step 3. Calculate F_MAX= μR and find the resultant (total force) of all the forces on the object that are parallel to the plane
  • The force of friction F will always act parallel to the plane in the direction opposite to any movement (or potential movement) of the object
  • Remember – if the resultant of the other parallel forces is less than or equal to F_MAX then friction will exactly balance those forces out and the object will remain stationary
• Step 4. Use F = ma to determine the acceleration of the object

A wooden block of mass 1 kg is released from rest on a rough plane that is inclined at 20°  above the horizontal. The coefficient of friction between the block and the plane is 0.2. Find the acceleration of the block.