F = ma - Vector Notation | AQA A Level Maths: Mechanics Revision Notes 2018

F = ma - Vector Notation

The resultant force (F) and acceleration (a) are vectors
- For forces and motion in two dimensions, F N and a m s^-2 will be made up of two components – a horizontal (x-) component and a vertical (y -) component
Displacement , velocity and weight are also vector quantities
Time and mass are scalar quantities
Vectors appear in bold (non-italic) font in textbooks, on exam papers, etc (i.e. F, a) but in handwriting should be underlined (i.e. F , a )

All vectors are written either as column vectors or in i-j format
As a column vector $F = m a$ would look like

(\begin{matrix} F_{x} \\ F_{y} \end{matrix}) = m (\begin{matrix} a_{x} \\ a_{y} \end{matrix})

In i-j notation $F = m a$ would look like
$F_{x} i + F_{y} j = m (a_{x} i + a_{y} j)$

If vectors/2D are being used this will be clear from the information given in the question – any vector quantities will be given as a column vector or written in i-j notation
Remember $F = m a$ is used when motion is involved – equations may come from ‘suvat’ (if the acceleration is constant), or using N2L directly; look for (resultant) force, mass and acceleration being involved
Use $F = m a$ (N2L in 1D) or an appropriate ‘ $s u v a t$ ’ (in 1D) equation to set up and solve separate equations for both the horizontal ( $x$ -) and vertical ( $y$ -) components.

Weight is a force, so it is a vector quantity
- $W = mg N$ where $g m s^{- 2}$ is the acceleration due to gravity
Weight always acts vertically downwards so it only acts in the j-direction

$W = - mg j N$

Treating the two dimensions separately means weight only needs to be considered when looking at the vertical ( $y$ -) direction
Most 2D/vector problems are based on a bird’s-eye view – the two dimensions being left/right and forwards/backwards, so the up/down (third) dimension where weight would apply, is often not involved

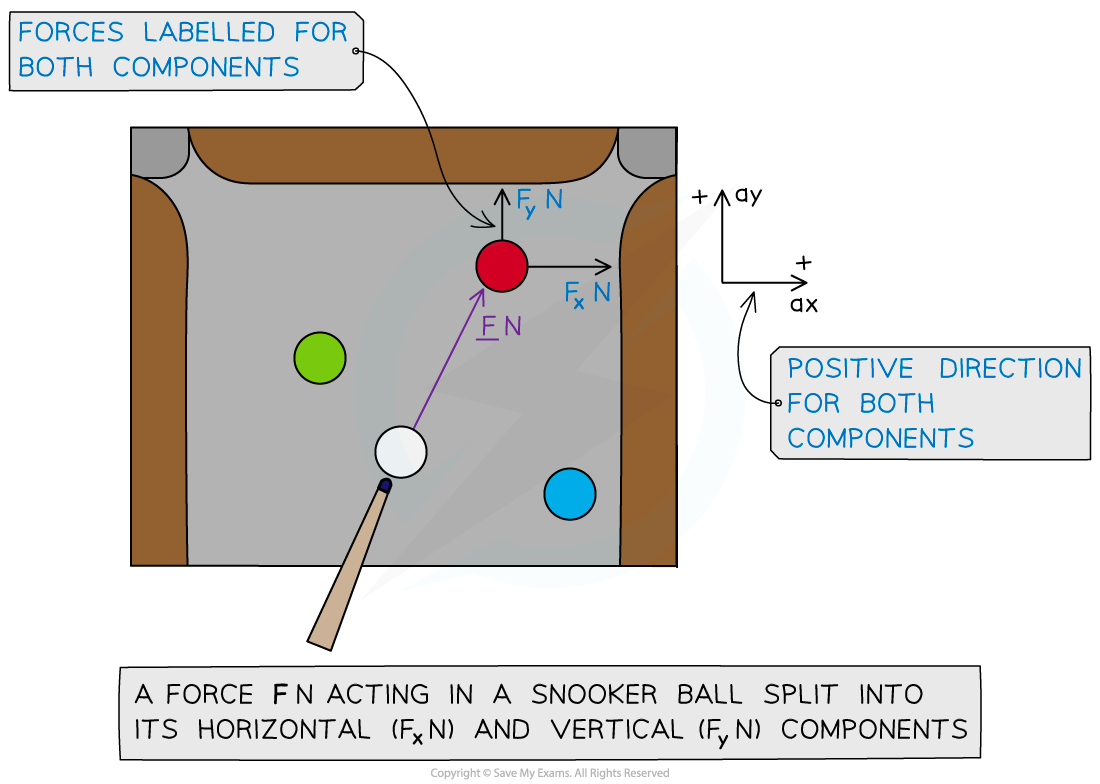
3-2-5-fig1-snooker-ball

Step 1. If necessary, draw a diagram and label all forces acting on the particle(s)
- label the i and j directions and any other useful information.
- If a diagram is given, add any missing information to it.
Step 2. Taking each dimension/component at a time use F = ma
- If there is more than one particle involved you may have to do this for each
Step 3. Solve the equations for each component and put the final answers back into vector notation
- In some harder problems simultaneous equations may arise

3.2.5_WE_F-ma-Vector Notation_1

3-2-5-fig2-we-solution

If not given in the question, draw a diagram; label all forces and the positive direction for both components.
Add to a diagram if given one, do not assume it is complete.
Write a list of the quantities that are given in a question and another list of those you are asked to find. This will help you decide which equation(s) to use.
A third list of the quantities you are not concerned with can help as these may be used to find intermediate results.
Unless told otherwise, use g = 9.8 m s^-2 and round your final answer to two significant figures.
Some questions may direct you to use g = 10 m s^-2 in which case round your final answer to one significant figure.