The figure below shows the curve with equation where
The equation
has only one solution,
You may assume that
is continuous for all values of
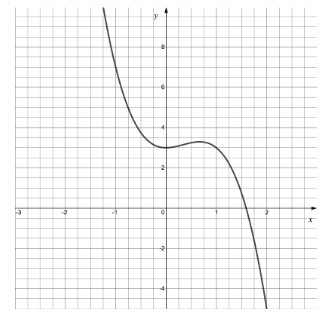
(i) Find
(ii) Find
Use part (a) to write down an interval containing the root , in the form
where and
are constants to be found.
Did this page help you?



























