A bypass is to be built around a village. On the graph below the road through the village is modelled by the line The bypass is modelled by the equation
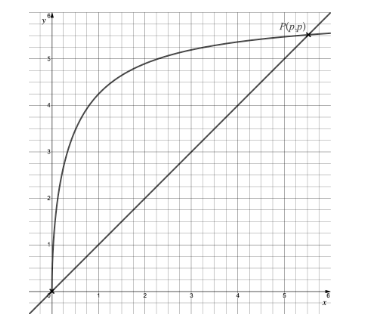
The bypass runs from the origin to the point .
Use the iteration formula
withto find the value of
, correct to 3 significant figures.
Use the interval and the function
to show that your answer to part (a) is correct to 3 significant figures.
Did this page help you?





















