Parametric Differentiation (Edexcel A Level Maths) : Revision Note
Did this video help you?
Parametric Differentiation
How do I find dy/dx from parametric equations?
Ensure you are familiar with Parametric Equations – Basics first
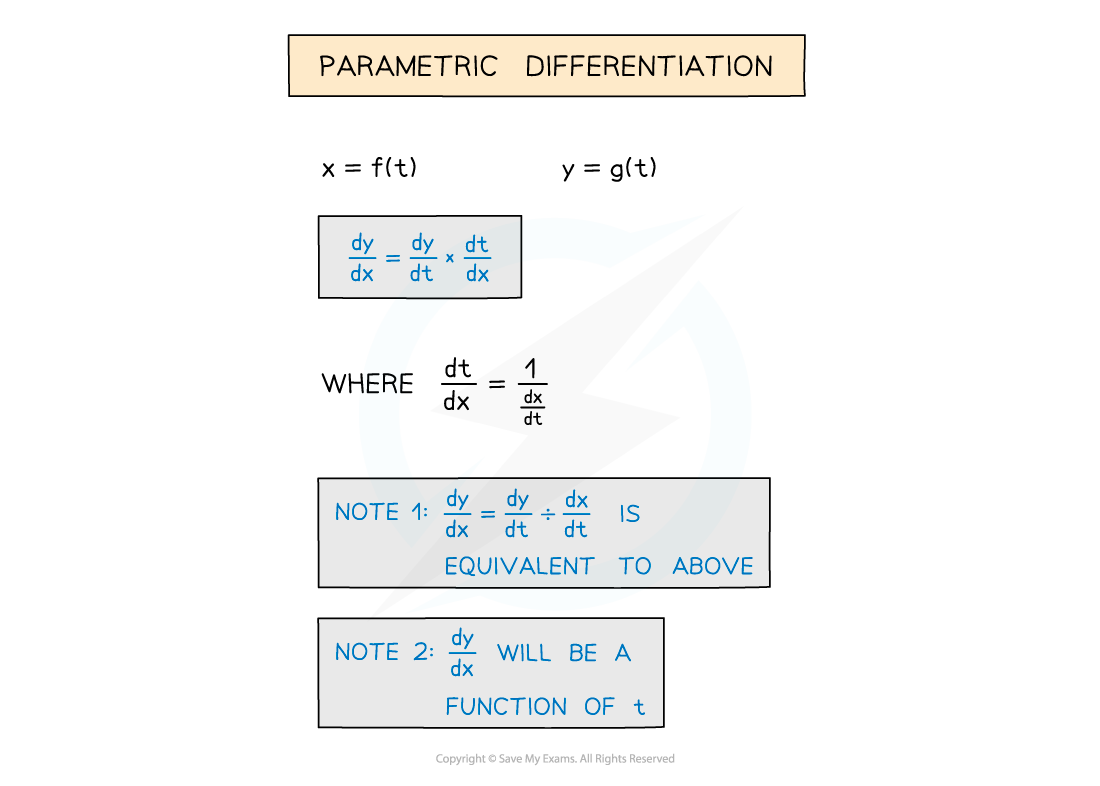
This method uses the chain rule and the reciprocal property of derivatives
Equivalently,
will be in terms of t – this is fine
Questions usually involve finding gradients, tangents and normals
The chain rule is always needed when there are three variables or more – see Connected Rates of Change
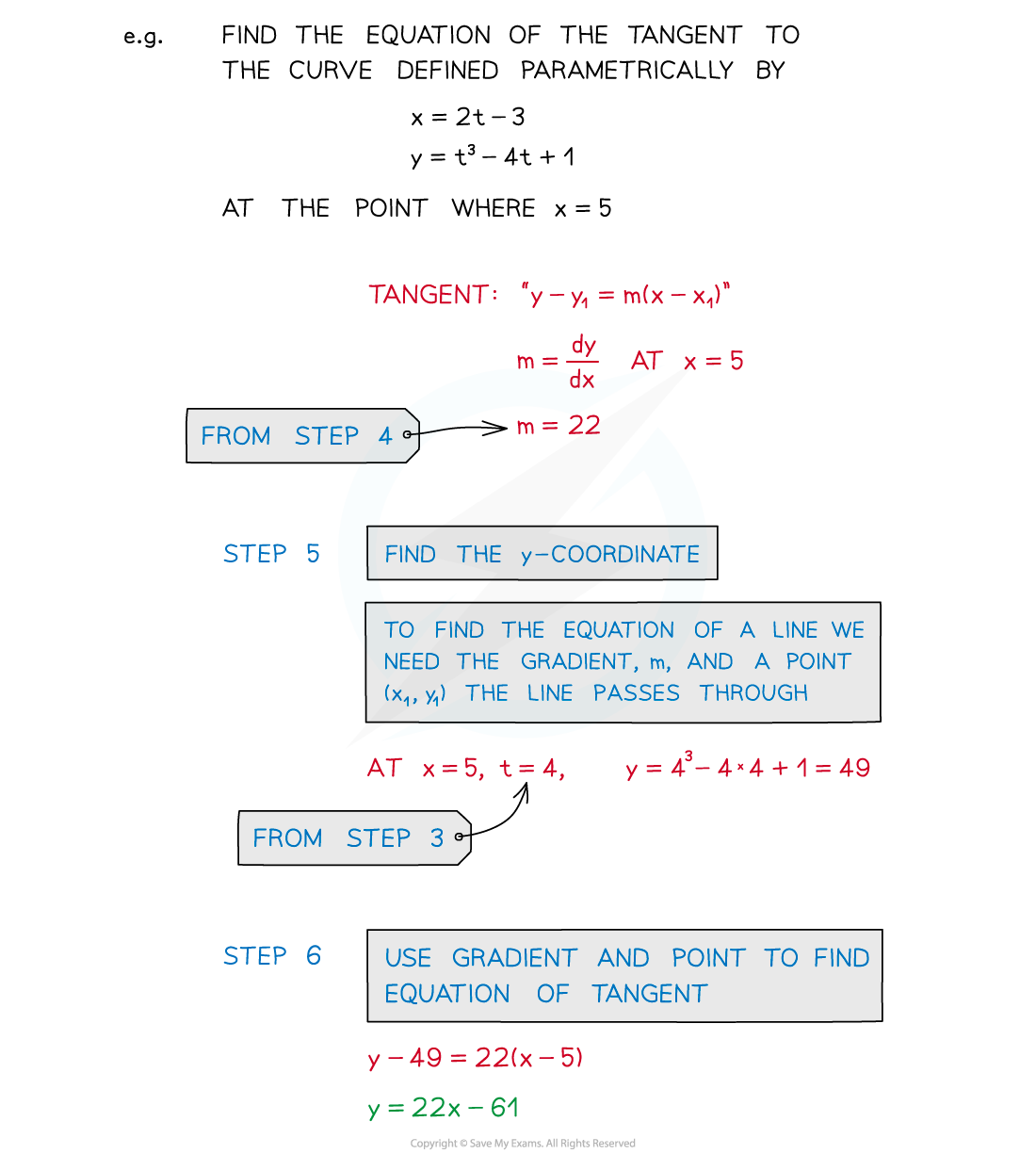
How do I find gradients, tangents and normals from parametric equations?
To find a gradient …
STEP 1: Find dx/dt and dy/dt
STEP 2: Find dy/dx in terms of t
Using either dy/dx = dy/dt ÷ dx/dt
or dy/dx = dy/dt × dt/dx where dt/dx = 1 ÷ dx/dt
STEP 3: Find the value of t at the required point
STEP 4: Substitute this value of t into dy/dx to find the gradient

to then go on to find the equation of a tangent …
STEP 5: Find the y coordinate
STEP 6: Use the gradient and point to find the equation of the tangent
To find a normal...
STEP 7: Use perpendicular lines property to find the gradient of the normal m1 × m2 = -1
STEP 8: Use gradient and point to find the equation of the normal y - y1 = m(x - x1)
What else may I be asked to do?
Questions may require use of tangents and normals as per the coordiante geometry sections
Find points of intersection between a tangent/normal and x/y axes
Find areas of basic shapes enclosed by axes and/or tangents/normal
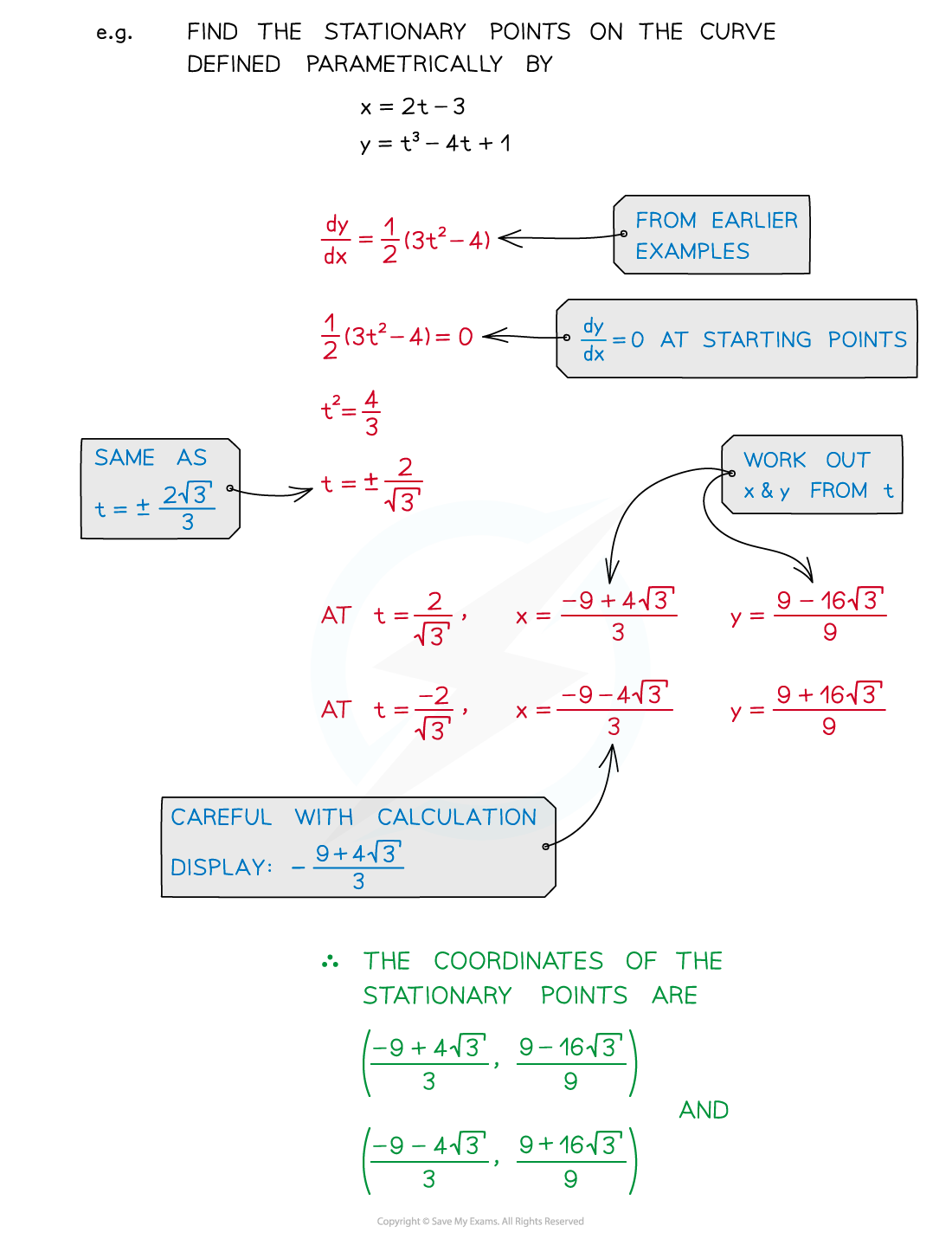
Find stationary points (dy/dx = 0)
You may also be asked about horizontal and vertical tangents
At horizontal (parallel to the x-axis) tangents, dy/dt = 0
At vertical (parallel to y-axis) tangents, dx/dt = 0
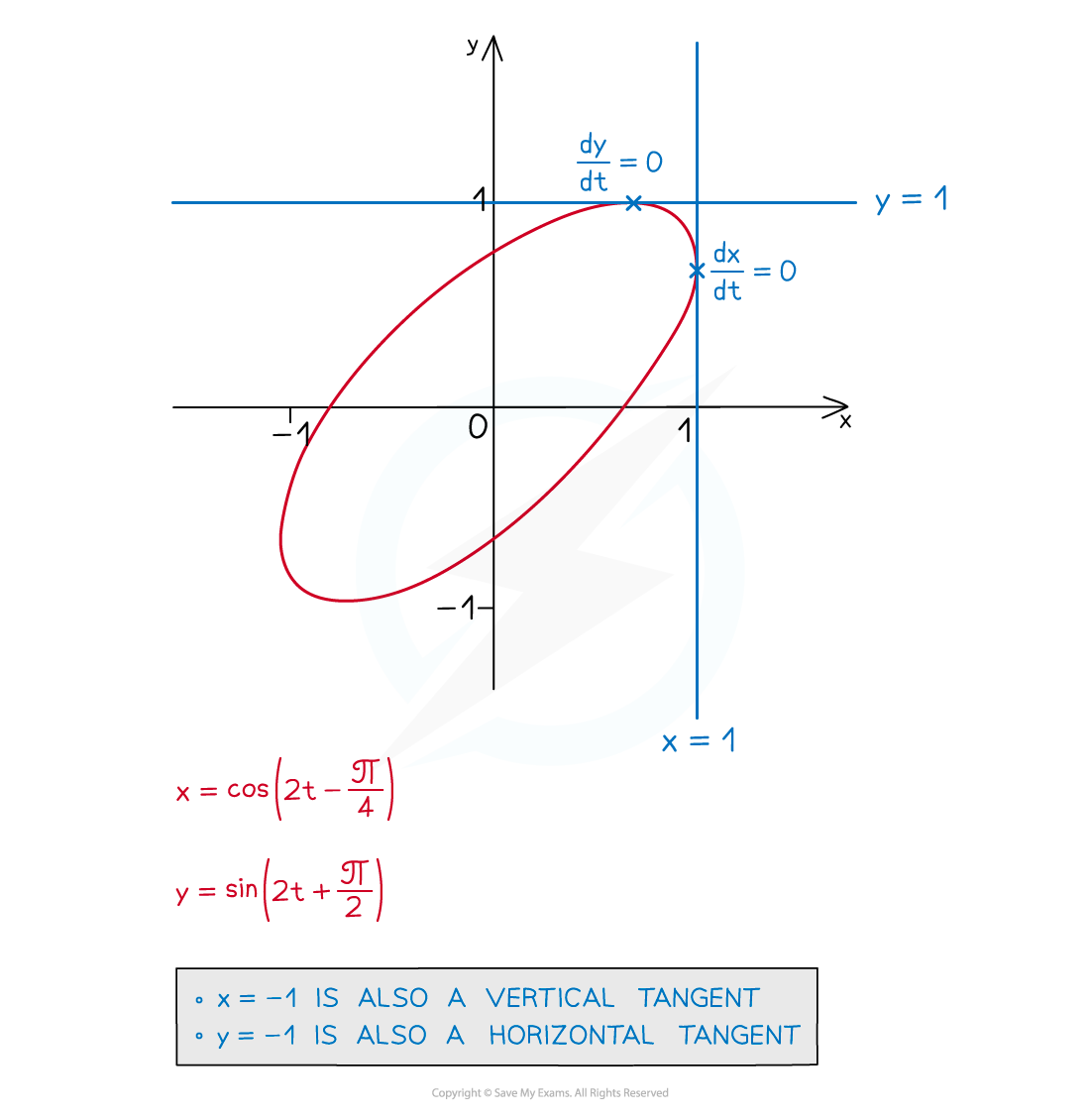
Just for fun …
Try plotting the graph from the question below using graphing software
Plenty of free online tools do this – for example Desmos and Geogebra
Try changing the domain of t to -π/3 ≤ t ≤ π/3
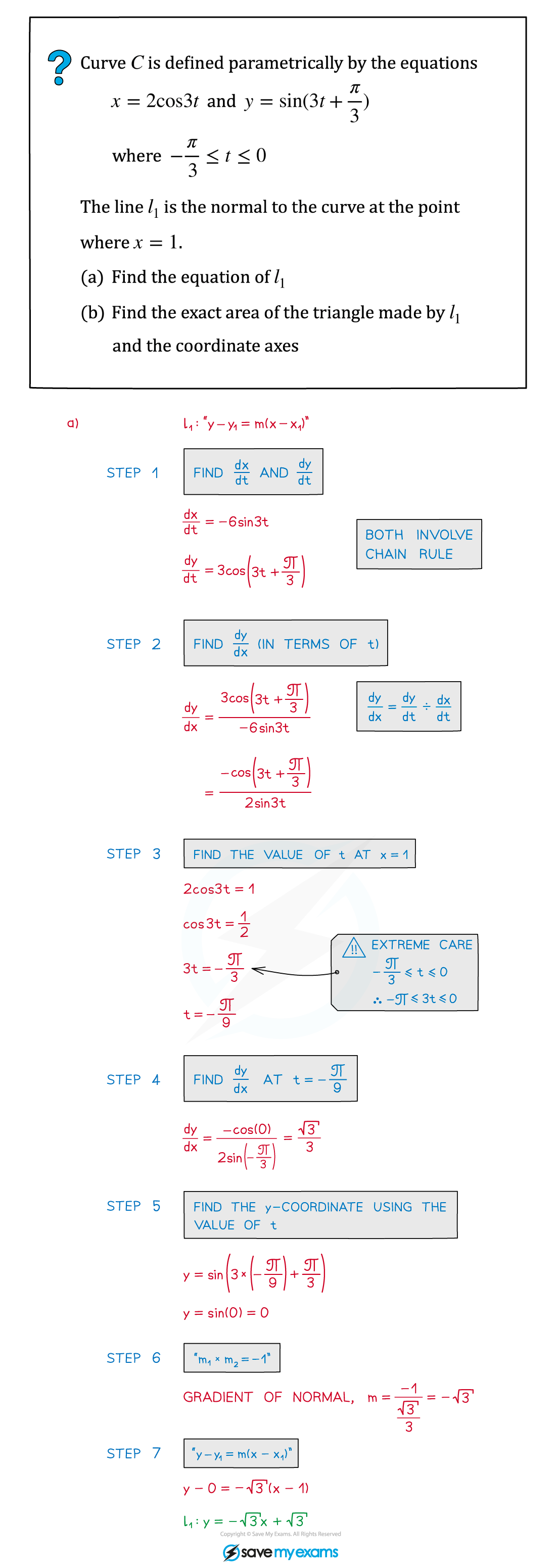
Worked Example


You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
