Solving & Interpreting Differential Equations (Edexcel A Level Maths) : Revision Note
Did this video help you?
Solving & Interpreting Differential Equations
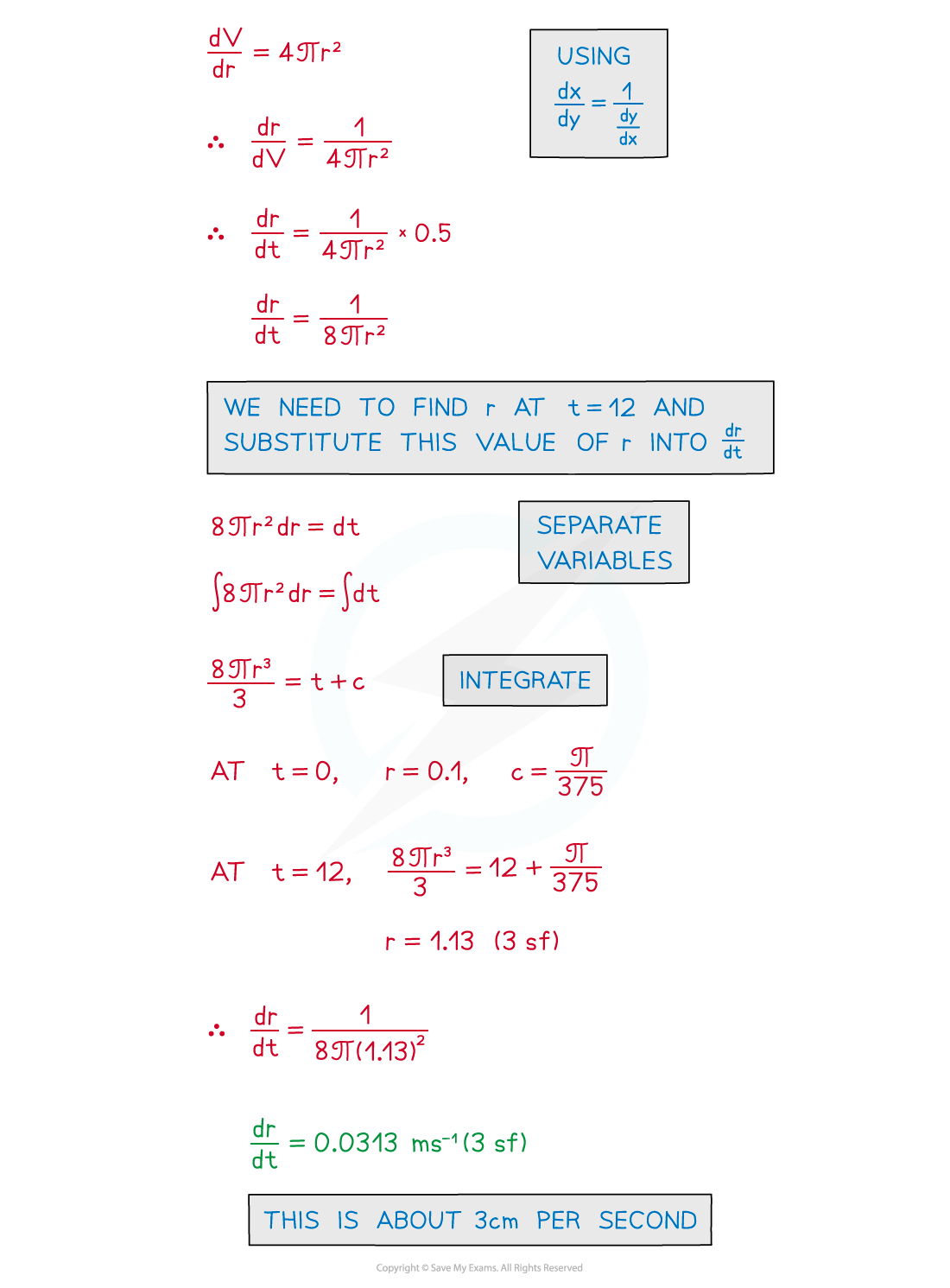
How do I solve a differential equation?
Solving differential equations uses integration!
The precise integration method will depend on the type of question (see Decision Making)
Separation of variables is highly likely to be involved
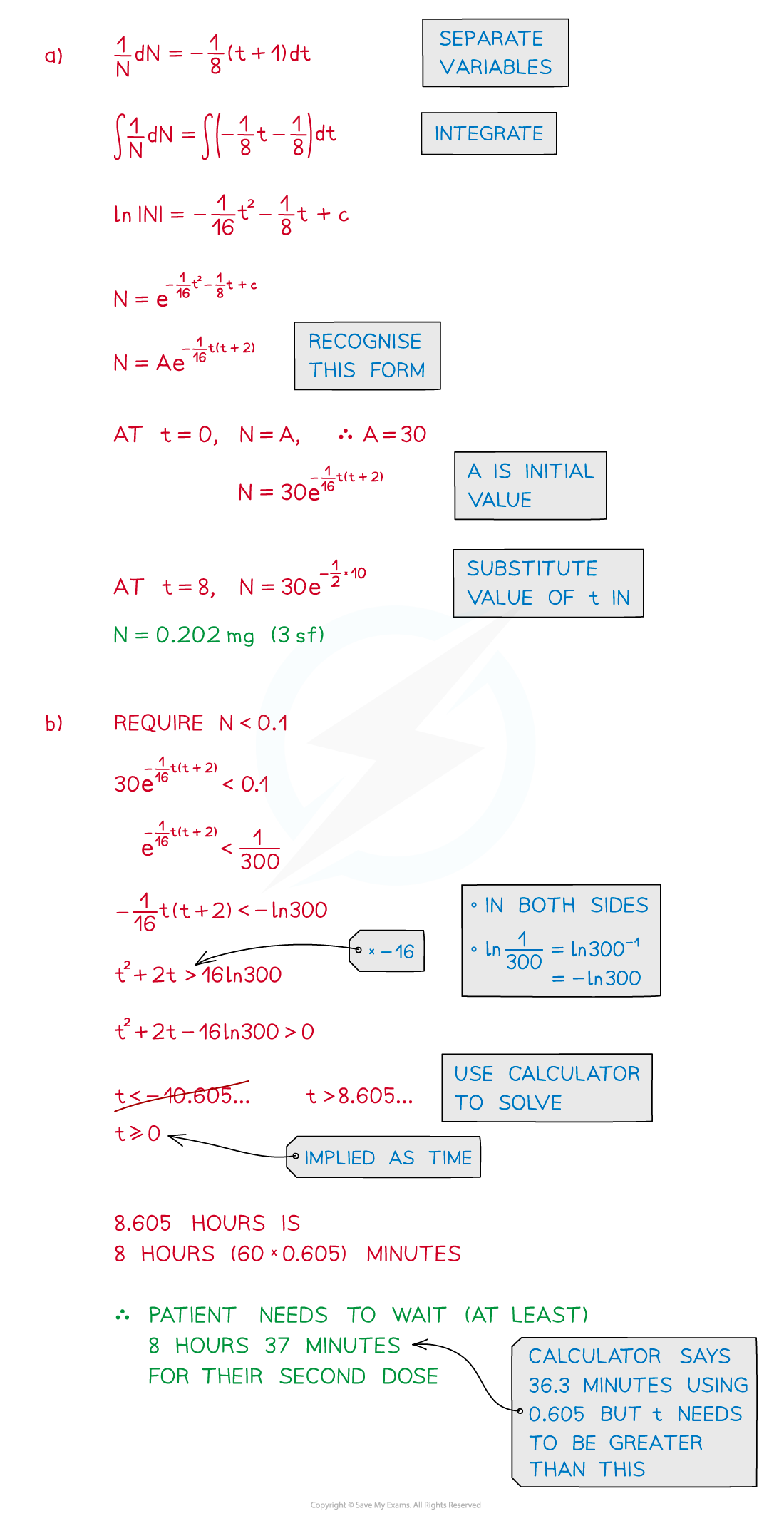
Particular solutions are usually required to Differential Equations
An initial/boundary condition is needed

Solutions can be rewritten in a format relevant to the model
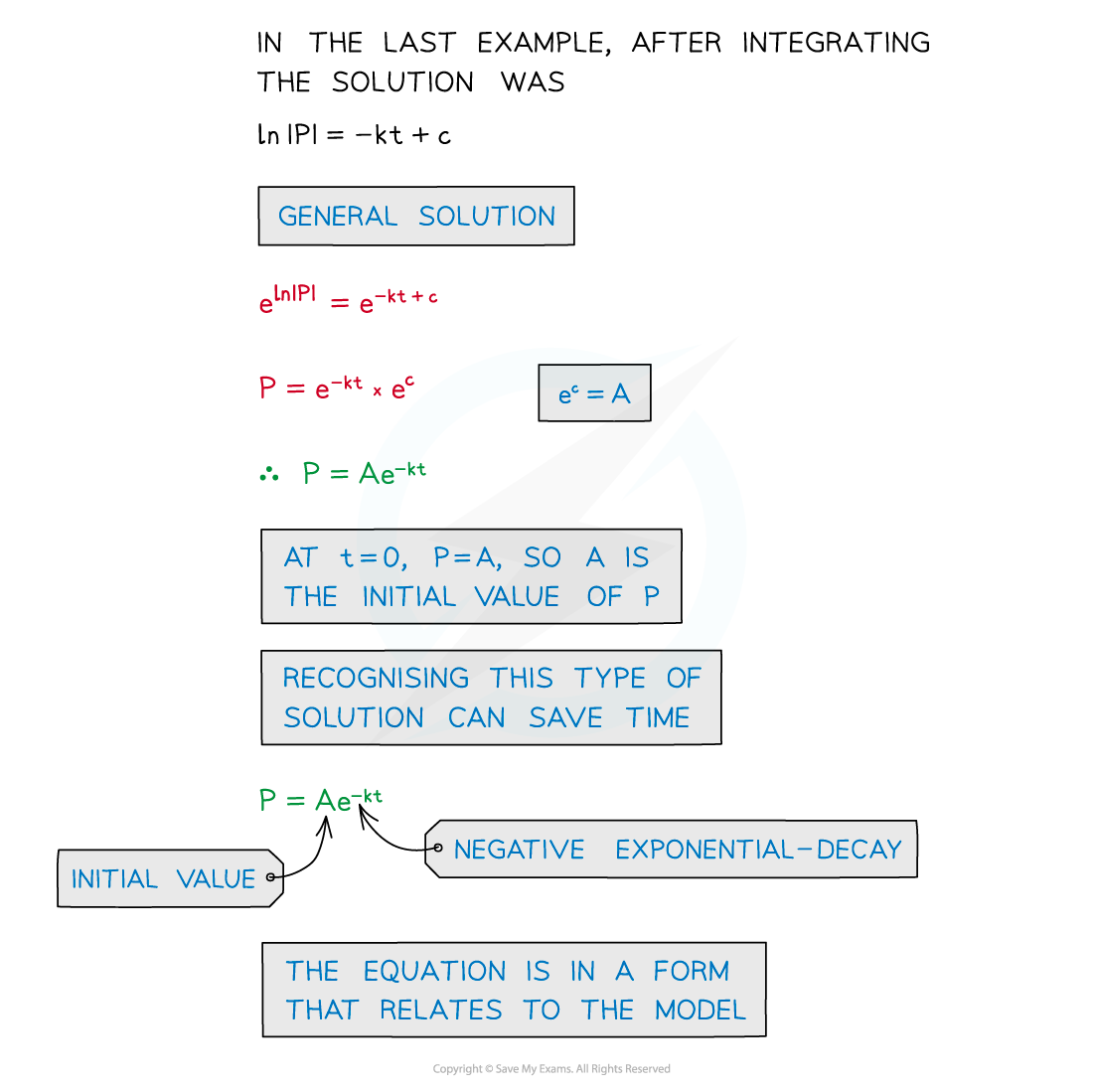
The solution can be used to make predictions at other times
Temperature after four minutes
Volume of sales after another three months
How do I use the solution to a differential equation?
Questions may ask you to interpret your solutions in the context of the problem

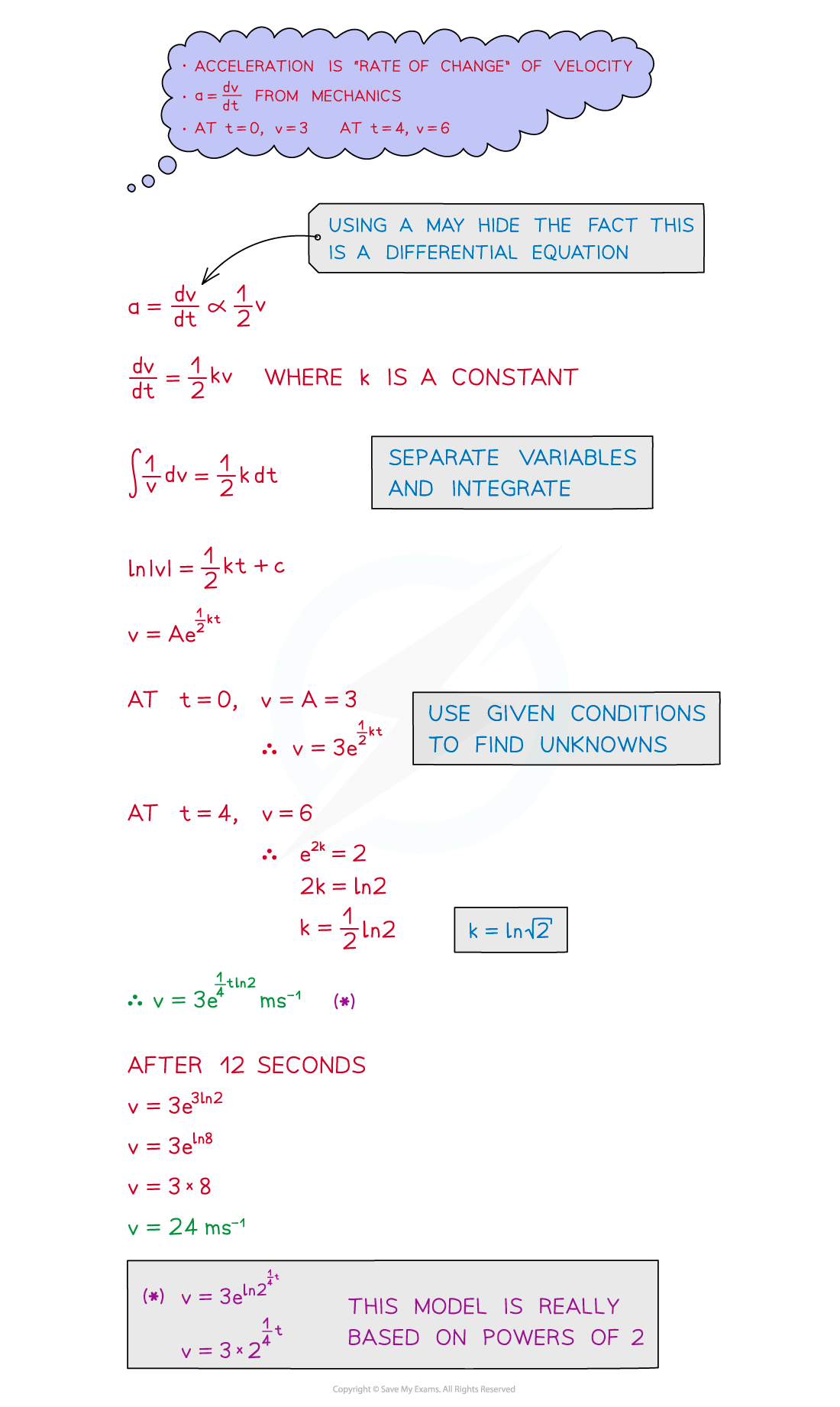
There could be links to other areas of A level maths – such as mechanics

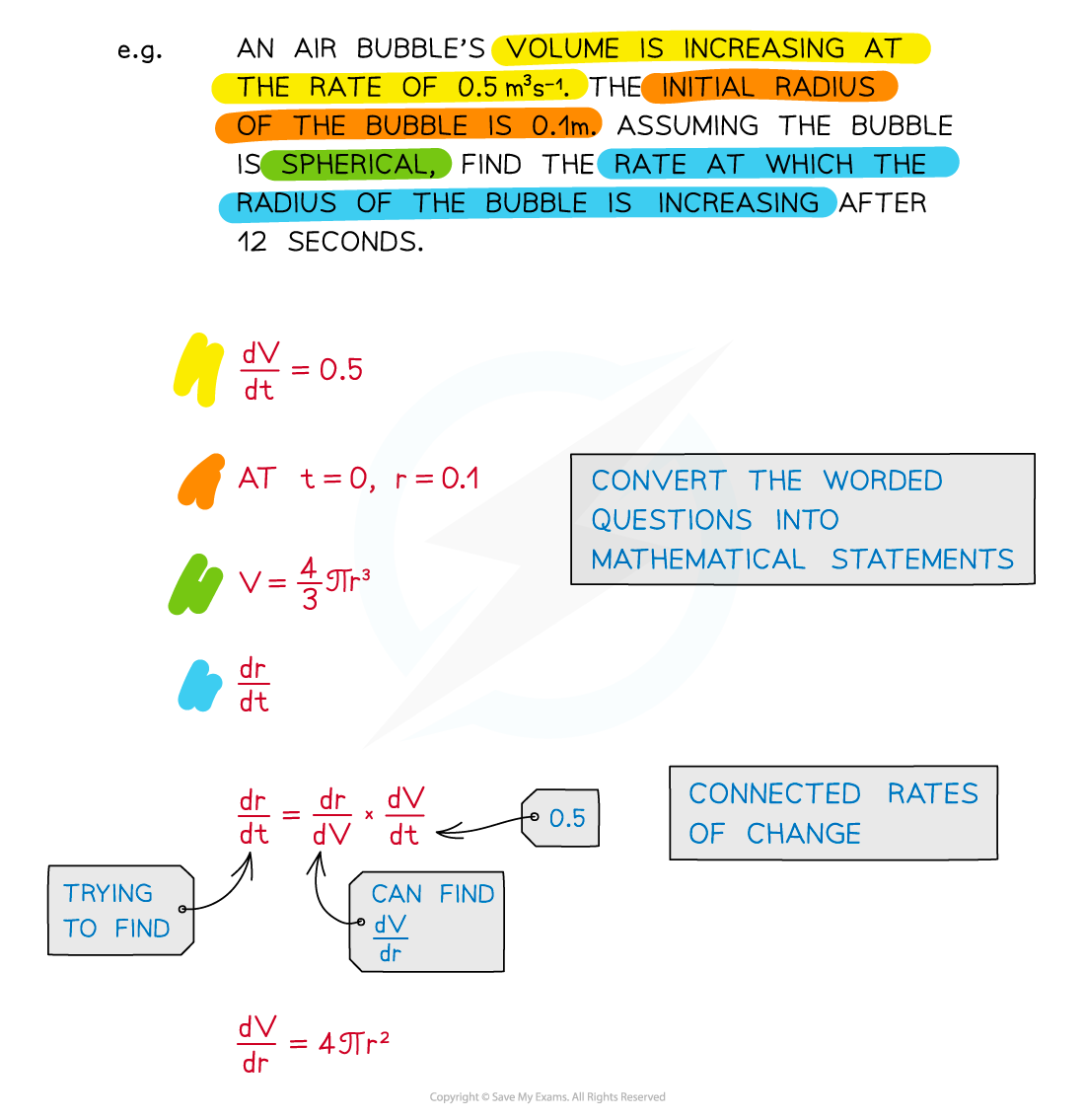
Sometimes multiple rates of change may be involved in a model or problem
See Connected Rates of Change
How do I interpret a differential equation?
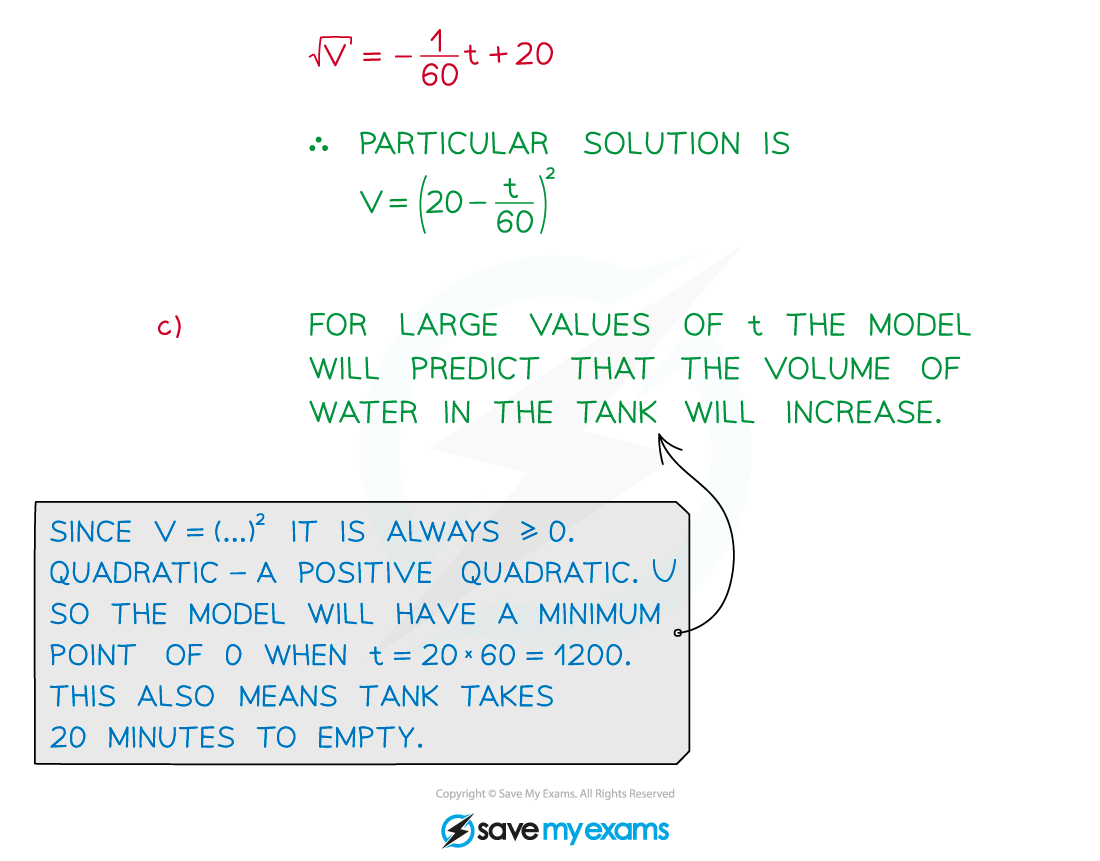
Models may not always be realistic in the long term
A population will not grow indefinitely – it will reach a natural limit
You will be expected to interpret and comment on the model

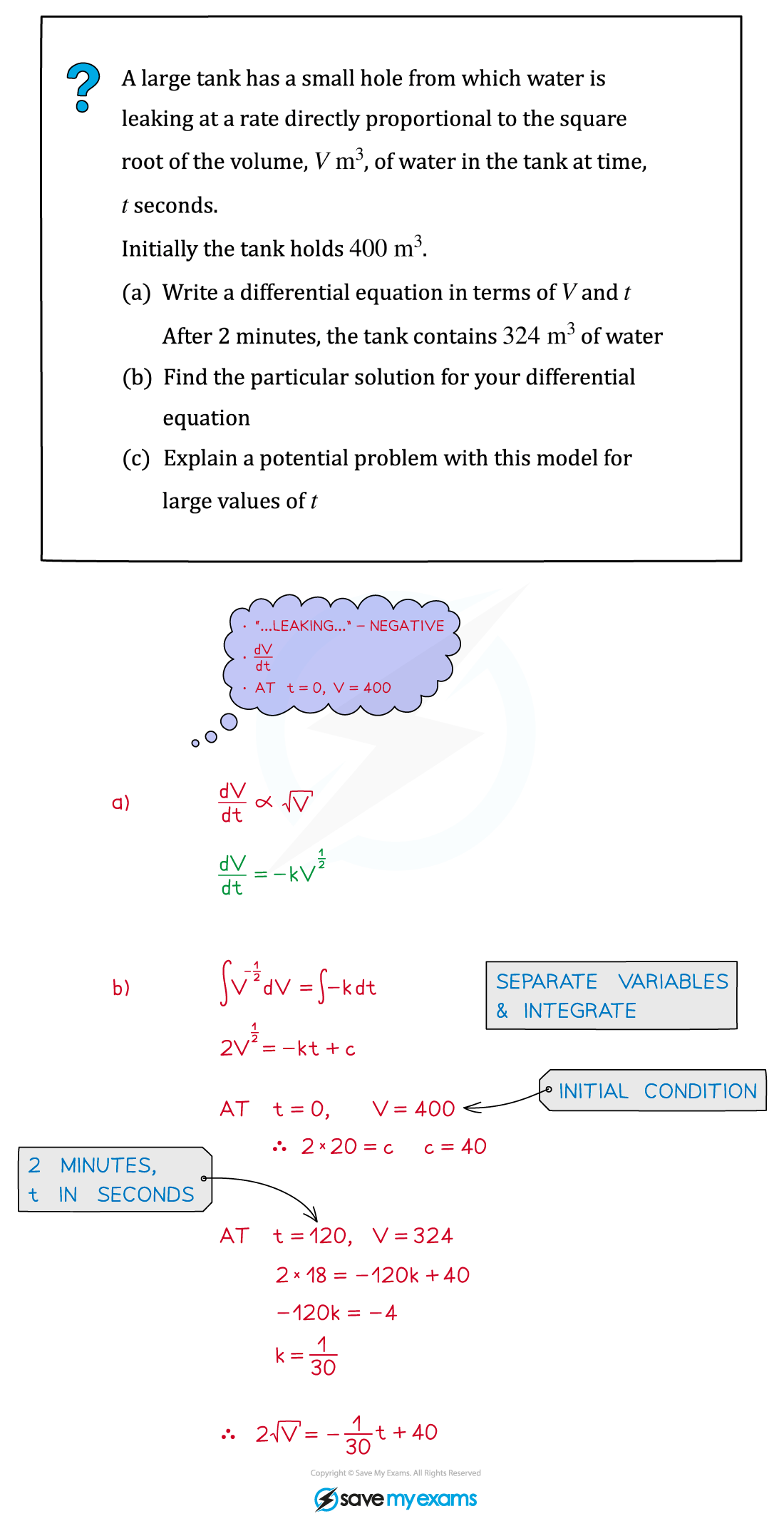
Worked Example

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
