Functions (Cambridge (CIE) A Level Maths: Pure 1): Exam Questions

State whether the following mappings are one-to-one, many-to-one, one-to-many or many-to-many.

(i)

(ii)

(iii)

(iv)

The function is defined as

Sketch the graph of giving the coordinates of any points where the graph intercepts the coordinate axes and the coordinates of the turning point.

Write down the range of

The function is defined as

Work out the range of .

If the domain of is changed to what is the range of ?

The functions and  are defined as follows

Write down the range of .

Find     

(i)

(ii)

Solve the equation  

The graph of  is shown below.

Use the graph to write down the domain and range of

Given that the point (1, 1) lies on the dotted line, write down the equation of the line.

On the diagram above sketch the graph of

The function is defined as

Show that  can be written in the form

Explain why the inverse of   does not exist and suggest an adaption to its domain so the inverse does exist.

The domain of is changed to . Find an expression for  and state its domain and range.

The functions   and  are defined as follows

Find

(i)

(ii)

Write down  and state its domain and range.

It is given

Write down the domain of the function .

Sketch the graph of stating the coordinates of any intersections with the coordinate axes and the equations of any asymptotes.

Write down the range of 

The function  is defined as

Work out the range of 

If the domain of is changed to , what is the range of ?

The functions and are defined as follows

Write down the range of .

Find

(i)

(ii)

Solve the equation 

The graph of is shown below.

(i) Use the graph to write down the domain and range of

(ii) Write down the equation of the dotted line on the graph.

 On the diagram above sketch the graph of .

The functions  and  are defined as follows

Find

(i)

(ii)

Write down and state its domain and range.

The graphs of and   are drawn on the same axes. Describe the transformation that would map one graph onto the other.

It is given

Write down the domain and range of the function

Sketch the graph of stating the coordinates of any intersections with the coordinate axes. (You do not need to give the coordinates of any turning points.)

The function is defined as

Work out the range of

If the domain of  is changed to   , what is the range of  ?

State another domain for  that would have the same effect as that in part (b).

The functions  and  are defined as follows

Write down the range of

Leaving your answers as single fractions, find

      (i)

      (ii)

Solve the equation 

The graphs of and  (dotted line) are shown in the diagram below.  has rotational symmetry about the origin and for , there is a vertical line of symmetry at 

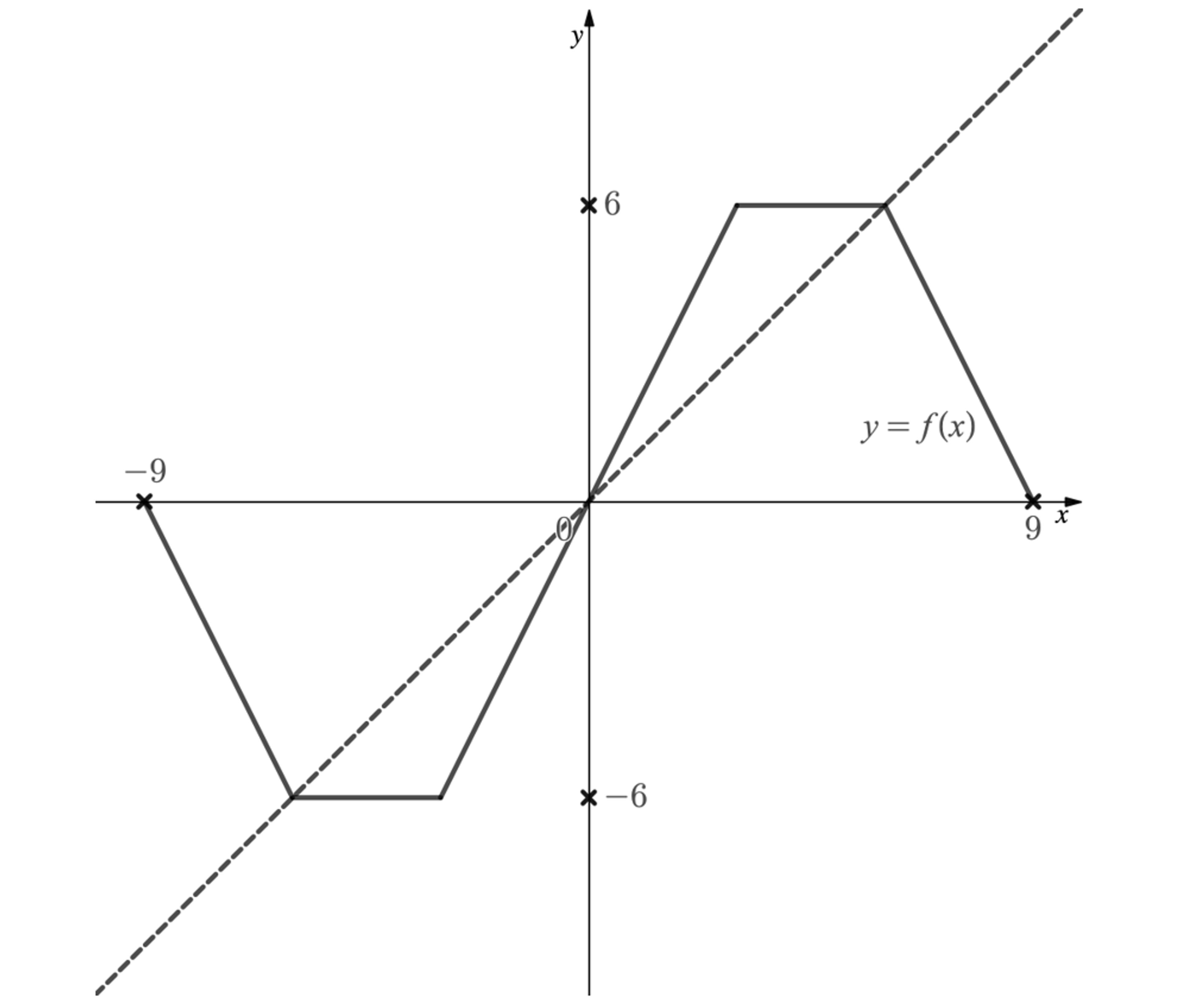
Use the graph to write down the domain and range of

On the diagram above sketch the reflection of in the line y = x and explain why this cannot be the graph of  

(i) Given that the maximum solution to is , state the restriction on the domain of such that exists.

(ii) Hence, or otherwise, write down the domain and range of .

The function  is defined as

Explain why the inverse of  does not exist.

Suggest an adaption to the domain of  so the following conditions are met:

• the inverse of  exists,

• the graph of  lies in the first quadrant only, and,

• the domain of  is as large as possible.

State the range for your adapted .

The domain of is changed to   Find an expression for  and state its domain and range.

The functions    and  are defined as follows

Find

      (i) 

      (ii) 

Write down  and state its domain and range.

The graphs of    and  are drawn on the same axes. Describe the transformation that would map one graph onto the other.

Find the coordinates of the point where the graphs of  and  meet.