Desert System Skills (AQA A Level Geography) : Revision Note
Hot Desert Skills
Short answer questions
These questions only assess knowledge (AO1) and carry 4 marks each
Four clear statements are needed (not always sentences) that answer the question and shows knowledge of the topic
Examples or details are useful but not always needed
Take no longer than 5 minutes to answer these questions
Climate graphs
Climate graphs show average rainfall and temperatures typically experienced in a particular location
Temperature is shown on a line graph, and rainfall on a bar graph
They are usually represented on the same set of axes with the months of the year along the base

Interpreting and describing climate graphs
Look at the overall shape of the graph
Is the temperature line steep or gentle?
Does it change throughout the year or look almost flat?
Look for extremes
Quote the highest and lowest temperature and rainfall and the month in which it occurs
Remember to quote units, eg celsius or millimetres
Identify the seasons when most or least rain falls
Or when the highest and lowest temperatures are experienced
Work out the temperature range by subtracting the lowest figure from the highest figure
Add the rainfall totals for each month together to work out the total annual rainfall
Worked Example
Describe the climate of Jeddah, Saudi Arabia
[4 marks]

The climate here is arid, as precipitation is 79 mm per annum [1]
Temperature range is mostly constant throughout the yea r[1]
The average annual temperature is 28.1 °C with summer high of 32.4 ‘C in August and winter low 24.6°C in January [1]
The driest months are May to Sept with zero mm of rain [1]
Wettest months are Oct to April, with a high of 26mm in Nov and a low of 2.6 mm in Feb [1]
Data response questions
All carry 6 marks and assess skills (AO3)
'Analyse' is the frequent command word
Knowledge development is not needed to explain the data and will not gain credit (just waste time)
Simple or obvious statements will gain minimum marks
Always look for patterns/trends/ranges
Identify anomalies or countertrends
Re-work the data - find percentages, mean, averages, range etc.
Use qualitative descriptive words - do not just copy from the resource
Make connections and draw relationships between different sets of data provided (compare and contrast)
Question or critique the data relationship or the data itself
Take no longer than 9 minutes to answer these questions
Data stimulus questions
Carry either 6 or 9 marks and assesses topic knowledge and ability to apply that knowledge to other situations (AO1 and AO2)
Question will usually ask for 'own knowledge' as well as a general understanding of the resource
Refer to the data provided, but also use the resource as an access route to demonstrate your own knowledge and understanding and how it applies to the wider concept of the resource
Use the same approach for data response and be prepared to make a judgement (assess)
Take no longer than 9 minutes for 6 marks or 12 minutes for 9 marks
Worked Example
Figure 4 shows a landscape in the Namib Desert in southern Africa.
Figure 4

Note: The landforms in this landscape are aligned approximately north-west to south-east and extend from between 16 km to 32 km in length, reaching heights between 60 metres to 240 metres. The sediment source is the Orange River, several kilometres away.
Using Figure 4 and your own knowledge, assess the relative importance of factors leading to the development of this landscape.
[6 marks]
Answer:
These are barchan dunes and the major factors in the development are these dunes are that they need ready supply of available sediments, which in this case is fine and coarse sand [1]. There needs to be a regular, consistent prevailing wind, which is shown in the figure running from northwest to southeast [1d].
There needs to be a smooth flat surface over which the wind can blow the sand, but also some subtle changes in the shape of the land so that sediments can collect [1]. The figure shows patches devoid of sand, but also irregularities on the surface, which would allow the sand to caught and build up [1d].
These three factors work together and that without a supply of sand from the Orange River, the barchans could not form [1]. Furthermore, a less reliable and consistent wind direction would quite quickly alter the shape of the dunes [d]. Finally, without the flat surface, sand would not be able to move and the figure shows clear evidence that sand has been completely removed from most places on the north west side of each dune [1d]. Without such flat surfaces the sand could not move so freely and the barchans could not establish such a recognisable shape [1d].
There is an equal inter-relationship between these factors which has shaped the barchans as shown in the figure. [1]
Examiner Tips and Tricks
Extended 9 mark questions are found only in the optional element and assesses AO1 and AO2.
You must show and highlight connections across the specification (synopticity) and relate it to the question.
Do not spend longer than 13 minutes and aim to write between 250 and 350 words.
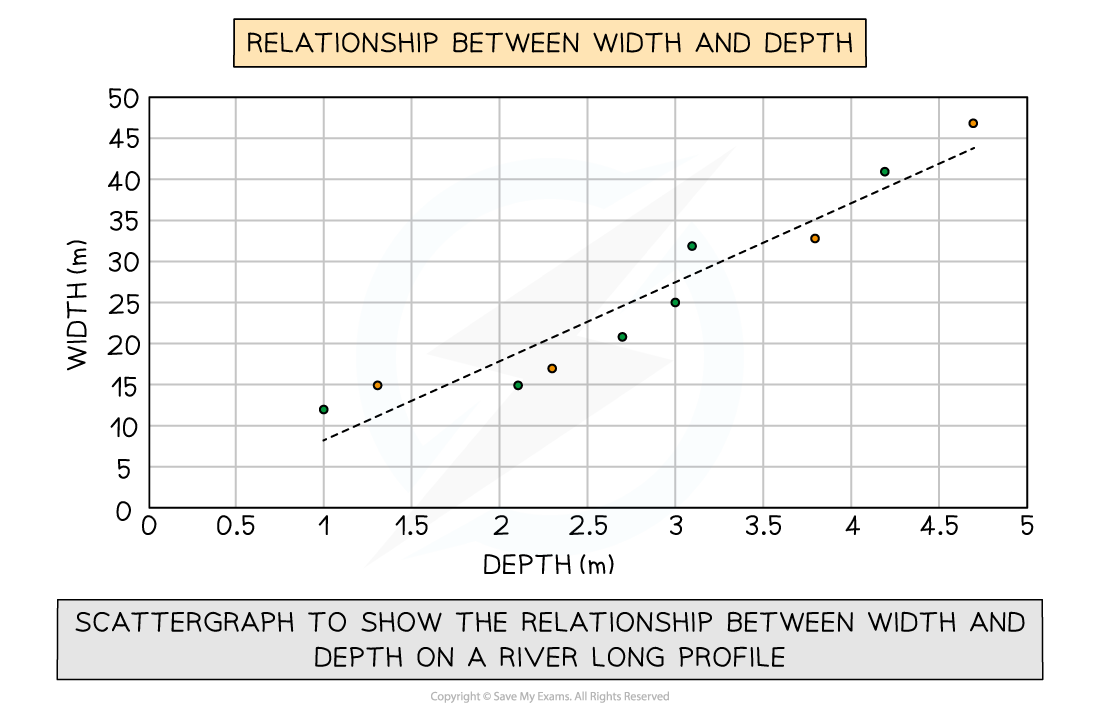
Scatter graph
Points should not be connected
The best-fit line can be added to show the relations
Used to show the relationship between two variables
In a river study, they are used to show the relationship between different river characteristics such as the relationship between the width and depth of the river channel
Strengths | Limitations |
|---|---|
Clearly shows data correlation | Data points cannot be labelled |
Shows the spread of data | Too many data points can make it difficult to read |
Makes it easy to identify anomalies and outliers | Can only show the relationship between two sets of data |
Types of correlation
Positive correlation
As one variable increases, so too does the other
The line of best fit goes from the bottom left to the top right of the graph
Negative correlation
As one variable increases the other decreases
The line of best fit goes from the top left to the bottom right of the graph
No correlation
Data points will have a scattered distribution
There is no relationship between the variables
Percentage and percentage change
To give the amount A as a percentage of sample B, divide A by B and multiply by 100
In 2020, 25 out of 360 homes in Catland were burgles. What is the percentage (to the nearest whole number) of homes burgled?
A percentage change shows by how much something has either increased or decreased
In 2021 only 21 houses were burgled. What is the percentage change in Catland?
There has been a decrease of 16% in the rate of burglaries in the Catland area
Do remember that a positive figure shows an increase but a negative is a decrease
Statistical Skills
This is the study and handling of data, which includes ways of gathering, reviewing, analysing, and drawing conclusions from data
Percentage and percentage change
To give the amount A as a percentage of sample B, divide A by B and multiply by 100
In 2020, 25 out of 360 homes in Catland were burgles. What is the percentage (to the nearest whole number) of homes burgled?
A percentage change shows by how much something has either increased or decreased
In 2021 only 21 houses were burgled. What is the percentage change in Catland?
There has been a decrease of 16% in the rate of burglaries in the Catland area
Remember that a positive figure shows an increase but a negative is a decrease
Mean, median, mode and range
Mean = average value (all the values added and divided by the number of items)
Median = middle value when ordered in size
Mode = most common value
Range = difference between the highest value and lowest value
Sample site | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
Number of pebbles | 184 | 90 | 159 | 142 | 64 | 64 | 95 |
Taking the example above to calculate:
Mean -
Median - reordering by size =
= 95 is the middle value
Mode - only 64 appears more than once
Range -
Upper, lower and interquartile range
These are the values of a quarter (25%) [lower quartile (LQ)] and three-quarters (75%) [upper (UQ)] of the ordered data
No. of shoppers | 2 | 3 | 6 | 6 | 7 | 9 | 13 | 14 | 17 | 22 | 22 |
|
|
| Lower quartile |
|
| Median |
|
| Upper quartile |
|
|
The interquartile range (IQR) is the difference between the upper (UQ) and lower quartile (LQ)
It measures the spread (dispersion) of data around the median
A large number shows the numbers are fairly spread, whereas, a small number shows the data is close to the median
UQ - LQ = IQ [
]
Standard deviation
This measures dispersion more reliably than IQR and the symbol for it is 'σ' (sigma)
The formula is
Σ means 'sum of' and
is another way of writing 'mean' and 'n' is the number of samples taken
Work out individual aspects of the formula first e.g. the mean
Sample results:
Sample site | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
Number of pebbles | 5 | 9 | 10 | 11 | 14 |
Calculate the mean -
Calculate
for each number
Square each of those values (the square of a negative number becomes positive)
Add the squared values to give
Divide the total by 'n'
Finally, find the square root
5 | 9.8 | -4.8 | 23.04 |
9 | 9.8 | -0.8 | 0.64 |
10 | 9.8 | 0.2 | 0.04 |
11 | 9.8 | 1.2 | 1.44 |
14 | 9.8 | 4.2 | 17.64 |
| |||
Numbers closely grouped around the mean shows a small deviation
A large standard deviation would show a set of numbers that were spread out
Spearman's rank correlation coefficient
A test to determine if two sets of numbers have a relationship
Not the easiest to calculate
Σ means 'sum of',
is the difference and 'n' is the number of samples taken
The formula is
Rank each number in both sets of data, with the highest number given rank 1, second highest 2 etc.
Calculate 'd' which is the difference between ranks of each group e.g. ranks for group 5 are 4 and 6; difference will be 2
Square value 'd' and calculate the total
to find
Finally, calculate the coefficient of
using the above formula
The resulting number should always be between -1 and +1
GNP ($) per capita and Life Expectancy (years)
Country | GNP | Rank | Life Expectancy | Rank | ||
|---|---|---|---|---|---|---|
1 | 15,124 | 5 | 73 | 5 | 0 | 0 |
2 | 20,535 | 4 | 72 | 6 | 2 | 4 |
3 | 10.432 | 9 | 68 | 8 | 1 | 1 |
4 | 7,050 | 11 | 62 | 11 | 0 | 0 |
5 | 22,950 | 3 | 76 | 3 | 0 | 0 |
6 | 14,800 | 6 | 75 | 4 | 2 | 4 |
7 | 23,752 | 2 | 77 | 2 | 0 | 0 |
8 | 36,875 | 1 | 79 | 1 | 0 | 0 |
9 | 5,525 | 12 | 61 | 12 | 0 | 0 |
10 | 8,678 | 10 | 66 | 9 | 1 | 1 |
11 | 12,211 | 8 | 65 | 10 | 2 | 4 |
12 | 13,500 | 7 | 70 | 7 | 0 | 0 |
| ||||||
.
rs =1 -6 ×14123 - 12 = 1- 841716 =1-0.048951 (0.05) = 0.95
(0.048951 can be rounded to 2 decimal places giving 0.05)
A positive result shows a positive correlation, where one variable increases so does the other
The closer the number is to 1, the stronger the positive correlation
A negative results shows a negative correlation, where one variable increases the other decreases
The closer the number is to -1 the stronger the negative correlation
If however, the correlation is 0 or near to 0, there is no relationship
Determining significance
Spearman's rank may show that two sets of numbers are correlated, however, it does not show how significant the link between the two values are
To check for significance; a table of critical values or a graph is needed
This looks at the probability of the links occurring by chance
A 5% or higher probability of chance is not significant evidence for a link
1% or less is a significant evidence of a link
This is the significance level of a statistical test
The degrees of freedom needs calculating - n-2
Using the example above: 12 - 2 = 10 degrees of freedom
As rs = 0.95 then the correlation has a less than 1% probability of being by chance
Therefore, there is a high significance level of a relationship between GNP and life expectancy
Spearman’s Rank Correlation Significance Table
Degrees of Freedom | 5% (0.05) | 1% (0.01) |
|---|---|---|
8 | 0.72 | 0.84 |
9 | 0.68 | 0.80 |
10 | 0.64 | 0.77 |
11 | 0.60 | 0.74 |
12 | 0.57 | 0.71 |
13 | 0.54 | 0.69 |
14 | 0.52 | 0.67 |
15 | 0.50 | 0.65 |
20 | 0.47 | 0.59 |
Examiner Tips and Tricks
Always check when making calculations what the question has asked you to do. Is it asking for units to be stated or calculate to the nearest whole number or quote to 2 decimal places.

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?

