General Algorithms (Edexcel A Level Further Maths): Revision Note
Exam code: 9FM0
Introduction to algorithms
What is an algorithm?
An algorithm is a set of precise instructions, that if strictly followed, will result in the solution to a problem
Algorithms are particularly useful for programming computers
computers can process huge amounts of data and perform millions of calculations in very short time frames
Robots would be programmed to follow an algorithm in order to complete a task
e.g. a robot vacuum cleaner or lawn mower
Algorithms can be performed by human beings too!
e.g. the recipe and cooking instructions for a cake, the instructions to build a Lego set
What does an algorithm look like?
Algorithms may be presented in a variety of ways
A list of instructions, in order, written in words/text
Pseudocode - this is a mixture of text and very basic computer commands/code
let statements, if statements and loops are common but easy enough to follow without any knowledge of a formal computer programming language
Flow charts are a visual way of presenting the steps of an algorithm
they clearly show the order of instructions and any parts of an algorithm that may need repetition
What else do I need to know about algorithms?
Some algorithms do not always provide an optimal (best) solution
but will give a solution that is sufficient for the purpose
For example, a band touring the UK may use an algorithm to find the shortest route between the different cities/venues to minimise their travelling expenses
if the algorithm is inaccurate by say, 200 miles, it is not going to make much difference overall - the band will be travelling thousands of miles in total so 200 miles is relatively little
In modern, complicated real-life situations a compromise between the speed and efficiency of an algorithm and the accuracy of the solution it provides is often needed
When using an algorithm with a small amount of data - as exam questions will do due to time restraints - it is tempting to use common sense, intuition and basic mathematical skills to 'see' the solution
to show understanding of how an algorithm works it is crucial to stay in 'robot mode'
i.e. follow the algorithm precisely and accurately without taking any 'shortcuts' (however obvious they may seem)
Examiner Tips and Tricks
Showing that you have followed an algorithm precisely includes
knowing, or using checks built into the algorithm to know, that an algorithm is complete
stating (or 'printing') any 'output' at the end if that is what an algorithm instruction requires
do not 'assume' the output is the last number in your working
Flow charts
What is a flow chart?
A flow chart is a diagrammatic way of listing the instructions to an algorithm
Flow charts lend themselves to algorithms that have
conditional instructions
e.g. Is
? If the answer is yes, the flow chart directs the user to one instruction but if the answer is no, the flow chart directs the user to a different instruction
repetitive parts or stages
What do the different shaped boxes in a flow chart mean?
Each command in a flow chart is written inside a shape - the actual shape will depend on the type of command
Ovals are used to represent the start and the end
Rectangles are used to represent instructions
Diamonds are used to represent questions

Alternative names are sometimes used for these boxes
The start and end are sometimes called termination
Question boxes are sometimes called decision boxes
The word 'print' may be used instead of 'output' for the final answer/result
How do I work with a flow chart?
Following a flow chart is generally intuitive but make sure you follow the instructions carefully
write down any values when instructed to
this will often involve completing a table of values
if there is a specific instruction to 'output' the final answer, make sure it is separate to the table
Some questions may ask for a description of what the flow chart/algorithm produces
Examiner Tips and Tricks
If a question provides a table that is to be filled in with values that change, also bear in mind that some values may not change
In such instances, only the first entry for a value may end up being entered
Not every cell in every row/column will necessarily need completing
Follow the instructions from the flow chart ('robot mode'!)
Worked Example
An algorithm is presented as a flow chart, shown below.
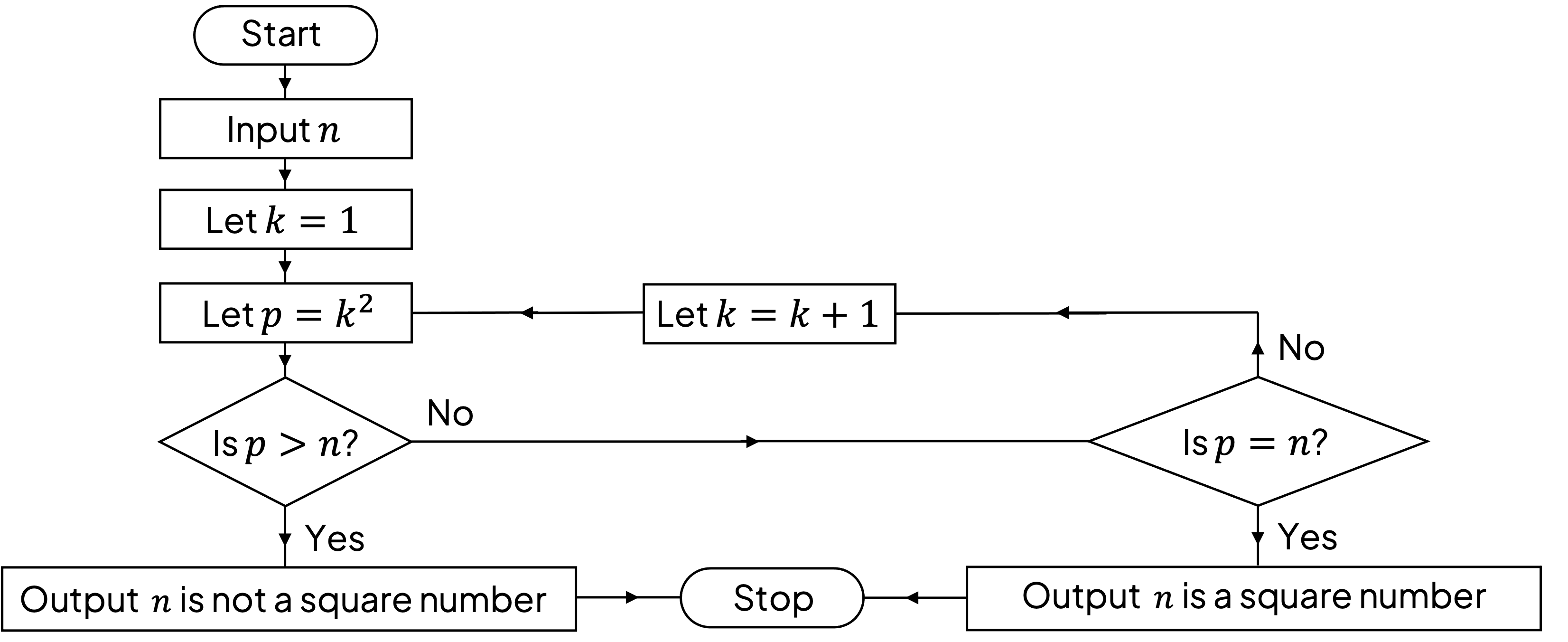
a) Describe what the algorithm achieves.
The final instructions give us a clear idea of what is going on in this case!
The algorithm works out if the input value is a square number or not
b) For the input , use the flow chart to perform the algorithm. Complete the table.
Is | Is | |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Output: |
| |||
The first instruction is to input , so fill 23 under
in the first row of the table
The next two instructions are to let and to let
, so also in the first row we can fill in 1 and 1 for
and
Is | Is | |||
23 | 1 | 1 |
|
|
|
|
|
|
|
|
|
|
|
|
The next instruction is the first question, is ; the answer is no
For the answer no, the flow chart directs us to another question, is ; the answer is no and so we can complete the top row of the table
Is | Is | |||
23 | 1 | 1 | NO | NO |
|
|
|
|
|
|
|
|
|
|
The flow chart now updates the value of ; indicate this on the second row of the table
The flow chart then takes us back round the loop of finding and testing the value of
does not get updated so only appears in the first row of the table
Is | Is | |||
23 | 1 | 1 | NO | NO |
| 2 | 4 | NO | NO |
|
|
|
|
|
Continuing to precisely follow the flow chart the table can be completed
The output needs stating at the end as per the flow chart instructions
Note how the question "is ?" does not get considered as the algorithm outputs and stops following the answer 'yes' to the question "is
?"
Is | Is | |||
23 | 1 | 1 | NO | NO |
| 2 | 4 | NO | NO |
| 3 | 9 | NO | NO |
| 4 | 16 | NO | NO |
| 5 | 25 | YES |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Output: | 23 is not a square number | |||
Pseudocode & text-based algorithms
What is pseudocode?
Pseudocode is a way of writing an algorithm that is a mixture of words and computer programming language
Pseudocode does not follow any conventions that a formal computer programming language (such as Python) would
knowledge or experience of computer programming is not expected
What commands are used in pseudocode?
Commands given in pseudocode are intuitive to follow
Examples include
'Input ...' - the value(s)/data that the algorithm needs to be told
'Let ..." - assign or update a value to a variable
'If ...' - a conditional statement, the outcome of which will lead to different parts of the algorithm
'Int ...' - the integer part of a value
'While ...' - whilst the condition that follows is true, keep doing
'Output ...' or 'Print ...' - usually at the end of an algorithm this instruction essentially means 'write down the final answer' !
How do I work with an algorithm in pseudocode?
To show an algorithm in pseudocode has been followed precisely, the result of each command is usually jotted down
this may be in the form of a table
some values may be changed or updated during the algorithm
Ignore any commands that do not apply
e.g. in an if statement
Zeller's algorithm is given in pseudocode below
This finds the day of the week for any date in the Gregorian calendar (1582 onwards)
This version of the algorithm assumes that days will be inputted as 1-31, months 1-12 (rather than words) and years are four digits
The algorithm may give inaccurate results or 'crash' if unexpected values are input
Try using the algorithm to find the day of the week 30th February 2024 falls on
No such date exists, but 29th February 2024 is a Thursday - does the algorithm give the answer Friday?

Zeller's algorithm is most commonly used to find which day of the week on which a person was born using their date of birth
There are many variations of Zeller's algorithm, some are more complicated than others!
What are text-based algorithms?
Text-based algorithms refer to instructions that are given in sentences
Each instruction may be labelled with 1, 2, 3, and so on
Just like in many of our Save My Exams Revision Notes!
Step 1 ..., Step 2 ..., etc
The following text-based algorithm is for a very basic single player dice game
The aim of the game is to minimise the number of rolls of the dice needed to reach 'Stop'

Order of an algorithm
What is the order of an algorithm?
The order of an algorithm refers to its complexity
The complexity of an algorithm will depend on
the number of steps/instructions involved
the amount of 'input' data
A well constructed algorithm will be both accurate and efficient
The order of an algorithm is usually determined by the maximum number of steps an algorithm involves
For example, an algorithm that finds a particular item in a list would, at most, search every item on that list
the number of steps involved is a function of the number of items on the list
the algorithm would be of linear order
Quadratic order would mean the number of steps involved is a function of the square of the size of the input data
Cubic order would be a function of the cube of the size of the input data
How is the order of an algorithm described?
The order of an algorithm is described by a mathematical function
linear, quadratic and cubic are the most common
square roots, logarithms, exponentials, etc
Two different algorithms may both be of quadratic order but still take differing amount of times to complete
this is because the exact form of the quadratic functions may differ
e.g. For an input of size
, one of the algorithms may have the number of steps
but the other
both are quadratic functions but for the same value of
they take different values
How do I find the order of an algorithm?
In simple cases the order of an algorithm can be determined by considering the maximum number of steps involved
the order is determined by considering the worst case scenario
an algorithm finding an item in a list would, at most, search every item in the list
the algorithm is therefore of linear order
In many cases - particularly where the order is not easily determined, it will be given
The order of an algorithm can be used to find an approximate time of completion
The time will only be an approximation as
only the order (not the exact function) is being used
the order is determined by the maximum number of steps involved (the worst case scenario)
How do I find (an estimate for) the time an algorithm will take to complete using its order?
The time it takes an algorithm to complete is estimated using proportionality
Doubling the size of the input data to an algorithm of linear order would increase the approximate time of completion 2 times
Doubling for quadratic order would increase the approximate time of completion
times
Doubling for cubic order would increase the approximate time of completion
times
The same use of proportion applies to less common orders too
for an algorithm of order
, doubling the size of the input data would increase the approximate time of completion
times
e.g. if an algorithm takes 5 seconds to process an input of size 20, then the algorithm will take approximately
seconds to process an input of size 80
Depending on the nature of an algorithm, the use of the letter
may take different meanings
the 'input size'
may refer to the number of data items or it could be the actual size of the input
e.g. in a sorting algorithm
may be the number of items to be sorted but in an algorithm to determine if a number is prime,
may be the number being tested
when referring to the order of an algorithm,
may be the scale by which the input size has increased
e.g. in an algorithm of quadratic order, increasing the input size by
, will approximately increase the time the algorithm takes to complete by
Examiner Tips and Tricks
The words order and complexity are often used interchangeably
quadratic order and quadratic complexity are the same thing
Worked Example
An algorithm for sorting a list of values into ascending order has order
. A computer running the algorithm takes 0.12 seconds to apply the algorithm to a list of 3000 values.
Estimate the time it would take the computer to apply the algorithm to a list of 60 000 values.
It takes 0.12 seconds for an algorithm of order
Divide the time by the order and then multiply it by the order of an algorithm for a list with 60 000 items
An estimate of the time the computer would take to apply the algorithm to 60 000 values is 3.30 seconds ( 3 s.f.)

Unlock more, it's free!
Did this page help you?