Coupled First Order Linear Equations (Edexcel A Level Further Maths) : Revision Note
Coupled First Order Linear Equations
What are coupled first order linear differential equations?
Coupled first order linear differential equations are a pair of simultaneous differential equations of the form
a, b, c and d are real constants
f(t) and g(t) are functions of t
In your exam these functions will usually be either zero or else simply equal to a constant
The equations are described as ‘coupled’ because the rate of change of each of the variables depends not only on the variable itself but also on the other variable
Systems of coupled differential equations often occur in modelling contexts where two variables are expected to interact
For example x may refer to the size of a population of prey animals, and y to the size of a population of predators
We would expect the rate of change of the prey animal population to depend on the number of prey animals there are to reproduce, but also on the number of predator animals eating the prey animals
Similarly we would expect the rate of change of the predator animal population to depend on the number of predator animals there are to reproduce, but also on the number of prey animals there are for the predators to eat
How do I solve coupled first order linear differential equations?
You can solve coupled systems by turning them into an uncoupled second order differential equation that you know how to solve
For example, consider the coupled system
STEP 1: Rearrange one of the equations to make the variable that is not in the derivative the subject
We can rearrange the first equation to get
STEP 2: Differentiate both sides of the equation from Step 1 with respect to t
Differentiating gives
STEP 3: Substitute the equations from Steps 1 and 2 into the coupled differential equation you didn’t use in Step 1
Substituting into the second equation gives
The result is a second order differential equation in only one of the variables
STEP 4: Solve the second order differential equation resulting from Step 3
Using the standard solution methods for second order differential equations gives the solution
STEP 5: To find the solution for the other variable, substitute the solution from Step 4 along with its derivative into the equation from Step 1
Differentiate
to get
Then substituting into the Step 1 equation gives
STEP 6: If the question provides initial or boundary conditions you may use these to find the values of A and B, and then go on to interpret your solutions in the context of whatever situation the coupled system of differential equations may be modelling
Worked Example
In the following system of coupled differential equations, the variable x represents the population size of a species of prey fish in a particular region of ocean, while the variable y represents the population size of a species of predator fish in the same region.
a) Show that .
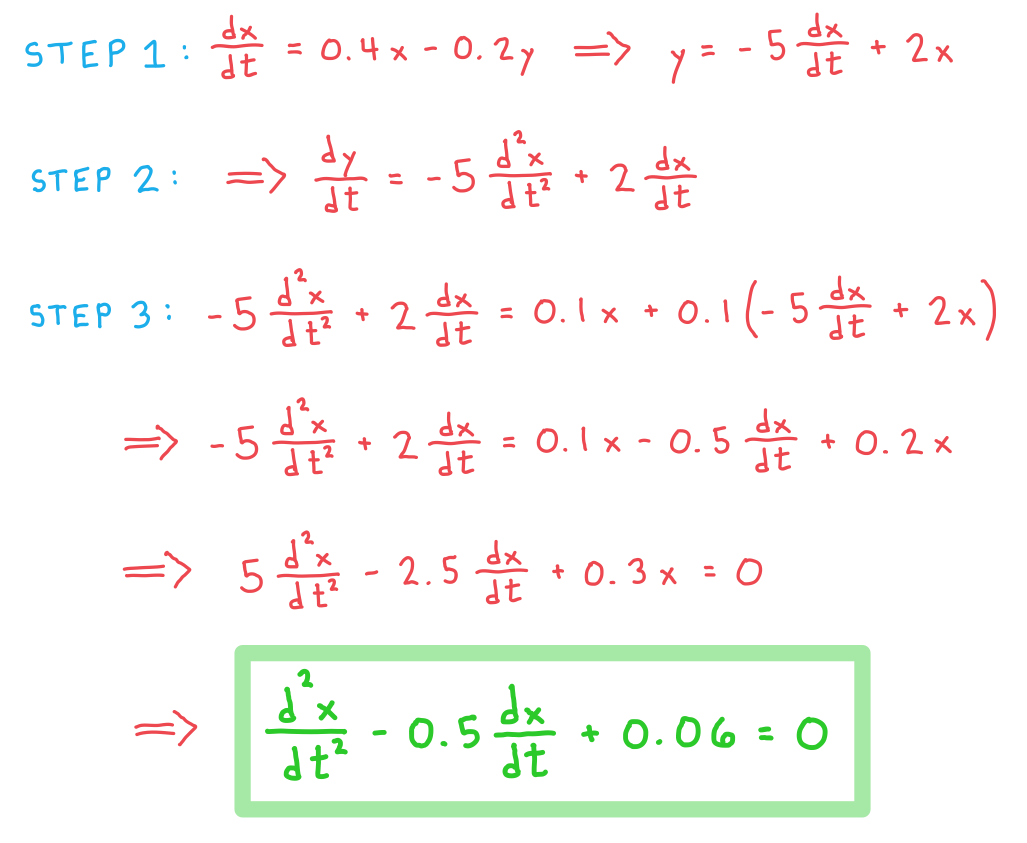
b) Find the general solution for the number of prey fish in the region at time t.
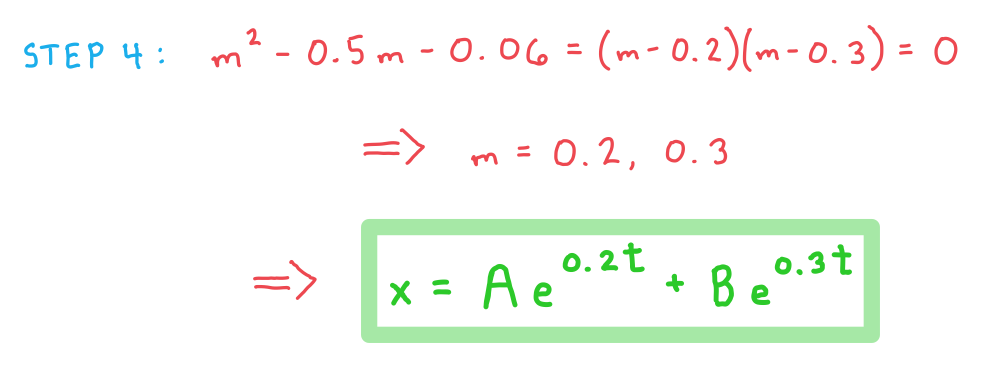
c) Find the general solution for the number of predator fish in the region at time t.

d) Given that there are initially 6000 prey fish and 3500 predator fish in the region, find the number of each species that the model predicts for time t = 3.

e) Comment on the suitability of the model.


You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?
