Introduction to Complex Numbers (Edexcel A Level Further Maths) : Revision Note
Cartesian Form of Complex Numbers
Complex numbers are a set of numbers which contain both a real part and an imaginary part. The set of complex numbers is denoted as .
What is an imaginary number?
Up until now, when we have encountered an equation such as
we would have stated that there are “no real solutions” as the solutions are
which are not real numbers
To solve this issue, mathematicians have defined one of the square roots of negative one as
; an imaginary number
We can use the rules for manipulating surds to manipulate imaginary numbers.
We can do this by rewriting surds to be a multiple of
using the fact that
What is a complex number?
Complex numbers have both a real part and an imaginary part
For example:
The real part is 3 and the imaginary part is 4
Note that the imaginary part does not include the '
'
Complex numbers are often denoted by
and we can refer to the real and imaginary parts respectively using
and
In general:
This is the Cartesian form of z
It is important to note that two complex numbers are equal if, and only if, both the real and imaginary parts are identical.
For example,
and
are not equal
Examiner Tips and Tricks
Be careful in your notation of complex and imaginary numbers.
For example:
could also be written as
, but if you wrote
this could easily be confused with
.
Worked Example
a) Solve the equation
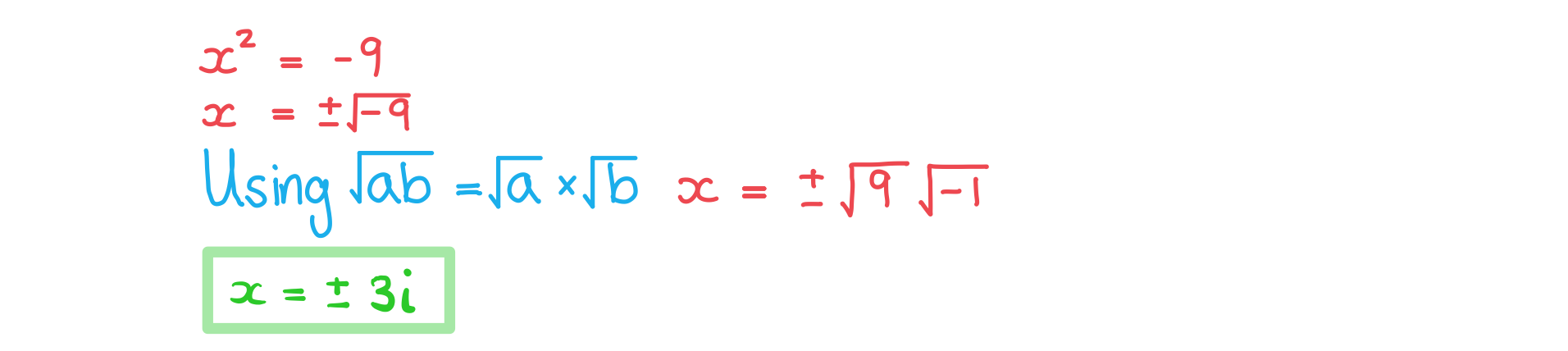
b) Solve the equation , giving your answers in Cartesian form.

Operations with Complex Numbers
How do I add and subtract complex numbers?
When adding and subtracting complex numbers, simplify the real and imaginary parts separately
Just like you would when collecting like terms in algebra and surds, or dealing with different components in vectors
Complex numbers can also be multiplied by a constant in the same way as algebraic expressions:
How do I multiply complex numbers?
The most important thing to bear in mind when multiplying complex numbers is that
We can still apply our usual rules for multiplying algebraic terms:
Sometimes when a question describes multiple complex numbers, the notation
is used to represent each complex number
How do I deal with higher powers of i?
Because
this can lead to some interesting results for higher powers of i
We can use this same approach of using i2 to deal with much higher powers
Just remember that -1 raised to an even power is 1 and raised to an odd power is -1
Examiner Tips and Tricks
Most calculators used at A-Level can work with complex numbers and you can use these to check your working.
You should still show your full working though to ensure you get all marks though.
Worked Example
a) Simplify the expression .

b) Given two complex numbers and
, find
.

Complex Conjugation & Division
When dividing complex numbers, we can use the complex conjugate to make the denominator a real number, which makes carrying out the division much easier.
What is a complex conjugate?
For a given complex number
, the complex conjugate of
is denoted as
, where
If
then
You will find that:
is always real because
For example:
is always imaginary because
For example:
is always real because
(as
)
For example:
How do I divide complex numbers?
When we divide complex numbers, we can express the calculation in the form of a fraction, and then start by multiplying the top and bottom by the conjugate of the denominator:
This ensures we are multiplying by 1; so not affecting the overall value
This gives us a real number as the denominator because we have a complex number multiplied by its conjugate (
)
This process is very similar to “rationalising the denominator” with surds which you may have studied at GCSE
Examiner Tips and Tricks
We can speed up the process for finding
by using the basic pattern of
We can apply this to complex numbers:
(using the fact that
)
So
multiplied by its conjugate would be
Worked Example
Find the value of .


You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?
