Coupled First Order Linear Equations

What are coupled first order linear differential equations?

Coupled first order linear differential equations are a pair of simultaneous differential equations of the form

$\begin{array}{rcl} \frac{d x}{d t} & = & a x + b y + f (t) \\ \frac{d y}{d t} & = & c x + d y + g (t) \end{array}$

a, b, c and d are real constants
f(t) and g(t) are functions of t

In your exam these functions will usually be either zero or else simply equal to a constant

The equations are described as ‘coupled’ because the rate of change of each of the variables depends not only on the variable itself but also on the other variable

Systems of coupled differential equations often occur in modelling contexts where two variables are expected to interact

For example x may refer to the size of a population of prey animals, and y to the size of a population of predators

We would expect the rate of change of the prey animal population to depend on the number of prey animals there are to reproduce, but also on the number of predator animals eating the prey animals
Similarly we would expect the rate of change of the predator animal population to depend on the number of predator animals there are to reproduce, but also on the number of prey animals there are for the predators to eat

How do I solve coupled first order linear differential equations?

You can solve coupled systems by turning them into an uncoupled second order differential equation that you know how to solve

For example, consider the coupled system
$\frac{d x}{d t} = 0.6 x + 2 y \frac{d y}{d t} = 3.12 x + 0.4 y$

STEP 1: Rearrange one of the equations to make the variable that is not in the derivative the subject
- We can rearrange the first equation to get $y = 0.5 \frac{d x}{d t} - 0.3 x$
STEP 2: Differentiate both sides of the equation from Step 1 with respect to t
- Differentiating gives $\frac{d y}{d t} = 0.5 \frac{d^{2} x}{d t^{2}} - 0.3 \frac{d x}{d t}$
STEP 3: Substitute the equations from Steps 1 and 2 into the coupled differential equation you didn’t use in Step 1
- Substituting into the second equation gives

$0.5 \frac{d^{2} x}{d t^{2}} - 0.3 \frac{d x}{d t} = 3.12 x + 0.4 (0.5 \frac{d x}{d t} - 0.3 x) \frac{d^{2} x}{d t^{2}} - \frac{d x}{d t} - 6 x = 0$

- The result is a second order differential equation in only one of the variables

STEP 4: Solve the second order differential equation resulting from Step 3
- Using the standard solution methods for second order differential equations gives the solution

$x = A e^{3 t} + B e^{- 2 t}$

STEP 5: To find the solution for the other variable, substitute the solution from Step 4 along with its derivative into the equation from Step 1
- Differentiate $x = A e^{3 t} + B e^{- 2 t}$ to get $\frac{d x}{d t} = 3 A e^{3 t} - 2 B e^{- 2 t}$
- Then substituting into the Step 1 equation gives

$y = 0.5 (3 A e^{3 t} - 2 B e^{- 2 t}) - 0.3 (A e^{3 t} + B e^{- 2 t}) y = 1.2 A e^{3 t} - 1.3 B e^{- 2 t}$

STEP 6: If the question provides initial or boundary conditions you may use these to find the values of A and B, and then go on to interpret your solutions in the context of whatever situation the coupled system of differential equations may be modelling

Worked example

In the following system of coupled differential equations, the variable x represents the population size of a species of prey fish in a particular region of ocean, while the variable y represents the population size of a species of predator fish in the same region.

$\frac{d x}{d t} = 0.4 x - 0.2 y \frac{d y}{d t} = 0.1 x + 0.1 y$

Show that

\frac{d^{2} x}{d t^{2}} - 0.5 \frac{d x}{d t} + 0.06 x = 0

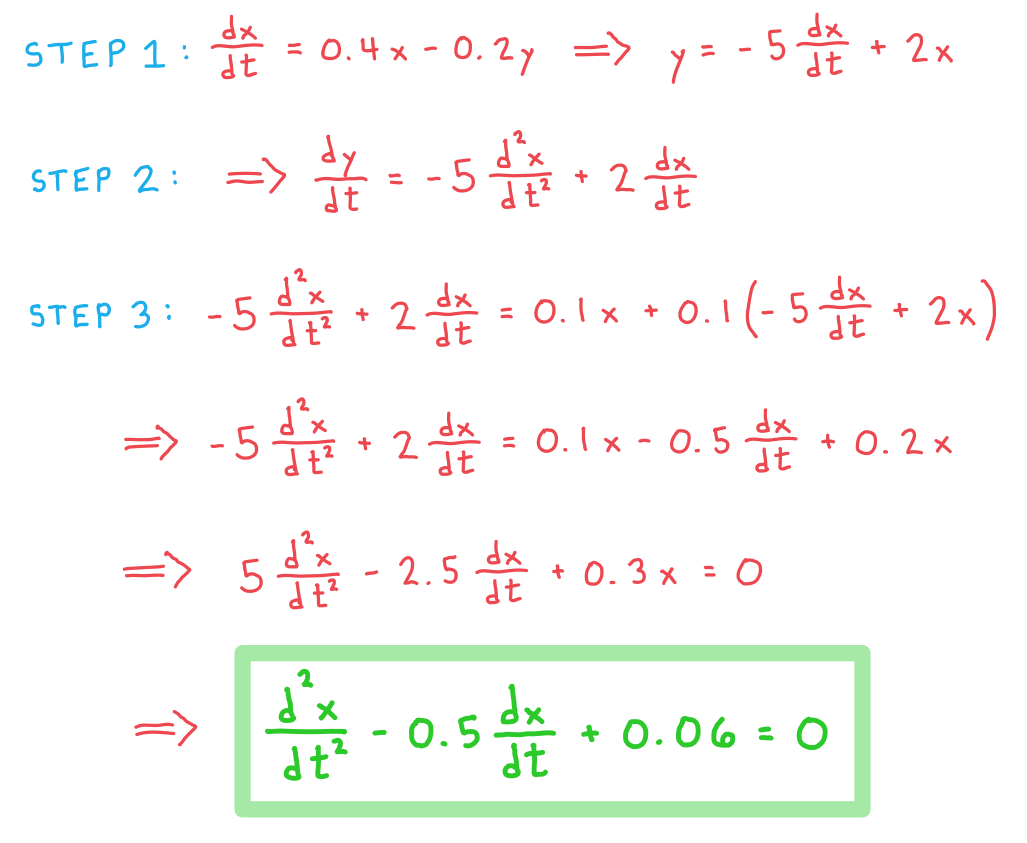
8-2-2-coupled-1st-order-linear-eqns-a-we-solution

Find the general solution for the number of prey fish in the region at time t.

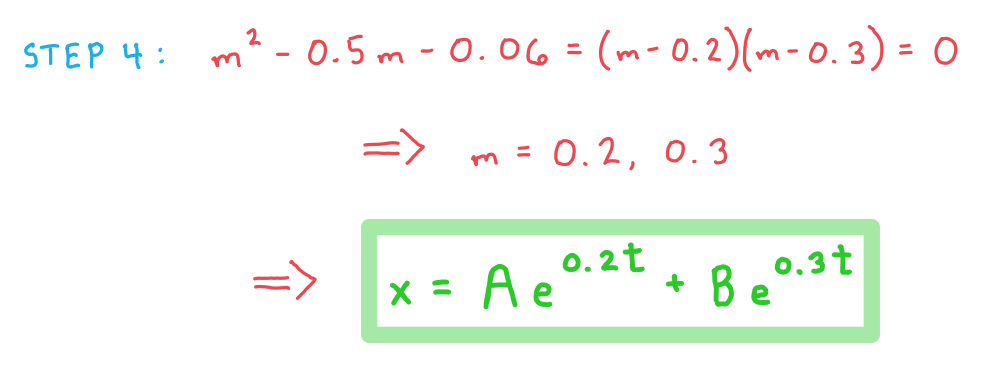
8-2-2-coupled-1st-order-linear-eqns-b-we-solution

Find the general solution for the number of predator fish in the region at time t.

8-2-2-coupled-1st-order-linear-eqns-c-we-solution

Given that there are initially 6000 prey fish and 3500 predator fish in the region, find the number of each species that the model predicts for time t = 3.

8-2-2-coupled-1st-order-linear-eqns-d-we-solution

Comment on the suitability of the model.

8-2-2-coupled-1st-order-linear-eqns-e-we-solution

Coupled First Order Linear Equations (Edexcel A Level Further Maths: Core Pure)

Revision Note