Improper Integrals

What are improper integrals?

An improper integral is a definite integral where one or both of the limits is either:
- Positive or minus infinity
- A point where the function is undefined
  - Consider the graph of $y = \frac{1}{\sqrt{x}}$
  - It is undefined at the point x = 0
  - The integral of $y = \frac{1}{\sqrt{x}}$ with a limit of zero would be an improper integral
Examples include:
- $\int_{0}^{5} \frac{1}{\sqrt[3]{x}} d x = \lim_{a \to 0} \int_{a}^{5} \frac{1}{\sqrt[3]{x}} d x$
- $\int_{1}^{\infty} \frac{1}{x^{3}} d x = \lim_{b \to \infty} \int_{1}^{b} \frac{1}{x^{3}} d x$

6-1-5-improper-integrals-diagram-1

How do we find the value of an improper integral?

Use algebra to replace the limit which cannot be found with a variable
- E.g. let the undefined limit of zero be a or the infinite limit be b
Evaluate the integral and substitute your chosen variable into the expression
Consider what will happen to your answer as the value of your chosen variable tends towards the limit
- E.g. what happens as a gets closer to zero or as b gets closer to infinity?
Your final answer will be the value you get if you substitute this into your answer
- E.g. as a tends to zero a² tends to zero and so this part of your solution will be zero
It is useful to remember as a tends to infinity then $\frac{1}{a}$ tends to 0

Examiner Tip

Be careful if a limit of your integral is zero, always check to see if the function is defined at zero and if not treat it as an improper integral.
Infinite limits will always be treated as improper integrals.

Worked example

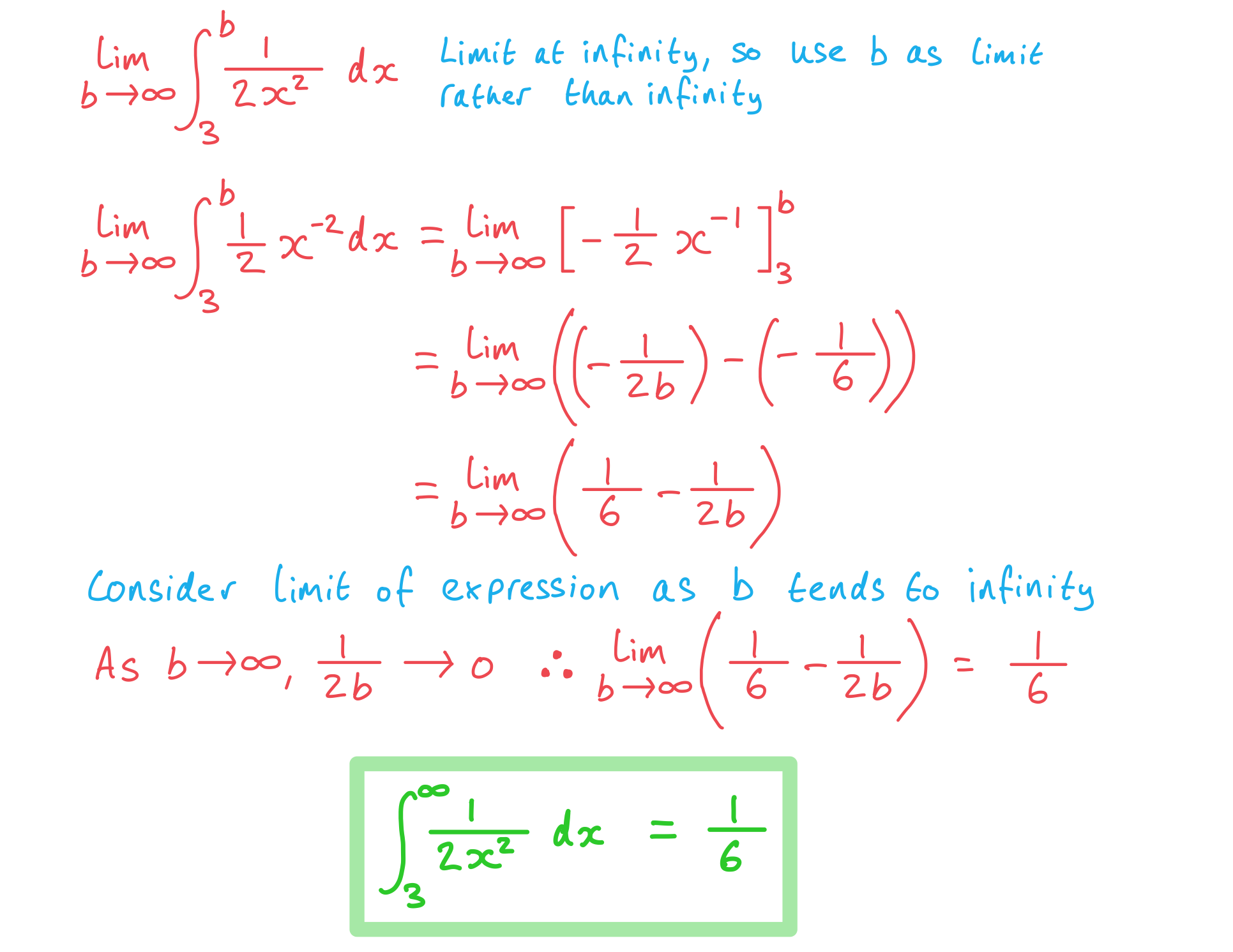
Find the following improper integrals, give your answers as exact values,

$\int_{0}^{3} \frac{1}{2 \sqrt{x}} d x$

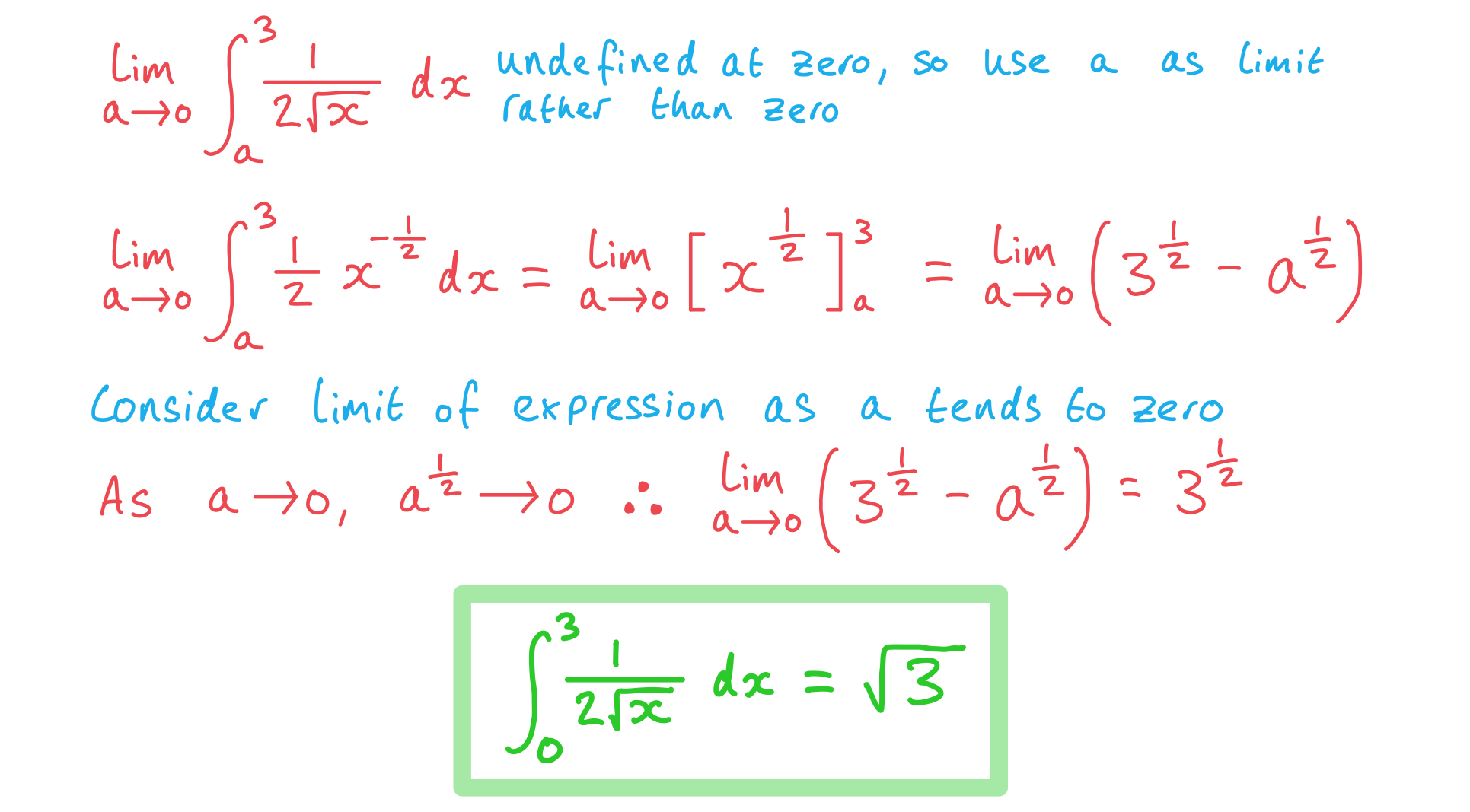
5-2-1-edx-a-fm-we1a-soltn

\int_{3}^{\infty} \frac{1}{2 x^{2}} d x

5-2-1-edx-a-fm-we1b-soltn

Improper Integrals (Edexcel A Level Further Maths: Core Pure)

Revision Note

What are improper integrals?

How do we find the value of an improper integral?

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

1. Complex Numbers

1.1 Complex Numbers & Argand Diagrams

1.1.1 Introduction to Complex Numbers

1.1.2 Solving Equations with Complex Roots

1.1.3 Modulus & Argument

1.1.4 Modulus-Argument Form

1.1.5 Loci in Argand Diagrams

1.1.6 Regions in Argand Diagrams

1.2 Exponential Form & de Moivre's Theorem

1.2.1 Exponential Form

1.2.2 de Moivre's Theorem

1.2.3 Applications of de Moivre's Theorem

1.2.4 Roots of Complex Numbers

2. Matrices

2.1 Properties of Matrices

2.1.1 Introduction to Matrices

2.1.2 Determinants of Matrices

2.1.3 Inverses of Matrices

2.2 Transformations using Matrices

2.2.1 Transformations using a Matrix

2.2.2 Geometric Transformations with Matrices

2.2.3 Invariant Points & Lines

3. Further Algebra & Functions

3.1 Roots of Polynomials

3.1.1 Roots of Polynomials

3.1.2 Linear Transformations of Roots

3.2 Series

3.2.1 Sums of Integers, Squares & Cubes

3.2.2 Method of Differences

3.3 Maclaurin Series

3.3.1 Maclaurin Series

4. Hyperbolic Functions

4.1 Hyperbolic Functions

4.1.1 Hyperbolic Functions & Graphs

4.1.2 Logarithmic Forms of Inverse Hyperbolic Functions

4.1.3 Hyperbolic Identities & Equations

4.1.4 Differentiating & Integrating Hyperbolic Functions

5. Further Calculus

5.1 Volumes of Revolution

5.1.1 Volumes of Revolution

5.1.2 Modelling with Volumes of Revolution

5.2 Methods in Calculus

5.2.1 Improper Integrals

5.2.2 Mean Value of a Function

5.2.3 Integrating with Partial Fractions

5.2.4 Calculus involving Inverse Trig

5.2.5 Integration by Substitution

6. Further Vectors

6.1 Vector Lines

6.1.1 Equations of Lines in 3D

6.1.2 Pairs of Lines in 3D

6.1.3 Angle between Lines

6.1.4 Shortest Distances - Lines

6.2 Vector Planes

6.2.1 Equations of planes

6.2.2 Combinations of Lines & Planes

6.2.3 Combinations of Planes

6.2.4 Shortest Distances - Planes

7. Polar Coordinates

7.1 Polar Coordinates

7.1.1 Polar Coordinates

7.1.2 Calculus with Polar Coordinates

8. Differential Equations

8.1 First Order Differential Equations

8.1.1 Intro to Differential Equations

8.1.2 Solving First Order Differential Equations

8.1.3 Modelling using First Order Differential Equations

8.2 Second Order Differential Equations

8.2.1 Solving Second Order Differential Equations

8.2.2 Coupled First Order Linear Equations

8.3 Simple Harmonic Motion

8.3.1 Simple Harmonic Motion

8.3.2 Damped or Forced Harmonic Motion