Volumes of Revolution (Edexcel A Level Further Maths) : Revision Note

Volumes of revolution around the x-axis

What is a volume of revolution around the x-axis? 

• A solid of revolution is formed when an area bounded by a function  (and other boundary equations) is rotated 360° around the x-axis

• A volume of revolution is the volume of this solid formed

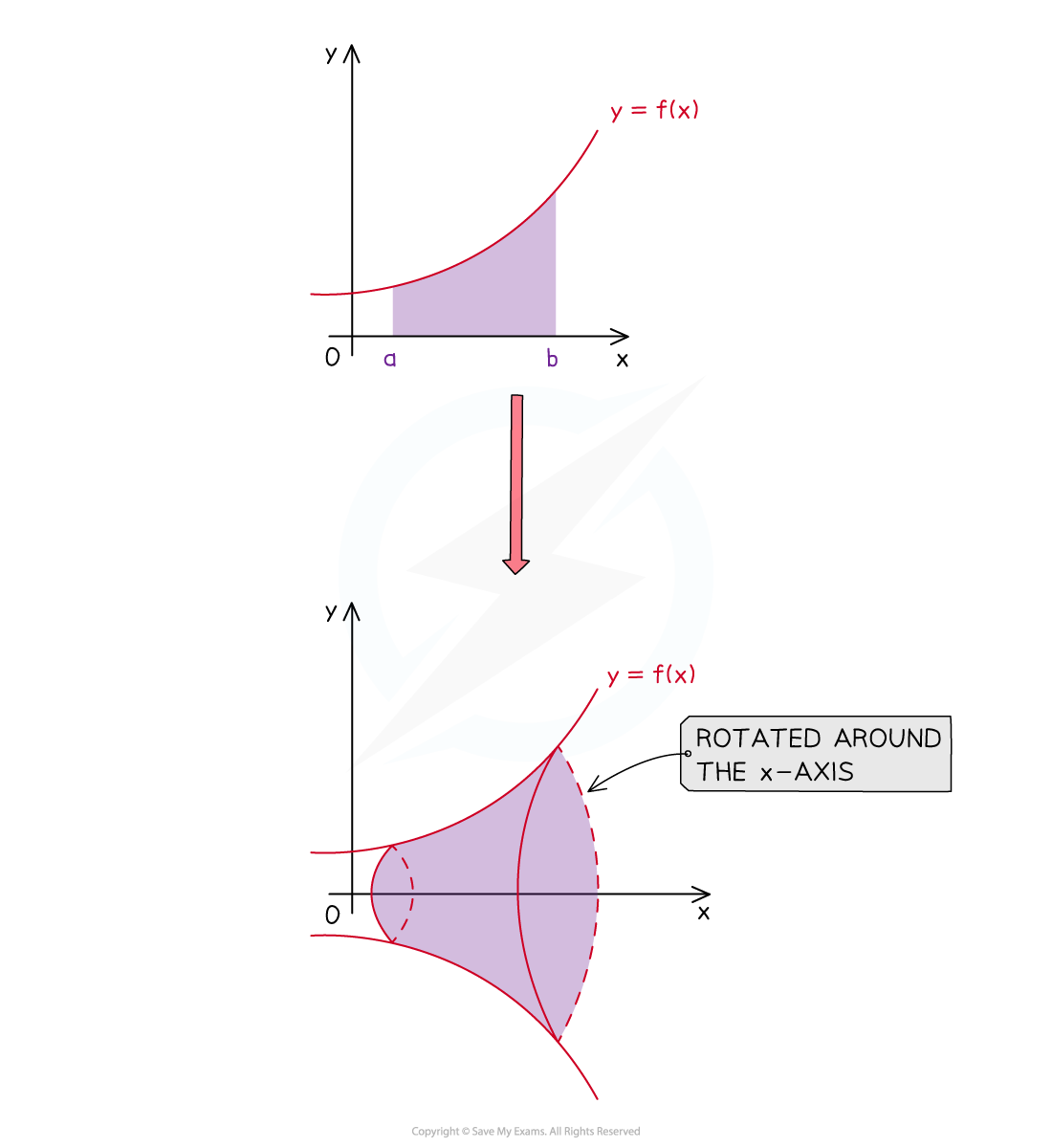
Example of a solid of revolution that is formed by rotating the area bounded by the function , the lines  and   and the -axis about the -axis

How do I find the volume of revolution around the x-axis? 

• To find the volume of revolution created when the area bounded by the function , the lines  and , and the x-axis is rotated 360° about the x-axis use the formula

• The formula may look complicated or confusing at first due to the y and dx

  • remember that y is a function of x

  • once the expression for y is substituted in, everything will be in terms of x

• π is a constant so you may see this written either inside or outside the integral

• This is not given in the formulae booklet

  • The formulae booklet does list the volume formulae for some common 3D solids – it may be possible to use these depending on what information about the solid is available

Where does the formula for the volume of revolution come from?

• When you integrate to find the area under a curve you can see the formula by splitting the area into rectangles with small widths

  • The same method works for volumes

• Split the volume into cylinders with small widths

  • The radius will be the y value

  • The width will be a small interval along the x-axis δx

• The volume can be approximated by the sum of the volumes of these cylinders

• The limit as δx goes to zero can be found by integration - just like with areas

How do I solve problems involving volumes of revolution around the x-axis? 

• Visualising the solid created is helpful

  • Try sketching some functions and their solids of revolution to help

•  STEP 1 Square y            

  • Do this first without worrying about π or the integration and limits

• STEP 2 Identify the limits a and b (which could come from a graph)

• STEP 3 Use the formula by evaluating the integral and multiplying by π

  • The answer may be required in exact form (leave in terms of π)

    • If not, round to three significant figures (unless told otherwise)

• Trickier questions may give you the volume and ask for the value of an unknown constant elsewhere in the problem

Volumes of revolution around the y-axis

What is a volume of revolution around the y-axis? 

• A solid of revolution is formed when an area bounded by a function  (and other boundary equations) is rotated 360° around the y-axis

• A volume of revolution is the volume of this solid formed

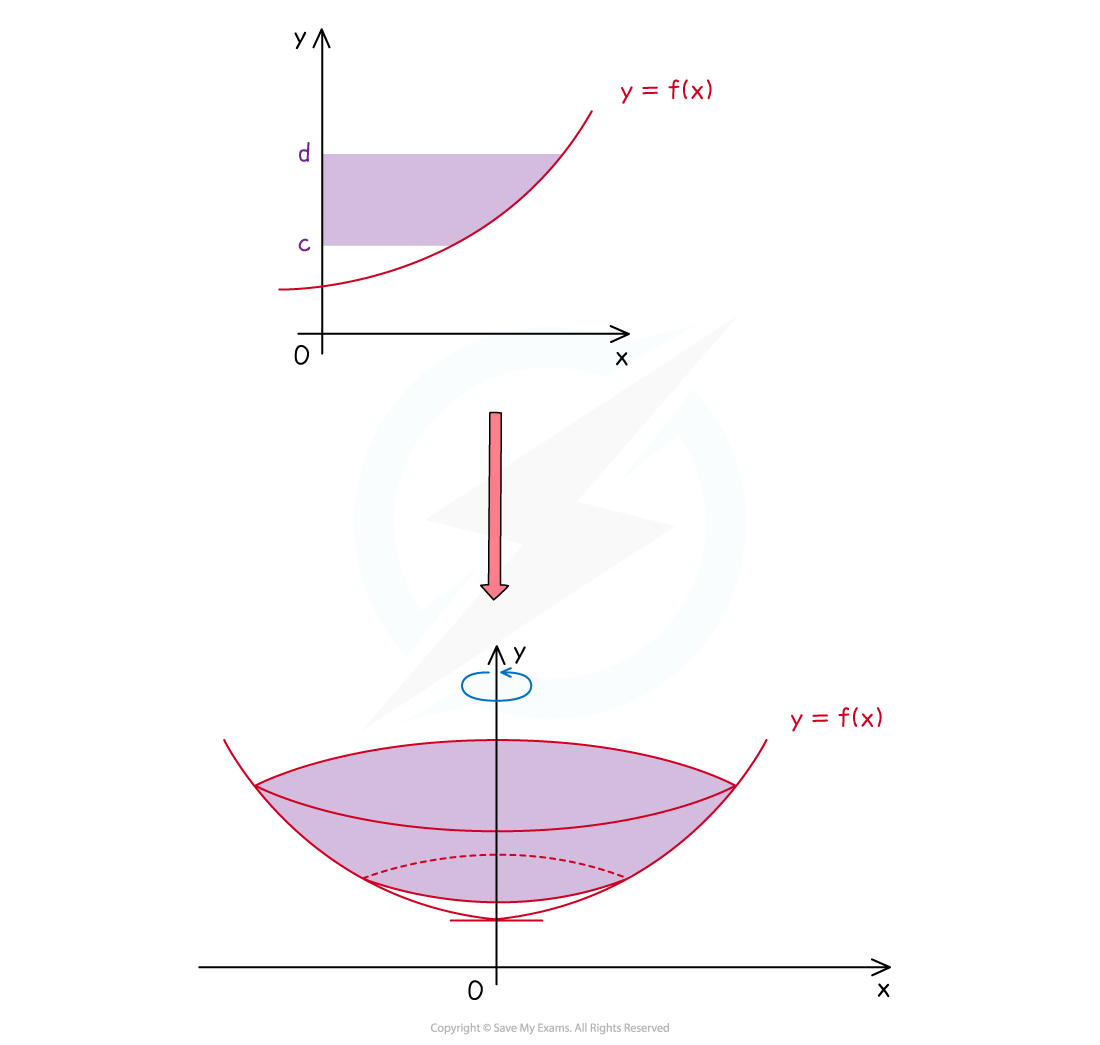
Example of a solid of revolution that is formed by rotating the area bounded by the function , the lines and  and the -axis about the -axis

How do I find the volume of revolution around the y-axis? 

• To find the volume of revolution created when the area bounded by the function , the lines  and , and the y-axis is rotated 360° about the y-axis use the formula

• Note that although the function may be given in the form  it will first need rewriting in the form  

• This is not given in the formulae booklet

How do I solve problems involving volumes of revolution around the y-axis? 

• Visualising the solid created is helpful

  • Try sketching some functions and their solids of revolution to help 

• STEP 1 Rearrange  into the form  (if necessary)

  • This is finding the inverse function 

• STEP 2 Square x

  • Do this first without worrying about π or the integration and limits

• STEP 3 Identify the limits c and d (which could come from a graph)

• STEP 4 Use the formula by evaluating the integral and multiplying by π

  • The answer may be required in exact form (leave in terms of π)

    • If not, round to three significant figures (unless told otherwise) 

• Trickier questions may give you the volume and ask for the value of an unknown constant elsewhere in the problem

Volumes of Revolution using Parametric Equations

What is parametric volumes of revolution? 

• Solids of revolution are formed by rotating functions about the x-axis or the y-axis

• Here though, rather than given y in terms of x, both x and y are given in terms of a parameter, t

  • 

  •  

  • Depending on the nature of the functions f and g it may not be convenient or possible to find y in terms of x

How do I find volumes of revolution when x and y are given parametrically?

• The aim is to replace everything in the ‘original’ integral so that it is in terms of t

• For the ‘original’ integral or  and parametric equations given in the form  and use the following process

• STEP 1: Find dx or dy in terms of t and dt

  •  or 

• STEP 2: If necessary, change the limits from x values or y values to t values using

  • or 

  • or 

• STEP 3: Square y or x

  •  or 

  • Do this separately to avoid confusing when putting the integral together

• STEP 4: Set up the integral, so everything is now in terms of t, simplify where possible and evaluate the integral to find the volume of revolution

(if around x-axis) or (if around y-axis)