Hyperbolic Identities & Equations

Are there identities linking the hyperbolic functions to the circular trig functions?

Yes - these can be seen using de Moivre's Theorem to write
- $\cos x = \frac{1}{2} (e^{i x} + e^{- i x})$
- $\sin x = \frac{1}{2 i} (e^{i x} - e^{- i x})$
Compare these with the definitions for the hyperbolic functions
- $\cosh x = \frac{1}{2} (e^{x} + e^{- x})$
- $\sinh x = \frac{1}{2} (e^{x} - e^{- x})$
Therefore they can be related using the identities
- $\cos x \equiv \cosh (i x)$ or $\cosh x \equiv \cos (i x)$
- $\sin x \equiv - isinh (i x)$ or $\sinh x \equiv - isin (i x)$

What are the hyperbolic identities?

In general, the hyperbolic identities are the same as the circular trigonometric identities except where there is a product of an even number of sinh terms, in which case the term changes sign
- e.g. $\cos^{2} x + \sin^{2} x \equiv 1$ but $\cosh^{2} x - \sinh^{2} x \equiv 1$
- This is referred to as Osborn’s Rule
  - This occurs because of the connection with the imaginary number i
All the circular trigonometric identities can be used with hyperbolic functions
The main hyperbolic identities you are likely to need are
- $\cosh^{2} x - \sinh^{2} x \equiv 1$
- $\sinh 2 x \equiv 2 \sinh x \cosh x$
- $\cosh 2 x \equiv \cosh^{2} x + \sinh^{2} x$
  - These are listed in the formulae booklet
Other identities include
- $\cosh 2 x \equiv 2 \cosh^{2} x - 1 \equiv 1 + 2 \sinh^{2} x$
- $\sinh (A \pm B) = \sinh A \cosh B \pm \sinh B \cosh A$
- $\cosh (A \pm B) \equiv \cosh A \cosh B \pm \sinh A \sinh B$
The harmonic identities can also be used with hyperbolic functions
- $a \cosh x \pm b \sinh x = R \cosh (x \pm α)$
- $a \sinh x \pm b \cosh x = R \sinh (x \pm α)$
Hyperbolic identities involving tanhx exist
- They are not normally used as it is easier to use sinhx, coshx and their definitions
- If you do use tanhx identities, be careful with implied or ‘hidden’ products of sinhx (e.g. tanh²x)
You can prove these identities by using the definitions of the hyperbolic functions in terms of e

Do reciprocal hyperbolic functions and identities exist?

Yes! However, It is usually easier to deal with identities and equations involving these in terms of sinhx, coshx and their definitions
$cosech x = \frac{1}{\sinh x} = \frac{2}{e^{x} - e^{- x}}$ (Pronounced “coshec”)
$sech x = \frac{1}{\cosh x} = \frac{2}{e^{x} + e^{- x}}$ (Pronounced “shec”)
$\coth x = \frac{1}{\tanh x} = \frac{\cosh x}{\sinh x} = \frac{e^{2 x} + 1}{e^{2 x} - 1}$ (Pronounced “cough”)

How do I use hyperbolic identities to prove other identities?

Start with the LHS and use the hyperbolic identities to rearrange into the RHS
This approach can lead to what seems like a dead-end
- In such cases simplify the LHS as far as possible, ideally so that it is in terms of sinhx and/or coshx only
- Then use the sinhx and coshx definitions to write the LHS in terms of e
- Repeat this for the RHS so that the LHS and RHS ‘meet in the middle’

How do I solve equations involving hyperbolic functions?

Use identities to create an equation in terms of sinhx or coshx only
- This should be a familiar equation to solve – linear, quadratic, etc
- Find exact answers in terms of natural logarithms
  - Using the inverse hyperbolic functions definitions
- Use your calculator if exact answers are not required
As with circular trigonometric equations, do not cancel hyperbolic terms, rearrange so the equation equals zero and factorise
When solving equations be careful when solving coshx = k (for constant k)
- cosh^-1x is not necessarily the same as arcoshx
  - arcoshx is, strictly speaking, referring to the inverse function of coshx such that coshx is a one-to-one function
- Using the graph you can see that the for k>1 there are two solutions to $\cosh x = k$
  - $x = \pm arcosh k$
  - This can be written in logarithmic form as $\pm \ln (k + \sqrt{k^{2} - 1})$
  - This can be shown to be equivalent to $\ln (k \pm \sqrt{k^{2} - 1})$
- If k=1 then the only solution to $\cosh x = k$ is x=0
- If k<1 then there are no real solutions to $\cosh x = k$

Examiner Tip

You can use the A Level Maths section of the formula booklet to remind you of trigonometric identities (such as sin(A±B)) which you can then adapt for the hyperbolic trig functions – don’t limit yourself to just the Further Maths section

Worked example

Using the definitions of

\sinh x

and

\cosh x

prove the identity

\cosh 2 x = 1 + 2 \sinh^{2} x

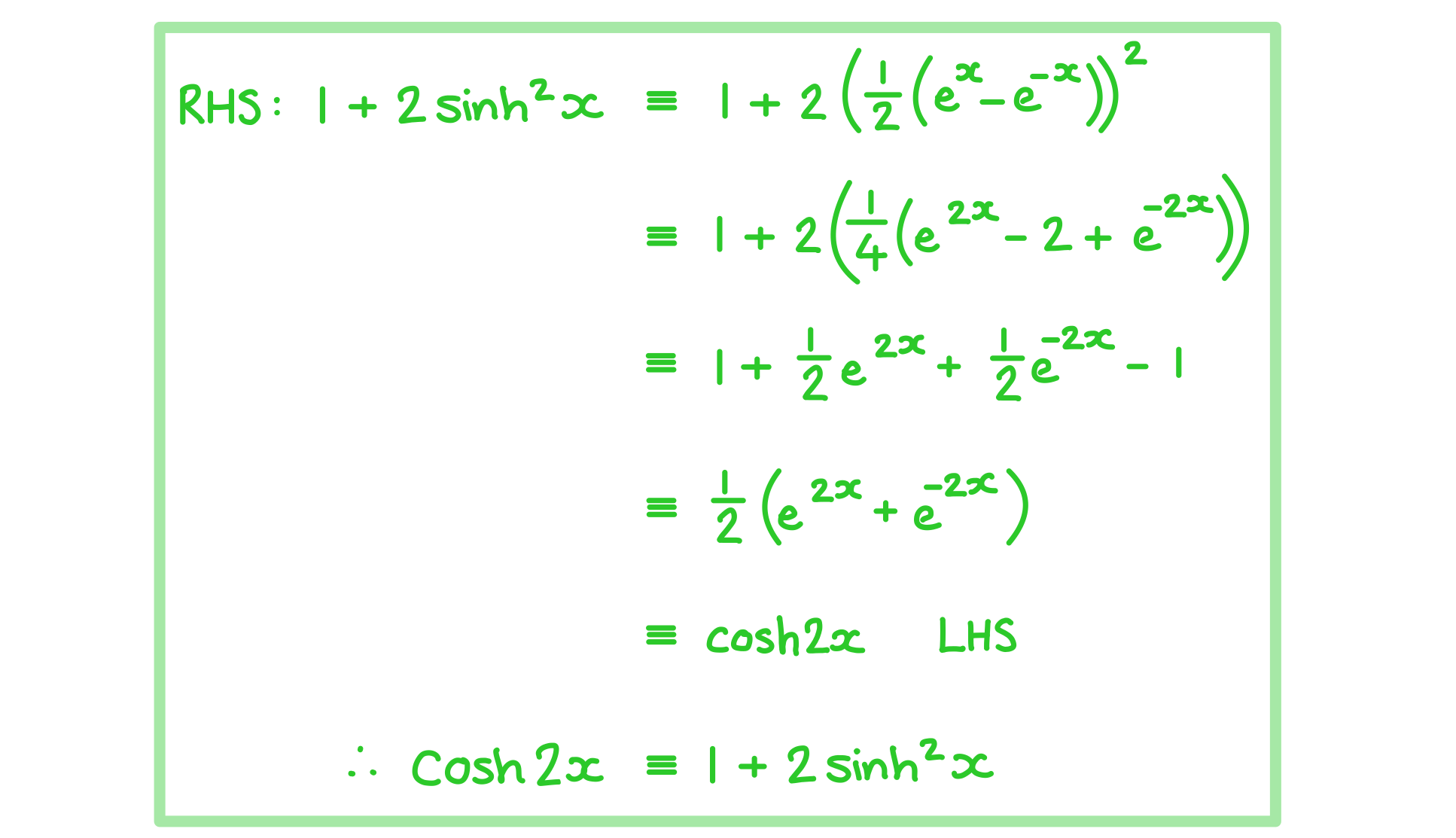
al-fm-4-1-3-we-solution-a

Find the real solutions, as exact values, to the equation

\cosh 2 x = 15 + 3 \sinh x

al-fm-4-1-3-we-solution-b

Hyperbolic Identities & Equations (Edexcel A Level Further Maths: Core Pure)

Revision Note

Are there identities linking the hyperbolic functions to the circular trig functions?

What are the hyperbolic identities?

Do reciprocal hyperbolic functions and identities exist?

How do I use hyperbolic identities to prove other identities?

How do I solve equations involving hyperbolic functions?

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

1. Complex Numbers

1.1 Complex Numbers & Argand Diagrams

1.1.1 Introduction to Complex Numbers

1.1.2 Solving Equations with Complex Roots

1.1.3 Modulus & Argument

1.1.4 Modulus-Argument Form

1.1.5 Loci in Argand Diagrams

1.1.6 Regions in Argand Diagrams

1.2 Exponential Form & de Moivre's Theorem

1.2.1 Exponential Form

1.2.2 de Moivre's Theorem

1.2.3 Applications of de Moivre's Theorem

1.2.4 Roots of Complex Numbers

2. Matrices

2.1 Properties of Matrices

2.1.1 Introduction to Matrices

2.1.2 Determinants of Matrices

2.1.3 Inverses of Matrices

2.2 Transformations using Matrices

2.2.1 Transformations using a Matrix

2.2.2 Geometric Transformations with Matrices

2.2.3 Invariant Points & Lines

3. Further Algebra & Functions

3.1 Roots of Polynomials

3.1.1 Roots of Polynomials

3.1.2 Linear Transformations of Roots

3.2 Series

3.2.1 Sums of Integers, Squares & Cubes

3.2.2 Method of Differences

3.3 Maclaurin Series

3.3.1 Maclaurin Series

4. Hyperbolic Functions

4.1 Hyperbolic Functions

4.1.1 Hyperbolic Functions & Graphs

4.1.2 Logarithmic Forms of Inverse Hyperbolic Functions

4.1.3 Hyperbolic Identities & Equations

4.1.4 Differentiating & Integrating Hyperbolic Functions

5. Further Calculus

5.1 Volumes of Revolution

5.1.1 Volumes of Revolution

5.1.2 Modelling with Volumes of Revolution

5.2 Methods in Calculus

5.2.1 Improper Integrals

5.2.2 Mean Value of a Function

5.2.3 Integrating with Partial Fractions

5.2.4 Calculus involving Inverse Trig

5.2.5 Integration by Substitution

6. Further Vectors

6.1 Vector Lines

6.1.1 Equations of Lines in 3D

6.1.2 Pairs of Lines in 3D

6.1.3 Angle between Lines

6.1.4 Shortest Distances - Lines

6.2 Vector Planes

6.2.1 Equations of planes

6.2.2 Combinations of Lines & Planes

6.2.3 Combinations of Planes

6.2.4 Shortest Distances - Planes

7. Polar Coordinates

7.1 Polar Coordinates

7.1.1 Polar Coordinates

7.1.2 Calculus with Polar Coordinates

8. Differential Equations

8.1 First Order Differential Equations

8.1.1 Intro to Differential Equations

8.1.2 Solving First Order Differential Equations

8.1.3 Modelling using First Order Differential Equations

8.2 Second Order Differential Equations

8.2.1 Solving Second Order Differential Equations

8.2.2 Coupled First Order Linear Equations