Revision NotesExam QuestionsPast Papers
A LevelFurther MathsEdexcelCore PureRevision NotesHyperbolic FunctionsHyperbolic FunctionsLogarithmic Forms of Inverse Hyperbolic Functions

Logarithmic Forms of Inverse Hyperbolic Functions (Edexcel A Level Further Maths) : Revision Note

Paul

Author

Paul

Last updated

Logarithmic Forms of Inverse Hyperbolic Functions

What are the definitions of the inverse hyperbolic functions?

  • arsinh x equals ln open parentheses x plus square root of x squared plus 1 end root close parentheses, x element of straight real numbers

  • ar cosh x equals ln open parentheses x plus square root of x squared minus 1 end root close parentheses, x greater or equal than 1

    • Since coshx is a many-to-one function, its domain is restricted to x ≥ 0 when finding the inverse

    • Therefore, its range is coshx ≥ 1

    • So, the domain of the inverse function is x ≥ 1

  • artanh x equals 1 half ln open parentheses fraction numerator 1 plus x over denominator 1 minus x end fraction close parentheses, vertical line x vertical line less than 1

  • These three definitions are in the formula booklet

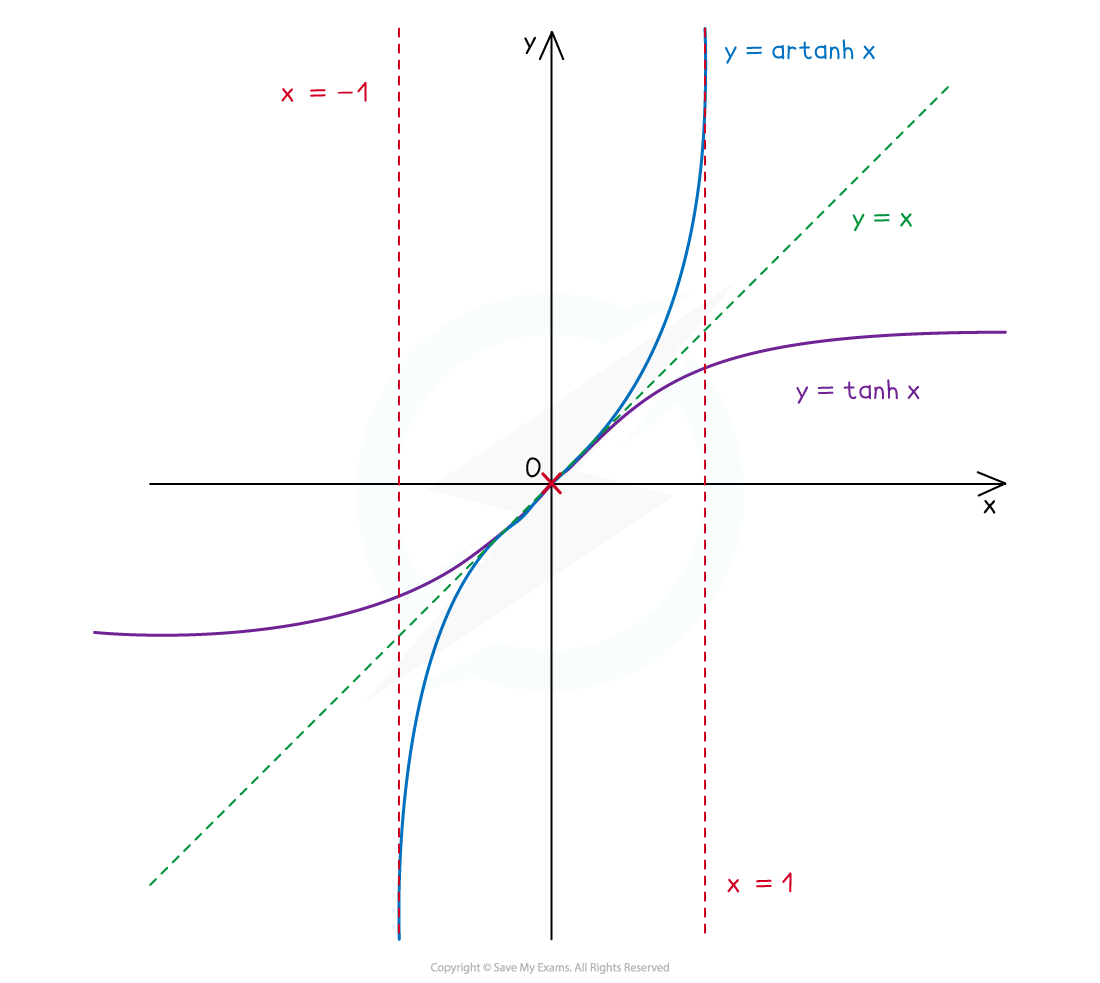
What are the graphs of the inverse hyperbolic functions and their key features?

  • As they are inverse functions, they are reflections of their original functions in the line y=x

  • space y equals arsinh x

    • Domain: x element of straight real numbers

    • Range: space y element of straight real numbers

edexcel-al-fm-cp-4-1-2-arsinhx-graph

  • space y equals ar cosh x

    • Domain: x greater or equal than 1

    • Range: space y greater or equal than 0

edexcel-al-fm-cp-4-1-2-arcoshx-graph

  • space y equals ar tanh x

    • Domain: negative 1 less than x less than 1

    • Range: space y element of straight real numbers

edexcel-al-fm-cp-4-1-2-artanhx-graph

How do I derive the logarithmic formulae for the inverse hyperbolic functions?

  • You need to be able to derive each inverse from the definition of the original

  • STEP 1

    Write in terms of e

    • space y equals arsinh x and rearrange to x equals sinh y

    • x equals 1 half open parentheses straight e to the power of y minus straight e to the power of negative y end exponent close parentheses

  • STEP 2

    Form a quadratic in terms of ey

    • Multiply by 2ey and rearrange

    • open parentheses straight e to the power of y close parentheses squared minus 2 x straight e to the power of y minus 1 equals 0

  • STEP 3

    Solve the quadratic and find an expression for y

    • straight e to the power of y equals x plus-or-minus square root of x squared plus 1 end root

      • Reject x minus square root of x squared plus 1 end root as this produces negative values as square root of x squared plus 1 end root greater than x whereas straight e to the power of y greater than 0

    • space y equals ln open parentheses x plus square root of x squared plus 1 end root close parentheses

  • The derivations of the other two formulae are similar

    • For arcosh x both ln open parentheses x plus square root of x squared minus 1 end root close parentheses and ln open parentheses x minus square root of x squared minus 1 end root close parentheses are well-defined for x greater or equal than 1 

      • We choose arcosh x equals ln open parentheses x plus square root of x squared minus 1 end root close parentheses as arcosh x greater or equal than 0 and it can be shown that ln open parentheses x minus square root of x squared minus 1 end root close parentheses equals ln open parentheses fraction numerator 1 over denominator x plus square root of x squared minus 1 end root end fraction close parentheses equals negative ln open parentheses x plus square root of x squared minus 1 end root close parentheses

Examiner Tips and Tricks

  • Be careful when working with the circular (“normal”) inverse trig functions and the inverse hyperbolic functions

    • Only the “ar” denotes inverse

      • The “c” in arcsin x, arccos x, arctan x indicates the circular functions

      • The hyperbolic functions have “h”, but the “h” doesn’t come immediately after the “ar”: arsinh x, arcosh x, artanh x

    • Be careful not to confuse these, especially when looking them up in the formulae booklet

Worked Example

Starting from the definition of tanh x, show that 

artanh x equals 1 half ln open parentheses fraction numerator 1 plus x over denominator 1 minus x end fraction close parentheses when vertical line x vertical line less than 1.

al-fm-4-1-2-we-solution

 

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Hyperbolic Functions & GraphsNext:Hyperbolic Identities & Equations
    Paul

    Author: Paul

    Expertise: Maths Content Creator (Previous)

    Paul has taught mathematics for 20 years and has been an examiner for Edexcel for over a decade. GCSE, A level, pure, mechanics, statistics, discrete – if it’s in a Maths exam, Paul will know about it. Paul is a passionate fan of clear and colourful notes with fascinating diagrams.