A LevelFurther Maths: Core PureEdexcelRevision Notes2. Matrices2.1 Properties of Matrices2.1.2 Determinants of Matrices

Determinants of Matrices (Edexcel A Level Further Maths: Core Pure)

Revision Note

Test yourself
Naomi C

Author

Naomi C

Last updated

Determinant of a 2x2 Matrix

What is a determinant?

  • The determinant is a numerical value (positive or negative) calculated from the elements in a matrix and is used to find the inverse of a matrix
  • You can only find the determinant of a square matrix
  • The method for finding the determinant of a 2 cross times 2 matrix is given by: 

bold italic A equals open parentheses table row a b row c d end table close parentheses rightwards double arrow det space bold italic A equals open vertical bar bold italic A close vertical bar equals a d minus b c

Worked example

Consider the matrix bold italic A equals open parentheses table row 3 cell negative 6 end cell row p 7 end table close parentheses, where p element of straight real numbers is a constant. Given that det space bold italic A equals negative 3, find the value of p.

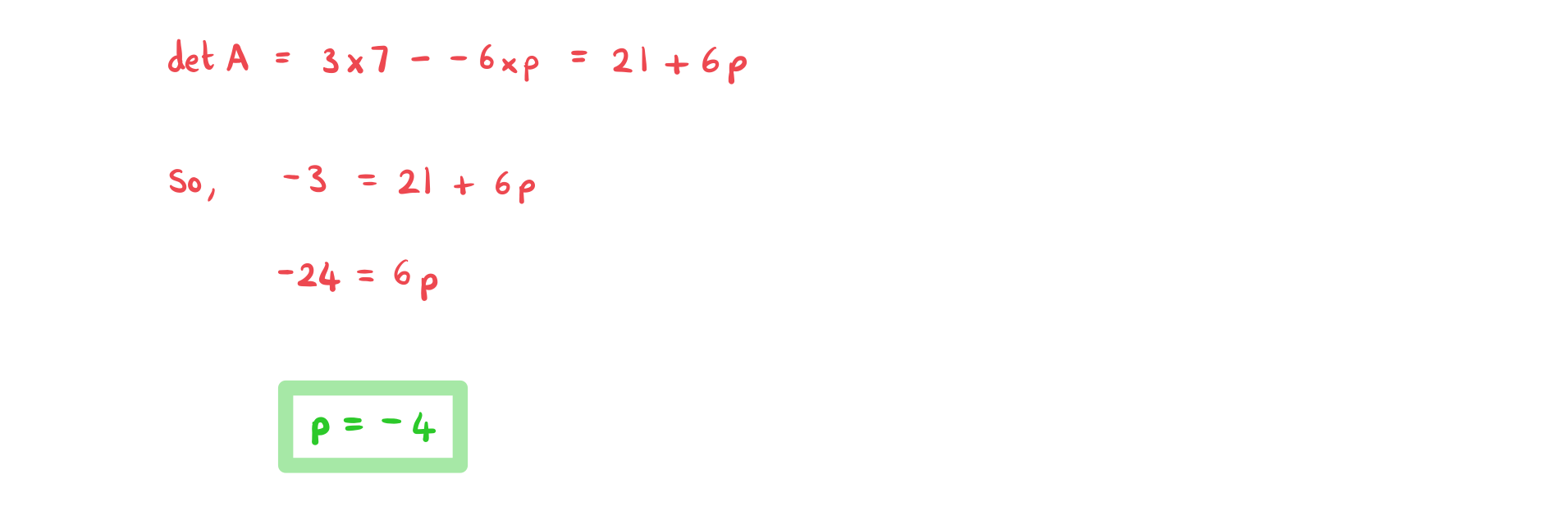
rn-1-7-matrices

Determinant of a 3x3 Matrix

What is the minor  of an element in a 3x3 matrix?

  • For any element in a 3x3 matrix, the minor is the determinant of the 2x2 matrix created by crossing out the row and column containing that element
  • For the matrix open parentheses table row a b c row d e f row g h i end table close parentheses
    • The minor of the element a would be found by:
      • crossing out the first row and first column open parentheses table row cell vertical horizontal strike horizontal strike a end strike end cell cell horizontal strike b end cell cell horizontal strike c end cell row cell vertical strike d end cell e f row cell vertical strike g end cell h i end table close parentheses 
      • finding the determinant of the remaining 2x2 matrix open vertical bar table row e f row h i end table close vertical bar equals e i minus f h
    • The minor of the element f would be found by:
      • crossing out the second row and third column open parentheses table row a b cell vertical strike c end cell row cell horizontal strike d end cell cell horizontal strike e end cell cell vertical horizontal strike f end cell row g h cell vertical strike i end cell end table close parentheses
      • finding the determinant of the remaining 2x2 matrix open vertical bar table row a b row g h end table close vertical bar equals a h minus b g

How do I find the determinant of a 3x3 matrix?

  • Finding the determinant of a 3x3 matrix is best explained using an example
  • STEP 1
    Select any row or column in the matrix
    • e.g.  Selecting Row 2 of bold italic M equals open parentheses table row 4 cell negative 2 end cell 3 row 5 6 cell negative 7 end cell row cell negative 8 end cell 2 cell negative 1 end cell end table close parentheses
  • STEP 2
    Use the matrix of signs open parentheses table row plus minus plus row minus plus minus row plus minus plus end table close parentheses to find the row or column that corresponds to the row or column selected in Step 1
    • e.g. open parentheses table row plus minus plus row minus plus minus row plus minus plus end table close parentheses Row 2 was selected so “-  +  -“ will be needed
  • STEP 3
    Multiply each element in the selected row or column by its minor and use the corresponding signs form the matrix of signs to determine whether to add or subtract each product
    • e.g. det bold italic M equals negative left parenthesis 5 right parenthesis open vertical bar table row cell negative 2 end cell 3 row 2 cell negative 1 end cell end table close vertical bar plus left parenthesis 6 right parenthesis open vertical bar table row 4 3 row cell negative 8 end cell cell negative 1 end cell end table close vertical bar minus left parenthesis negative 7 right parenthesis open vertical bar table row 4 cell negative 2 end cell row cell negative 8 end cell 2 end table close vertical bar
  • STEP 4
    Evaluate the minors and calculate the determinant
    • e.g. det bold italic M equals negative left parenthesis 5 right parenthesis left parenthesis negative 4 right parenthesis plus left parenthesis 6 right parenthesis left parenthesis 20 right parenthesis minus left parenthesis negative 7 right parenthesis left parenthesis negative 8 right parenthesis equals 84
    • Check the answer using a calculator with a matrix feature

Examiner Tip

  • In general, you can use the top row to find the determinant
    • this will save having to recall the matrix of signs, it will always be “+ -  +”
    • and allow you to quickly jump from Step 1 to Step 4 in the method above
    • the matrix of signs is still needed for finding the inverse of a 3x3 matrix
  • Using a row or column that contains a 0 can speed up the process
  • Do use the matrix mode on your calculator where possible
    • Look for any notes on questions about using/not using “calculator technology”
    • Consider the number of marks a question or part is worth

Worked example

Let bold italic M equals open parentheses table row 2 cell negative 4 end cell 5 row 2 cell 2 k squared end cell cell negative k end cell row k cell k plus 1 end cell cell k squared end cell end table close parentheses where k is a positive integer.

a)
Find, in terms of k, the determinant of M.tuqfYHxG_rn-2-1-properties-of-matrices
b)
Given that det bold italic M equals 226, find the value of k.

 determinant-of-a-3-by-3-matrix-part-b

Properties of Determinants

What are the properties of determinants of matrices?

  • The determinant of an identity matrix is det space left parenthesis bold italic I right parenthesis equals 1
  • The determinant of a zero matrix is det space left parenthesis bold italic O right parenthesis equals 0
  • When finding the determinant of a multiple of a matrix or the product of two matrices:
    • det space left parenthesis k bold italic A right parenthesis equals k to the power of n space det space left parenthesis bold italic A right parenthesis(for a n cross times n matrix)
    • det space left parenthesis bold italic A bold italic B right parenthesis equals det space left parenthesis bold italic A right parenthesis cross times det space left parenthesis bold italic B right parenthesis
    • det open parentheses bold italic A to the power of bold minus bold 1 end exponent close parentheses equals fraction numerator 1 over denominator det open parentheses bold italic A close parentheses end fraction
  • If space det space left parenthesis bold italic A right parenthesis equals 0 then A is singular
  • If space det space left parenthesis bold italic A right parenthesis not equal to 0 then A is non-singular

Worked example

Consider the matrix bold italic A equals open parentheses table row 3 cell negative 6 end cell row p 7 end table close parentheses, where p element of straight real numbers is a constant. Given that det space bold italic A equals negative 3, find the determinant of 4 bold italic A.

1-7-3-ib-ai-hl-determinants--inverses-we-1b

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfNext topic

    Did this page help you?

    Naomi C

    Author: Naomi C

    Expertise: Maths

    Naomi graduated from Durham University in 2007 with a Masters degree in Civil Engineering. She has taught Mathematics in the UK, Malaysia and Switzerland covering GCSE, IGCSE, A-Level and IB. She particularly enjoys applying Mathematics to real life and endeavours to bring creativity to the content she creates.